Построение линейной парной регрессии. Построение модели парной регрессии. По территориям Центрального района известны данные за 1995 г
 Скачать 74.84 Kb. Скачать 74.84 Kb.
|
|
Решение 1. Для построения линейного уравнения множественной регрессии рассчитаем параметры уравнения по формулам: 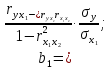 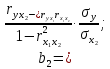 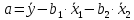 Среднеквадратические отклонения определим по формулам: 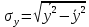 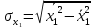 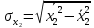 Рассчитаем средние величины по формулам: 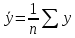 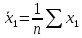 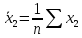 Представим полученные результаты в расчетной таблице 3: Таблица 3. Расчетная таблица
Парные линейные коэффициенты ( 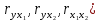 рассчитаем по формулам: рассчитаем по формулам: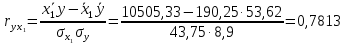 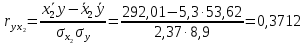 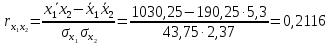 Вычислим параметры уравнения множественной регрессии: 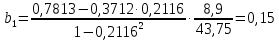 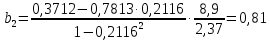 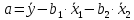 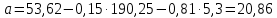 Таким образом, получили линейное уравнение множественной регрессии, выражающее зависимость цены продажи объекта недвижимости города у от общей площади 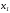 и рейтинга бытовых условий и рейтинга бытовых условий 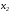 : :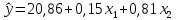 Анализ коэффициентов уравнения множественной регрессии приводит к выводу об уровне влияния каждого их факторов на показатель цены продажи объекта недвижимости. Параметр 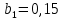 показывает, что с увеличением общей площади на 1 процентный пункт ожидается увеличение цены продажи объекта недвижимости на 0,15 тыс.$. Увеличение же рейтинга бытовых условий на 1 процентный пункт приведет к росту цены продажи объекта недвижимости на 0,81 тыс.$. Отсюда можно сделать соответствующие практические выводы для осуществления мероприятий, направленных на повышение цены продажи объекта недвижимости. показывает, что с увеличением общей площади на 1 процентный пункт ожидается увеличение цены продажи объекта недвижимости на 0,15 тыс.$. Увеличение же рейтинга бытовых условий на 1 процентный пункт приведет к росту цены продажи объекта недвижимости на 0,81 тыс.$. Отсюда можно сделать соответствующие практические выводы для осуществления мероприятий, направленных на повышение цены продажи объекта недвижимости.2. Средние частные коэффициенты эластичности 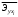 показывают, на сколько процентов от значения своей средней показывают, на сколько процентов от значения своей средней 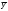 изменяется результат при изменении фактора изменяется результат при изменении фактора 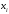 на 1% от своей средней на 1% от своей средней 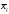 и при фиксированном воздействии на и при фиксированном воздействии на 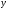 всех прочих факторов, включенных в уравнение регрессии. всех прочих факторов, включенных в уравнение регрессии.Средние коэффициенты эластичности для каждого фактора вычислим по формуле: 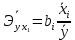 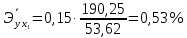 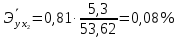 С увеличением общей площади 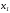 на 1% от его среднего уровня цена продажи объекта недвижимости возрастет на 0,53% от своего среднего уровня; при повышении рейтинга бытовых условий на 1% от его среднего уровня цена продажи объекта недвижимости возрастет на 0,53% от своего среднего уровня; при повышении рейтинга бытовых условий 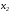 на 1% цена продажи у увеличивается только на 0,08% от своего среднего уровня. По значениям частных коэффициентов эластичности можно сделать вывод о более сильной степени влияния на результат у признака фактора на 1% цена продажи у увеличивается только на 0,08% от своего среднего уровня. По значениям частных коэффициентов эластичности можно сделать вывод о более сильной степени влияния на результат у признака фактора 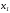 , чем признака фактора , чем признака фактора 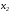 : 0,53% против 0,08%. : 0,53% против 0,08%.3. Связь стандартизованных коэффициентов 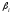 с коэффициентами множественной регрессии с коэффициентами множественной регрессии 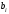 описывается формулой описывается формулой 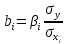 , из которой следует: , из которой следует: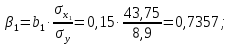 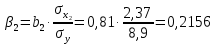 Анализ 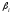 показывает, что на цену продажи наибольшее влияние из двух исследуемых факторов с учетом уровня их вариации способен оказать фактор показывает, что на цену продажи наибольшее влияние из двух исследуемых факторов с учетом уровня их вариации способен оказать фактор 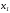 - общая площадь, так как он имеет наибольшее (по абсолютной величине) значение - общая площадь, так как он имеет наибольшее (по абсолютной величине) значение 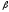 -коэффициента. -коэффициента.4. Расчет линейных коэффициентов парной корреляции определяет тесноту попарно связанных переменных, использованных в данном уравнении множественной регрессии. Парные коэффициенты вычислены нами ранее: 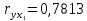 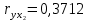 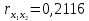 Линейные коэффициенты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии. Рассчитаем частные коэффициенты корреляции по формулам: 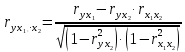 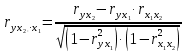 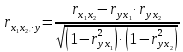 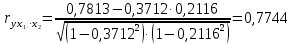 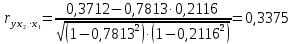 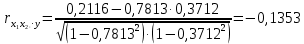 Полученные значения коэффициентов парной корреляции свидетельствуют о тесной связи цены продажи у с общей площадью 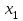 , и о средней связи с рейтингом бытовых условий , и о средней связи с рейтингом бытовых условий 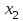 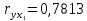 и и 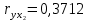 . .В то же время межфакторная связь 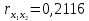 практически отсутствует. практически отсутствует. Коэффициенты частной корреляции дают более точную характеристику тесноты связи двух признаков, по сравнению с коэффициентами парной корреляции, так как очищают парную зависимость от взаимодействия данной пары признаков с другими признаками, представленными в модели. Наиболее тесно связаны у и 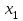 : : 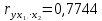 связь у и связь у и 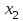 гораздо слабее: гораздо слабее: 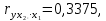 а межфакторная зависимость а межфакторная зависимость 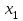 и и 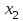 ниже, чем парная ниже, чем парная 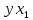 и и 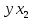 : : 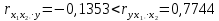 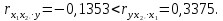 В итоге отсутствует необходимость исключить фактор 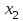 - рейтинг бытовых условий – из правой части уравнения множественной регрессии. - рейтинг бытовых условий – из правой части уравнения множественной регрессии.Сравнивая коэффициенты парной и частной корреляции, можно увидеть, что из-за высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные оценки тесноты связи: 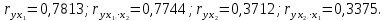 Именно по этой причине рекомендуется при наличии сильной коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота межфакторной зависимости. Индекс множественной корреляции может вычислим с помощью стандартизованных коэффициентов по формуле: 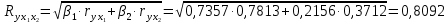 Индекс множественной корреляции измеряет одновременное влияние факторных признаков на результативный. 5. Коэффициент множественной детерминации рассчитаем по формуле как квадрат индекса множественной корреляции: 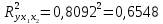 Коэффициент множественной детерминации оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 65,5% и указывает на среднюю степень обусловленности вариации результата вариацией факторов, другими словами - среднюю связь факторов с результатом. Оценим надежность уравнения регрессии в целом и показателя тесноты связи 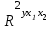 с помощью F-критерия Фишера, который определим по формуле: с помощью F-критерия Фишера, который определим по формуле: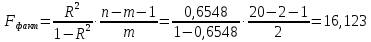 Анализ выполним, сравнивая фактическое и табличное (критическое) значение F-критерия Фишера. 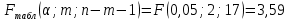 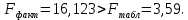 Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения множественной регрессии и показателя тесноты связи 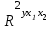 . . |