Построение линейной парной регрессии. Построение модели парной регрессии. По территориям Центрального района известны данные за 1995 г

• Название: По территориям Центрального района известны данные за 1995 г
• Анкор: Построение линейной парной регрессии
• Дата: 02.11.2021
• Размер: 74.84 Kb.
• Имя файла: Построение модели парной регрессии.docx
• Тип: Документы; #261664
• страница: 3 из 3

Задание 3

1. 
   Применив необходимое и достаточное условия идентификации, определить, идентифицировано ли каждое из уравнений модели.
   
2. 
   Сделать вывод об идентифицируемости модели в целом.
   
3. 
   Определить метод оценки параметров модели.
   
4. 
   Записать приведенную форму модели.
   

Модель Менгеса: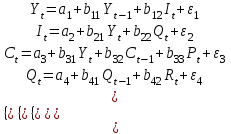



где Y - национальный доход; С - расходы на личное потребление; I - чистые инвестиции; Q - валовая прибыль экономики; Р - индекс стоимости жизни; R- объем продукции промышленности; t - текущий период; t-1 - предыдущий период.

Решение

1. 
   Модель представляет является системой взаимосвязанных (одновременных) уравнений. Проверим каждое ее уравнение на идентификацию.
   

Необходимое условие идентификации – выполнение счетного правила:

D +1 = H – уравнение идентифицируемо;

D +1 < H – уравнение неидентифицируемо;

D +1 > H – уравнение сверхидентифицируемо,

где H – число эндогенных переменных в уравнении;

D– число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.
Эндогенные переменные – взаимосвязанные переменные, которые определяются внутри модели (системы) у.

Экзогенные переменные – независимые переменные, которые определяются вне системы х.

Предопределенные переменные – экзогенные и лаговые (за предыдущие моменты времени) эндогенные переменные системы.

Коэффициенты a и b при переменных – структурные коэффициенты модели.

В данную модель включены четыре эндоге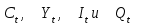нные переменные:

( ) и пять преопределенных переменных (две экзогенные переменные – P_tи R_t и три лаговые эндогенные переменные –

Y_t-1, C_t-1 и Q_t-1).

Проверим необходимое условие идентификации для уравнений модели.

I-е уравнение.

Это уравнение включает в себя две эндогенные переменные (Y_tи I_t) и одну преопределенную переменную (Y_t-1). Таким образом, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 4+1>2. Уравнение сверхидентифицировано.

II-е уравнение.

Это уравнение включает в себя три эндогенные переменные (Q_t, Y_tи I_t) и ноль преопределенных переменных. Таким образом, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 5+1>3. Уравнение сверхидентифицировано.

III-е уравнение.

Это уравнение включает в себя две эндогенные переменные (C_t и Y_t) и две преопределенные переменные (P_tи C_t-1). Таким образом, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 3+1>1. Уравнение сверхидентифицировано.

IV-е уравнение.

Это уравнение включает одну эндогенную переменную (Q_t) и две преопределенных переменных (R_tи Q_t-1). Таким образом, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 3+1> 1. Уравнение сверхидентифицировано.

Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели.

	Yt	Yt-1	It	Qt	Ct	Ct-1	Pt	Qt-1	Rt
I уравнение	-1	b11	b12	0	0	0	0	0	0
II уравнение	b21	0	-1	b22	0	0	0	0	0
III уравнение	b31	0	0	0	-1	b32	b33	0	0
IV уравнение	0	0	0	-1	0	0	0	b41	b42

В соответствии с достаточным условием идентификации определитель матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть равен числу эндогенных переменных модели минус 1, т.е. 4-1=3.

I-е уравнение.

Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид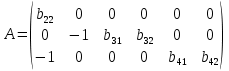



Ее ранг равен 3, так как определитель квадратной подматрицы 3х3 этой матрицы не равен нулю: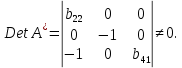


Достаточное условие идентификации для первого уравнения выполняется.
II-е уравнение.

Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид

	Yt	Yt-1	It	Qt	Ct	Ct-1	Pt	Qt-1	Rt
I уравнение	-1	b11	b12	0	0	0	0	0	0
II уравнение	b21	0	-1	b22	0	0	0	0	0
III уравнение	0	0	0	0	-1	b32	b33	0	0
IV уравнение	0	0	0	-1	0	0	0	b41	b42

.
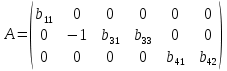Ее ранг равен 3, так как определитель квадратной подматрицы 3х3 этой матрицы не равен нулю: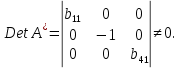


Достаточное условие идентификации для второго уравнения выполняется.
III-е уравнение.

Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид

	Yt	Yt-1	It	Qt	Ct	Ct-1	Pt	Qt-1	Rt
I уравнение	-1	b11	b12	0	0	0	0	0	0
II уравнение	b21	0	-1	b22	0	0	0	0	0
III уравнение	0	0	0	0	-1	b32	b33	0	0
IV уравнение	0	0	0	-1	0	0	0	b41	b42

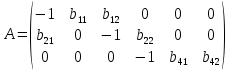Ее ранг равен 3, так как определитель квадратной подматрицы 3х3 этой матрицы не равен нулю: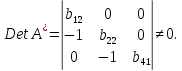


Достаточное условие идентификации для третьего уравнения выполняется.
IV-е уравнение.

Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид

	Yt	Yt-1	It	Qt	Ct	Ct-1	Pt	Qt-1	Rt
I уравнение	-1	b11	b12	0	0	0	0	0	0
II уравнение	b21	0	-1	b22	0	0	0	0	0
III уравнение	0	0	0	0	-1	b32	b33	0	0
IV уравнение	0	0	0	-1	0	0	0	b41	b42

.

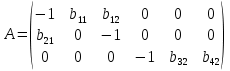Ее ранг равен 3, так как определитель квадратной подматрицы 3х3 этой матрицы не равен нулю: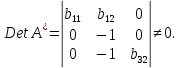


Достаточное условие идентификации для четвертого уравнения выполняется.

Таким образом, все уравнения модели сверхидентифицированы.

Так как уравнения сверхидентифицированы, то для оценки параметров уравнений можно применить двухшаговый МНК.

2. Приведенная форма модели – это система линейных функций эндогенных переменных от всех предопределенных переменных системы: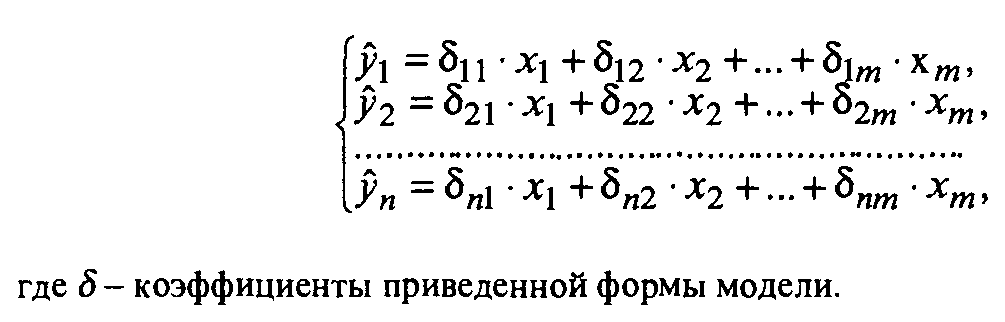



Запишем приведенную форму заданной модели в общем виде: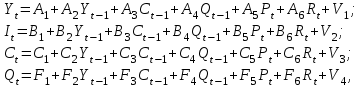



где V₁, V₂, V₃ и V₄ – случайные ошибки.