курсовая. Подпись ответственного за регистрацию. Курсовая работа формирование структуры стандарта на продукцию тесто для хлебобублочных изделий и построение сетевого графика разработки
 Скачать 0.69 Mb. Скачать 0.69 Mb.
|
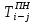 - позднее начало работ - позднее начало работ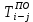 -позднее окончание работ -позднее окончание работ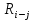 - общий резерв времени - общий резерв времени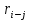 -частный резерв времени -частный резерв времени Ранее начало работ - самый ранний из возможных сроков начала работы, который обусловлен выполнением всех предшествующих работ 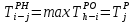 (2.1) (2.1) где 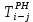 - ранее начало работ; - ранее начало работ;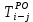 - ранее окончание работ. - ранее окончание работ.Например, 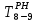 =12 =12Ранее окончание работ- время окончания работы, если она начата в ранний срок. 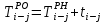 (2.2) (2.2)где 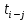 - продолжительность работы; - продолжительность работы;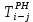 - ранее начало работ; - ранее начало работ;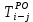 - ранее окончание работ. - ранее окончание работ.Например, 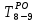 =12+1=13 =12+1=13 (2.3) Критическим путем сетевого графика называют полный путь от исходного до завершающего события, имеющий наибольшую длину (продолжительность) из всех полных путей 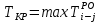  (2.4) Позднее окончание работ - самый поздний допустимый срок окончания работы, при котором планируемы срок достижения цели не меняется. 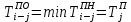 где 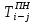 - позднее начало работ; - позднее начало работ;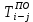 -позднее окончание работ. -позднее окончание работ.Например, 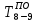 =13 =13 (2.5) Позднее начало работ – самое позднее время начала работы, которое не вызовет задержки окончания ремонта объекта. 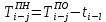 где 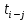 - продолжительность работы; - продолжительность работы;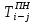 - позднее начало работ; - позднее начало работ;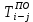 -позднее окончание работ. -позднее окончание работ.Например, 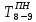 =13-1=12 =13-1=12 (2.6) Общий резерв времени - максимальное количество времени. на которое можно отдалить окончание данной работы, за счет увеличения продолжительности или задержки ее начала не изменяя срока достижения конечной цели. 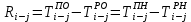 где 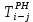 - ранее начало работ; - ранее начало работ;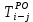 - ранее окончание работ; - ранее окончание работ;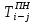 - позднее начало работ; - позднее начало работ;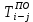 -позднее окончание работ; -позднее окончание работ;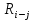 - общий резерв времени. - общий резерв времени.Например, 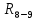 =0 =0Частный резерв времени -максимальное количество времени, на которое можно отдалить окончание данной работы, за счет увеличения продолжения или задержки срока ее начала не изменился.  (2.7) 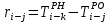 где 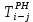 - ранее начало работ; - ранее начало работ;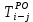 - ранее окончание работ; - ранее окончание работ;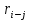 -частный резерв времени. -частный резерв времени.Например, 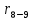 =0 =0Таблица 2.1 - Расчет резерва событий
Заполнение таблицы 2.2. Перечень работ и их продолжительность перенесем во вторую и третью графы. При этом работы следует записывать в графу 2 последовательно: сначала начиная с номера 0, затем с номера 1 и т.д. Во второй графе поставим число, характеризующее количество непосредственно предшествующих работ (КПР) тому событию, с которого начинается рассматриваемая работа. Так, для работы (1,2) в графу 1 поставим число 1, т.к. на номер 1 оканчиваются 1 работы: (0,1). Графу 4 получаем из таблицы 2.2 (tp(i)). Графу 7 получаем из таблицы 2.2 (tп(i)). Значения в графе 5 получаются в результате суммирования граф 3 и 4. В графе 6 позднее начало работы определяется как разность позднего окончания этих работ и их продолжительности (из значений графы 7 вычитаются данные графы 3); Содержимое графы 8 (полный резерв времени R(ij)) равно разности граф 6 и 4 или граф 7 и 5. Если R(ij) = 0, то работа является критической Полный резерв пути показывает, на сколько в сумме может быть увеличена продолжительность всех работ, принадлежащих данному пути, при условии, что срок выполнения всего комплекса работ не изменится. Образовывается, когда предшествующие работы закончатся в свой наиболее ранний срок. Находим полный резерв RПi-j = Tпj-ti-j-Tрi (2.8) RijП (0,1) = 0-4-0 = -4 RijП (1,2) = 8-2-4 = 2 RijП (1,3) = 0-2-4 = -6 RijП (1,4) = 5-1-4 = 0 RijП (2,5) = 10-2-6 = 2 RijП (3,2) = 0-0-6 = -6 RijП (3,6) = 7-0-6 = 1 RijП (4,6) = 7-2-5 = 0 RijП (5,7) = 10-0-8 = 2 RijП (6,7) = 10-3-7 = 0 (RijП 7,8) = 12-2-10 = 0 RijП (8,9) = 13-1-12 = 0 RijП (9,10) = 18-5-13 = 0 RijП (9,11) = 17-1-13 = 3 RijП (9,12) = 21-2-13 = 6 RijП (9,13) = 21-3-13 = 5 RijП (10,14) = 21-3-18 = 0 RijП (11,15) = 20-3-14 = 3 RijП (12,16) = 21-0-15 = 6 RijП (13,16) = 21-0-16 = 5 RijП (14,16) = 21-0-21 = 0 RijП (15,16) = 21-1-17 = 3 RijП (16,17) = 25-4-21 = 0 RijП (17,18) = 26-1-25 = 0 RijП (17,19) = 26-1-25 = 0 RijП (18,20) = 28-2-26 = 0 RijП (19,21) = 28-2-26 = 0 RijП (20,22) = 29-1-28 = 0 RijП (21,22) = 29-1-28 = 0 RijП (22,23) = 32-3-29 = 0 RijП (23,24) = 33-1-32 = 0 RijП (24,25) = 37-4-33 = 0 RijП (25,26) = 41-3-37 = 1 RijП (25,27) = 38-1-37 = 0 RijП (26,29) = 41-0-40 = 1 RijП (27,28) = 40-2-38 = 0 RijП (28,29) = 41-1-40 = 0 RijП (29,30) = 42-1-41 = 0 RijП (30,31) = 43-1-42 = 0 RijП (31,32) = 45-2-43 = 0 RijП (32,33) = 46-1-45 = 0 Свободный резерв времени также можно найти и по формуле RCi-j = Tпi-ti-j-Tрi (2.9) RijC (0,1) = 4-4-0 = 0 RijC (1,2) = 6-2-4 = 0 RijC (1,3) = 6-2-4 = 0 RijC (1,4) = 5-1-4 = 0 RijC (2,5) = 8-2-6 = 0 RijC (3,2) = -2-0-6 = -8 RijC (3,6) = 7-0-6 = 1 RijC (4,6) = 7-2-5 = 0 RijC (5,7) = 10-0-8 = 2 RijC (6,7) = 10-3-7 = 0 RijC (7,8) = 12-2-10 = 0 RijC (8,9) = 13-1-12 = 0 RijC (9,10) = 18-5-13 = 0 RijC (9,11) = 14-1-13 = 0 RijC (9,12) = 15-2-13 = 0 RijC (9,13) = 16-3-13 = 0 RijC (10,14) = 21-3-18 = 0 RijC (11,15) = 17-3-14 = 0 RijC (12,16) = 21-0-15 = 6 RijC (13,16) = 21-0-16 = 5 RijC (14,16) = 21-0-21 = 0 RijC (15,16) = 21-1-17 = 3 RijC (16,17) = 25-4-21 = 0 RijC (17,18) = 26-1-25 = 0 RijC (17,19) = 26-1-25 = 0 RijC (18,20) = 28-2-26 = 0 RijC (19,21) = 28-2-26 = 0 RijC (20,22) = 29-1-28 = 0 RijC (21,22) = 29-1-28 = 0 RijC (22,23) = 32-3-29 = 0 RijC (23,24) = 33-1-32 = 0 RijC (24,25) = 37-4-33 = 0 RijC (25,26) = 40-3-37 = 0 RijC (25,27) = 38-1-37 = 0 RijC (26,29) = 41-0-40 = 1 RijC (27,28) = 40-2-38 = 0 RijC (28,29) = 41-1-40 = 0 RijC (29,30) = 42-1-41 = 0 RijC (30,31) = 43-1-42 = 0 RijC (31,32) = 45-2-43 = 0 RijC (32,33) = 46-1-45 = 0 Независимый резерв времени также можно найти и по формуле RНi-j = Tрj-ti-j-Tпi (2.10) RijН (0,1) = 4-4-0 = 0 RijН (1,2) = 6-2-0 = 4 RijН (1,3) = 6-2-0 = 4 RijН (1,4) = 5-1-0 = 4 RijН (2,5) = 8-2-8 = -2 RijН (3,2) = -2-0-0 = -2 RijН (3,6) = 7-0-0 = 7 RijН (4,6) = 7-2-5 = 0 RijН (5,7) = 10-0-10 = 0 RijН (6,7) = 10-3-7 = 0 RijН (7,8) = 12-2-10 = 0 RijН (8,9) = 13-1-12 = 0 RijН (9,10) = 18-5-13 = 0 RijН (9,11) = 14-1-13 = 0 RijН (9,12) = 15-2-13 = 0 RijН (9,13) = 16-3-13 = 0 RijН (10,14) = 21-3-18 = 0 RijН (11,15) = 17-3-17 = -3 RijН (12,16) = 21-0-21 = 0 RijН (13,16) = 21-0-21 = 0 RijН (14,16) = 21-0-21 = 0 RijН (15,16) = 21-1-20 = 0 RijН (16,17) = 25-4-21 = 0 RijН (17,18) = 26-1-25 = 0 RijН (17,19) = 26-1-25 = 0 RijН (18,20) = 28-2-26 = 0 RijН (19,21) = 28-2-26 = 0 RijН (20,22) = 29-1-28 = 0 RijН (21,22) = 29-1-28 = 0 RijН (22,23) = 32-3-29 = 0 RijН (23,24) = 33-1-32 = 0 RijН (24,25) = 37-4-33 = 0 RijН (25,26) = 40-3-37 = 0 RijН (25,27) = 38-1-37 = 0 RijН (26,29) = 41-0-41 = 0 RijН (27,28) = 40-2-38 = 0 RijН (28,29) = 41-1-40 = 0 RijН (29,30) = 42-1-41 = 0 RijН (30,31) = 43-1-42 = 0 RijН (31,32) = 45-2-43 = 0 RijН (32,33) = 46-1-45 = 0 Следует отметить, что кроме полного резерва времени работы, выделяют еще три разновидности резервов. Частный резерв времени первого вида R1 - часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока ее начального события. R1 находится по формуле: R(i,j)= Rп(i,j) - R(i) (2.11) Частный резерв времени второго вида, или свободный резерв времени Rc работы (i,j) представляет собой часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события. Rc находится по формуле: R(i,j)= Rп(i,j) - R(j) (2.12) Значение свободного резерва времени работы указывает на расположение резервов, необходимых для оптимизации. Таблица 2.2 - Анализ сетевой модели по времени
Окончание таблицы 2.2
Независимый резерв времени Rн работы (i,j) - часть полного резерва, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие начинаются в ранние сроки. Rн находится по формуле: R(i,j)= Rп(i,j)- R(i) - R(j) В данном случае имеются несколько критических путей: Критический путь №1: (0,1) (1,4) (4,6) (6,7) (7,8) (8,9) (9,10) (10,14) (14,16)(16,17)(17,18)(18,20)(20,22)(22,23)(23,24)(24,25)(25,27)(27,28)(28,29)(29,30)(30,31)(31,32)(32,33) Критический путь №2: (0,1) (1,4) (4,6) (6,7) (7,8) (8,9) (9,10) (10,14) (14,16)(16,17)(17,19)(19,21)(21,22)(22,23)(23,24)(24,25)(25,27)(27,28)(28,29)(29,30)(30,31)(31,32)(32,33) Продолжительность критического пути: 46 Анализ сетевого графика Сложность сетевого графика оценивается коэффициентом сложности, который определяется по формуле: Kc = npab / ncob (2.13) где Kc – коэффициент сложности сетевого графика; npab – количество работ, ед.; ncob – количество событий, ед. Сетевые графики, имеющие коэффициент сложности от 1,0 до 1,5, являются простыми, от 1,51 до 2,0 – средней сложности, более 2,1 – сложными. Kc = 41 / 34 = 1.21 Поскольку Kc < 1.5, то сетевой график является простым. Расчет календарной продолжительности разработки стандарта предприятия Для расчета календарной продолжительности разработки стандарта было принята дата 02.02.2021. Расчеты производились путем прибавления к принятой дате чисел, полученных в таблице 2.1 из столбцов 4,5,6,7,8,9. Например, 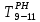 = 02.02.2021+13=15.02.2021 = 02.02.2021+13=15.02.2021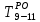 = 02.02.2021+14=16.02.2021 = 02.02.2021+14=16.02.2021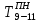 = 02.02.2021+16=18.02.2021 = 02.02.2021+16=18.02.2021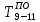 =02.02.2021+17=19.02.2021 =02.02.2021+17=19.02.2021Таблица 2.3 - Календарная продолжительность разработки стандарта
Окончание таблицы 2.3
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
