Детали. Подвижность

• Название: Подвижность
• Дата: 06.02.2018
• Размер: 305.94 Kb.
• Имя файла: Детали.docx
• Тип: Документы; #35911

Содержание

Задание 1……………………………………………………………………..……2

Задание 2…………………………………………………………………...…….11

Задание 3……………………………………………………………………..…..15

Список литературы………………………………………………………………29

Задание 1

Дано

φ=40

а=0.07 м

ω=24 рад/с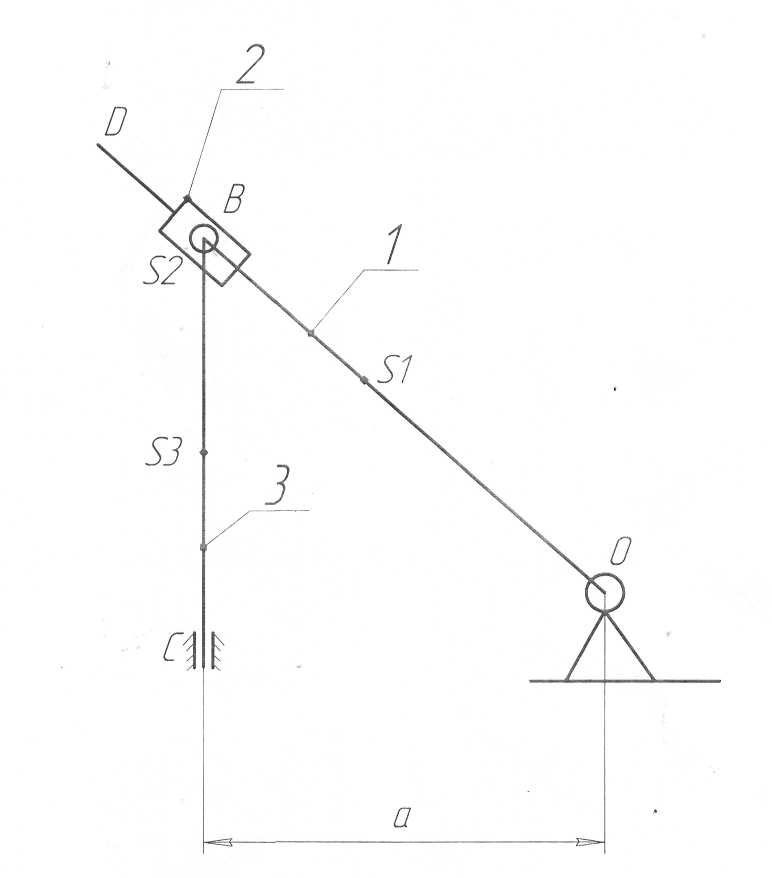

Классифицируем кинематические пары механизма

Таблица 1.1 - Классификация кинематических пар

№ п/п	Номер звеньев, образующих пару	Условное обозначение	Название	Подвижность	Высшая /низшая	Замыкание	Открытая /закрытая
1	0-1	О	Вращательная	1	Н	Г	З
2	1-2		Вращательная	1	Н	Г	З
3	2-3		Поступательная	1	Н	Г	З
4	3-0		Поступательная	1	Н	Г	З

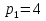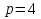Исследуемый механизм состоит только из одноподвижных кинематических пар, поэтому - число одноподвижных кинематических пар в механизме, - общее число кинематических пар в механизме.

Классификация звеньев механизма

Классификация звеньев механизма представлена в таблице 1.2.

Таблица 1.2 - Классификация звеньев

№ п/п	Номер звена	Условное обозначение	Название	Движение	Число вершин (t)
1	0		Стойка	Отсутствует	-
2	1		Кулиса	Вращательное	2
3	3		Кулисный камень	Поступательное	2
4	2		Ползун	Поступательное	2

Находим число присоединений к стойке

Механизм имеет одно (S=1) присоединений к стойке.

Выделяем в простые, элементарные механизмы

В исследуемом сложном механизме можно выделить один элементарный механизм (рис.1.2).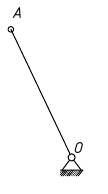



Рис. 1.2. Элементарный механизм

Классифицируем механизм

Исследуемый механизм имеет постоянную структуру, является сложным. Он состоит из одного элементарного механизма и одного стационарных простых.

Определяем подвижность простых механизмов

Анализ движений звеньев механизма и элементов кинематических пар показывает, что и исследуемые простые механизмы, и сам сложный механизм существуют в трёхподвижном пространстве (П=3).

Формулы для определения подвижности этих механизмов примут вид соответственно: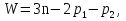

(1.1)

где W – подвижность механизма;

n – число подвижных звеньев механизма;

I – целочисленный индекс;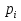

– число кинематических пар i-той подвижности.

.

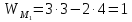Определяем подвижность сложного механизма

Подвижность сложного механизма определяется по формуле: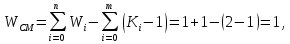



где j – индекс (порядковый номер) общего звена;

m – число звеньев присоединения в механизме;

n – число простых механизмов;

i – индекс (порядковый номер) простого механизма.

Подставив в эти формулы исходные данные 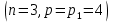, найдем подвижность этого сложного механизма:



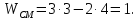Видно, что полученные результаты совпадают.

Проводим классификацию структурных групп по И.И. Артоболевскому

Классификация структурных групп представлена в таблице табл.1.3.

Таблица 1.3 - Классификация структурных групп

№ п/п

Структурная схема

Номер звеньев, образующих группу

Класс,

порядок, вид

1


O

1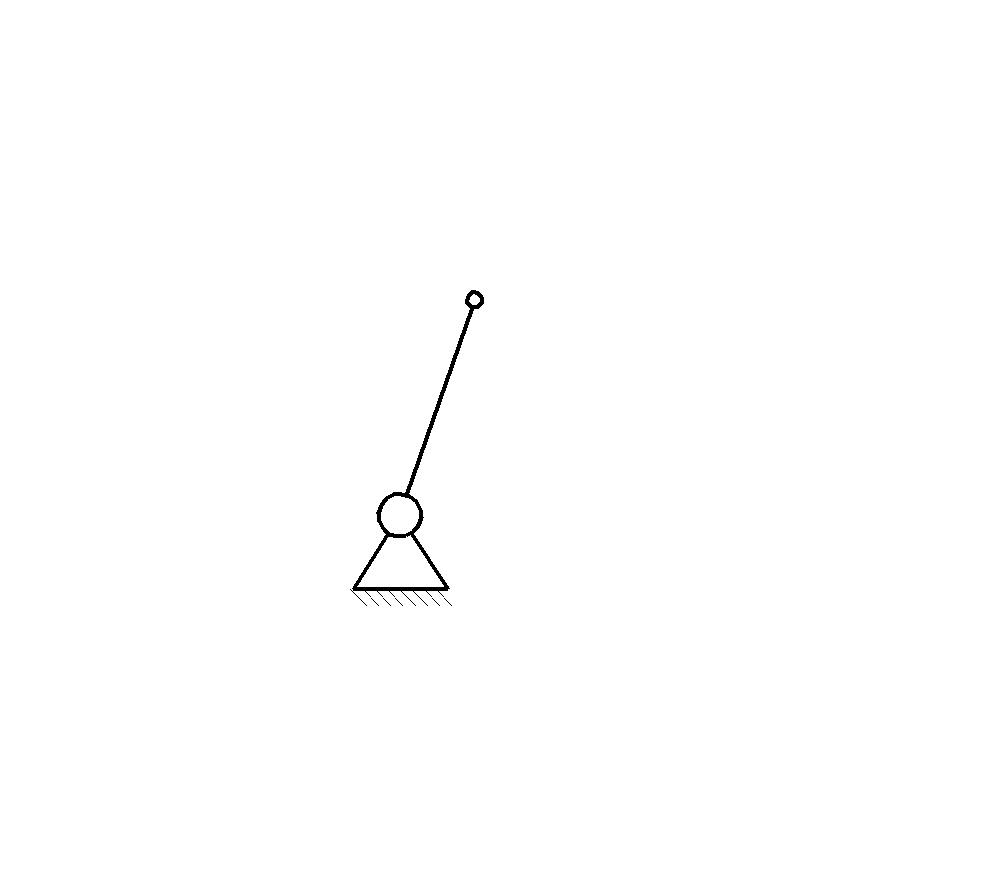


0-1

Механизм I класса

2



2-3

II класс

2 порядок

3-вид

Определяем класс сложного механизма

Механизм относится ко II классу.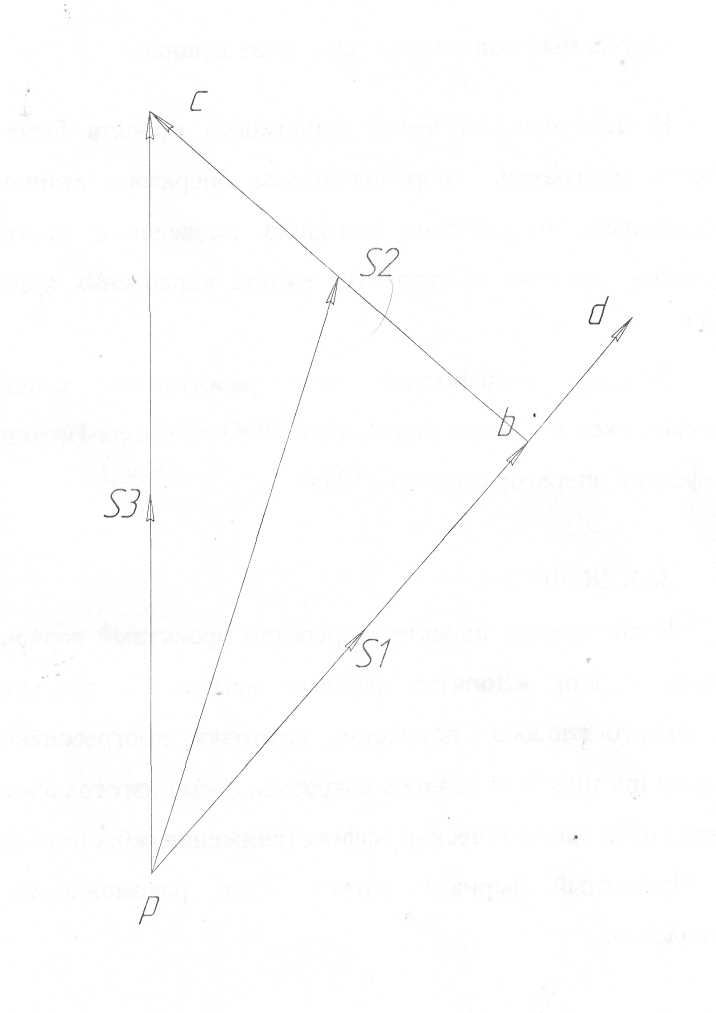




Решение этой задачи графическим методом основано на построении плана скоростей для шестого положения механизма.

План строим следующим образом.

Находим скорость точки А: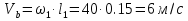

.

Из полюса плана скоростей p – откладываем вектор 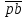= 100 мм, изображающий скорость точки B. Этот вектор перпендикулярен ОB и направлен в сторону вращения звена 1.

Подсчитываем масштабный коэффициент скоростей.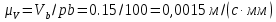

.

Точка B совпадает с точкой А, но принадлежит кулисе 2, которая движется вдоль коромысла CB, вращаясь при этом вместе с ним вокруг точки C. Следовательно: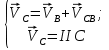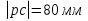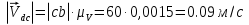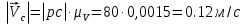



;

;

.

Задание 2

На рис. 2 представлена схема тормозного устройства, состоящего из тормозного барабана 1, тормозных колодок 2,тормозной ленты 3 и рычага 4.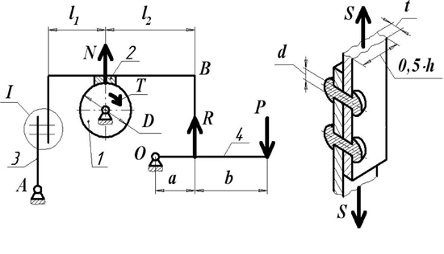


Рис. 2. Расчетная схема тормозного устройства
Требуется:

Рассчитать наибольшее тормозное усилие Р в тормозном устройстве и подобрать размеры поперечного сечения тормозной ленты (h×t,мм), а также количество заклепок на ней. Величина допустимых напряжений среза заклепок [] = 140 МПа, напряжений смятия [] = 320 МПа, напряжений на разрыв ленты []=160МПа. Диаметр заклепки принять равным d = 8 мм, коэффициент трения тормозной колодки о барабан f = 0,30…0,35.

Исходные данные к расчёту:

Величина тормозного момента T = 1000 H·м; диаметра тормозного барабана D=0,1 м. Размеры рычага: а = 0.4 м; b = 1м. Размеры плеч тормоза: 1₁=0,4м; 1₂=0,6м.
Решение задачи:

Необходимую реакцию Η тормозной колодки на барабан определяем по зависимости:

N=2Т/f x D =2 x 1000/0.32 x 0.1=62500Н

где Т - тормозной момент на барабане, Н·м; f - коэффициент трения тормозной колодки о барабан (принимаем равным 0,32); D - диаметр тормозного барабана, м.

Силу натяжения тормозной ленты S и реакцию R тяги рычажной системы определяем при рассмотрении расчётной схемы (рис. 3), составленной на основе расчётной схемы тормозного устройства.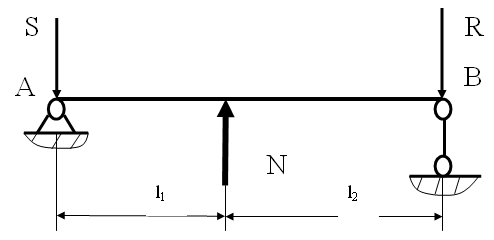


Рис. 3. Расчетная схема
Составим уравнение моментов относительно опоры А (см. рис. 3):

Отсюда:

R=N x l1/l1+l2=62500 x 0.4/1=25000 Н
Составим уравнение моментов относительно опоры В (см. рис 3):

Отсюда:

S=N x l2/l1+l2=62500 x 0.6/1=37500 Н
Для определения необходимого тормозного усилия Р составим уравнение моментов приводного рычага (см. рис. 2):

Отсюда:

Р=R x a /a+b=25000 x 0.4/1.4=7143 Н
Возникающие в заклепочном соединении напряжения среза определим по условию прочности:

где А – площадь поперечного сечения одной заклепки (² );

d – диаметр заклепки, мм (по заданию величина диаметра заклепки известна).

С учетом вышеприведенных формул, получаем:


Тогда необходимое количество заклепок η будет равно:

n= 4S/π x d² x [τ]=4 x 37500/ 3.14х 8 ² х 140=3.7
Количество заклепок n округляем до целого четного числа n = 4.

Используя условие прочности заклепок на смятие, определяем минимальную толщину тормозной ленты t:

Откуда получим:

t= 37500/4 x 320x 8=2.5
Толщину тормозной ленты t округляем до целого числа, t = 3 мм.

Из условия прочности тормозной ленты на разрыв (в сечении с наибольшим количеством заклепок) определяем ширину тормозной ленты h:

где n₃ – количество заклепок в поперечном сечении ленты. Принимаем два ряда заклепок. Тогда: n₃ = n/2 = 4/2 = 2.
h=37500/160 х 3 +2х8=70.3 мм
Ширину тормозной ленты h округляем до целого числа, h = 71 мм.

Задача 3.

На рис. 4 представлена схема электромеханического привода, состоящего из электродвигателя, ременной передачи и одноступенчатого цилиндрического редуктора.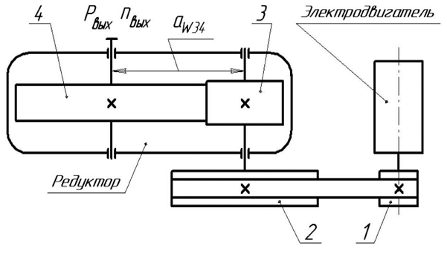


Рис. 4. Смеха привода
Требуется:

1.Выполнить расчет и разработать компоновочный эскиз редуктора.

2.Определить кинематические параметры привода.

3.Определить межосевое расстояние редуктора.

4.Определить геометрические параметры зубчатой передачи.

5.Определить силы, действующие в зубчатом зацеплении.

6.Выполнить предварительный расчет валов.

7.Подобрать подшипники качения.

8.Разработать и выполнить компоновочный эскиз редуктора.

Исходные данные к расчету:

Мощность на выходном валу привода Р_вых = 1,1 кВт; частота вращения вала привода n_вых = 200 об/мин; передаточное число редуктора U_р = 2.25; угол наклона зуба β = 10 град.

Примечание: зубчатые колеса изготавливаются из стали 40XН, для которой допустимые контактные напряжения [σ_н]=450 МПа, твердость по методу Бринелля НВ=280.
Решение задачи:

1. Привод состоит из электродвигателя, ременной передачи и редуктора. Электродвигатель соединяется с входным валом редуктора с помощью ременной передачи, состоящей из ведущего 1 и ведомого 2 шкивов. Вращение от шкива 1 к шкиву 2 передается при помощи ремня. От шкива 2 вращение через зубчатую передачу (состоящую из шестерни 3 и зубчатого колеса 4) передается выходному валу.

2. Определение кинематических параметров привода

2.1 Подбор стандартного электродвигателя

Входная мощность Р_вх на валу электродвигателя, которая обеспечивает заданную мощность на выходном валу привода Р_вых, определяется с учетом потерь в элементах привода из формулы общего коэффициента полезного действия (КПД):

Общий КПД заданного привода η_общ определяем по формуле:
η_общ = η_рп · η_зп · η^k_подш
где η_рп – КПД ременной передачи, η_зп – КПД зубчатой передачи, η_подш – КПД одной пары подшипников. Для клиноременной передачи рекомендуется η = 0,95…0,96; для зубчатой цилиндрической передачи η = 0,97…0,98; КПД одной пары подшипников η = 0,99…0,995; k – число пар подшипников.

В соответствии с вышеизложенными рекомендациями, принимаем КПД

η_{рм =} 0,95, η_зп = 0,98, η_подш = 0,99. Анализируя конструкцию заданного привода (рис. 4), приходим к выводу, что в данной конструкции 2 пары подшипников (т.е. k = 2) Тогда:

η_общ = 0,95 · 0,98 · 0,992 = 0,912.

Входная (требуемая) мощность электродвигателя:
Рвх=1.1/0.912=1.2 кВт
По найденному значению Р_вх подбираем стандартный электродвигатель. При выборе электродвигателя должно быть выполнено условие Р_вх > Р_вх . С учетом этого условия принимаем электродвигатель 4А80B2У3 с номинальной мощностью Р_вх = 1.5 кВт и асинхронным числом оборотов вала электродвигателя η_вх = 1480 об/мин.

2.2 Определение передаточных чисел элементов привода

Передаточное число привода можно определить из соотношения:
Uпр=1480/200=7.4
Общее передаточное число привода представляет собой также произведение передаточного числа ременной передачи U_рем и цилиндрического редуктора U_р (т.е. U_пр = U_рем · U_р). Отсюда:

Uрем=7.4/2.25=3.3
Значение передаточного числа ременной передачи ориентировочно должно находится в пределах U_рем = 1,5…4, условие выполняется.

2.3 Определение частот вращения валов привода

Частоты вращения определяются с учетом рассчитанных передаточных чисел привода.

Частота вращения первого (ведущего) вала привода (вала электродвигателя) n₁ = n_вх = 1480 об/мин.

Частота вращения второго вала привода (входного вала редуктора):
n2=n1/uрем=1480/3.3=448 об/мин
Частота вращения третьего вала привода (выходного вала редуктора):
n3=n2/up=448/2.25=199 об/мин
2.4 Определение мощностей, передаваемых каждым валом привода

Мощности определяются с учетом значений КПД всех элементов привода. Мощность, передаваемая первым (ведущим) валом привода (валом электродвигателя) Р_І = Р_вх = 1.48 кВт.

Мощность, передаваемая вторым валом привода:
Р_ІІ = Р_І · ₁₂ · _подш = 1.48 · 0,95 · 0,99 = 1,39 кВт.
Мощность, передаваемая третьим валом привода:

Р_ІІІ = Р_ІІ · η₃₄ · _подш = 1,39 · 0,98 · 0,99 = 1,35 кВт.
2.5 Определение вращающихся моментов, передаваемых валами привода

Вращающие моменты, передаваемые каждым валом привода, определяются с учетом мощности Р (кВт) и частоты вращения вала n (об/мин) рассчитываемого вала по зависимости:

В соответствии с данной формулой, для первого вала привода:
Т1=9550х1.48/1480=9.55 Нхм

Для второго вала привода (входного вала редуктора):
Т2=9550х1.39/448=29.6Нхм
Для третьего вала привода (выходного вала редуктора):
Т3=9550х1.35/199=45.1Нхм

3. Определение межосевого расстояния редуктора

Для расчета межосевого расстояния используется формула: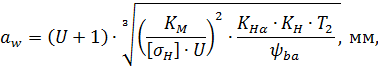

где U = U_р – передаточное число зубчатой передачи; Т₂ = Т_ІІІ – вращающий момент на ведомом на ведомом валу зубчатой передачи, Н·м; [] - допускаемое контактное напряжение для материала колеса, МПа; К_М – коэффициент, зависящий от вида передачи (для прямозубых колес К_М = 10000, для косозубых колес величина К_М = 8500); К_Н - коэффициент учета неравномерности распределения нагрузки по ширине зубчатого колеса (К_Н = 1,1...1,15); коэффициент ширины колеса = 0,25..0,4; К_На - коэффициент учета распределения нагрузки между зубьями (для прямозубых колес величина К_На = 1, для косозубых К_На = 1,05—1,1).

С учетом этих рекомендаций и полученных ранее значений, имеем Т₂ = Т_ІІІ = 45,1 Н·м (в соответствии с табл. 1); [] = 450 МПа (по условию);

U = U_p= 3,5 (по условию); К_М - 10000 (по условию зубчатые колеса прямозубые). Принимаем значения = 0,25, К_Н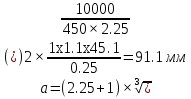а - 1, К_Н = 1,1.

Тогда:

Вычисленное межосевое расстояние следует округлить до стандартного ближайшего значения. При этом значения межосевого расстояния из первого ряда являются более предпочтительными.

На основании данного приложения и расчетов принимаем = 100 мм

4. Определение геометрических параметров зубчатой передачи

Основным параметром передачи является модуль зацепления m, величина которого выбирается из стандартного ряда. При этом значения модуля из первого ряда являются более предпочтительными.

Модуль зацепления назначают из интервала m = (0,01…0,02) · , мм.

С учетом данной зависимости получаем

m = 1…2 мм.

Принимаем стандартный модуль m = 1,25 мм .

Вычисляем суммарное число зубьев Z шестерни и колеса с учетом заданного угла наклона зубьев по формуле:

Принимаем Z = 160 (округляем до целого) и находим действительное значение угла: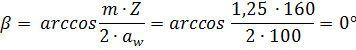

Число зубьев шестерни
Z3=160/2.25+1=49
Принимаем Z₃ = 49 (округляем до целого).

Число зубьев колеса Z₄ = Z - Z₃ = 160-49 = 111.

Фактическое передаточное число редуктора
Uф=111/49=2.26


Отличие U_p от U_ф:
2.26-2.25/2.26 х100=0.4%
(что меньше допустимого ± 5 %).

Определяем диаметры зубчатых колес.

Диаметры делительных окружностей:
Шестерни d3=1.25х49/0.984=62 мм
Колеса d4=1.25х111/0.984=141 мм
Фактическое межосевое расстояние

совпадает с = 100 мм.

Принимаем окончательно: m = 1,25 мм, Z₃ = 49, Z₄ = 111.

Диаметры вершин зубьев:
Dа3=62+2х1.25=64.5 мм

Da4=111+2х1.25=113.5 мм
Диаметры впадин зубьев:

шестерни Df3=62-2.5х1.25=58.875 мм

колеса Df4=111-2.5х1.25=107.875 мм
Рабочая ширина зубчатого венца b₄ определяется по принятому коэффициенту = 0,25. Из выражения = b₄/a_w находим:
b₄ = мм.
Принимаем ширину зубчатого венца b₄ = 25 мм.

Для того чтобы обеспечить передачу вращающего момента с шестерни на колесо, ширину шестерни назначают на 2..5 мм больше ширины колеса. Таким образом, примем ширину шестерни b₃ = 25 + 5 = 30 мм.

5. Определение сил, действующих в зубчатом зацеплении

В прямозубом зацеплении двух зубчатых колес (рис. 5) зубья шестерни воздействуют на зубья колеса равнодействующей силой F_n, которая раскладывается на окружную силу F_t и радиальную силу F_r (направленную от зуба к центру зубчатого колеса).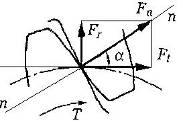


Рис. 5. Схема сил в зубчатом зацеплении.
Окружная сила определяется по зависимости:

где Т - вращающий момент на зубчатом колесе, Н мм; d- делительный диаметр зубчатого колеса, мм.

Радиальная сила определяется по зависимости:


где = 20° (угол зацепления).

С учетом вышеизложенного, приняв Т = Т_ІІІ = 45,1 ·10³ (вращающий момент на зубчатом колесе, Н ·мм) и d = d₄ = 124 (делительный диаметр зубчатого колеса, мм), величина окружной силы F_t будет равна:



Радиальная сила равна:

6. Выполнение предварительного расчета валов

Основным критерием работоспособности валов является условие их прочности: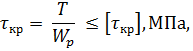

где - напряжение, возникающее при кручении вала, МПа; []- допускаемое напряжение при кручении, МПа; Т - вращающий момент, передаваемый валом, Н ·мм; W_p - полярный момент сопротивления круглого сечения, мм³.

Полярный момент сопротивления определяется по зависимости:

где d - диаметр вала, мм.

Поскольку в предварительных расчетах изгиб вала не учитывается, то расчет ведут по пониженным допускаемым напряжениям, которые выбирают из интервала [] = 25...30 МПа. Принимаем к расчету [] = 30 МПа.

Из приведенных зависимостей определяем диаметры выходных концов валов редуктора: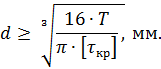

Для входного вала редуктора (момент Т = Т_ІІ = 13,37 · 10³ Н·мм):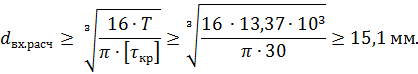

Для выходного вала редуктора (момент Т = Т_ІІІ = 45,1 · 10³ Н·мм):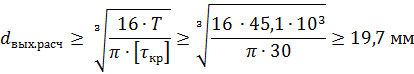

С учетом полученных значений примем диаметры выходных концов валов, руководствуясь нормальным рядом линейных размеров.

Принимаем диаметр входного конца вала редуктора 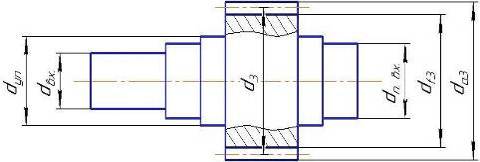16 мм (> ). Диаметры остальных частей вала (кроме диаметров шестерни d₃, d_a3 и d_f3) принимаются по конструктивным соображениям (рис. 6), при этом разница между диаметрами обычно составляет 3...5 мм (иногда больше).


Рис.6. Входной вал
Диаметр вала под подшипником d_п должен делиться на 5. Диаметр вала для упора d_уп должен быть больше d_п.

С учетом этого, принимаем диаметр входного вала под подшипником d_{п вх} = 20 мм, диаметр вала для упора d_уп = 24 мм.

Принимаем диаметр выходного конца вала редуктора d_вых = 20 мм

(d_вых > d_{вых расч}). Диаметры остальных частей вала принимаются по конструктивным соображениям (рис.7).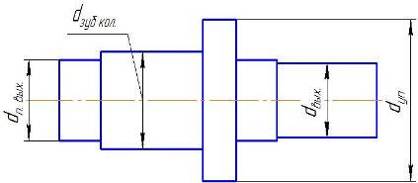


Рис. 7. Выходной вал
На основании вышеизложенных соображений, принимаем диаметр выходного вала под подшипником d_{п вых} = 25 мм, диаметр вала под зубчатым колесом d_{зуб кол} = 30 мм, диаметр вала для упора зубчатого колеса d_уп = 36 мм.

7. Подбор подшипников качения

Валы редуктора устанавливают в подшипники. Различают подшипники скольжения и качения. В редукторах чаще всего используются подшипники качения, которые состоят из наружного и внутреннего колец, тел качения и сепаратора (детали, служащей для удержания тел качения на определенном расстоянии друг от друга).

К основным геометрическим параметрам подшипника относятся: диаметры внутреннего d и наружного D колец, а также ширину подшипника В. Каждый подшипник имеет условное обозначение.

В редукторе, скомпонованном из прямозубых зубчатых передач, применяют радиальные шариковые подшипники. В редукторе, скомпонованном из косозубых зубчатых передач, применяют радиально-упорные шариковые подшипники.

В рассматриваемом примере редуктор скомпонован из прямозубых зубчатых передач. Поэтому для опор валов применяем радиальные шариковые подшипники.

С учетом определенного ранее диаметра входного вала под подшипником d_{п вх} = 20 мм принимаем подшипники 204 (для которых диаметр внутреннего кольца d = 20 мм, наружного кольца D = 47 мм, ширина В = 14 мм.

С учетом определенного ранее диаметра выходного вала под подшипником d_{п вых} = 25 мм принимаем подшипники 205 (для которых диаметр внутреннего кольца d = 35 мм, наружного кольца D = 52 мм, ширина В = 15 мм.

8. Разработка компоновочного эскиза редуктора

Компоновочный эскиз выполняется на базе имеющихся к настоящему моменту данных: межосевого расстояния a_w, диаметров шестерни и колеса (d₃, d_aз, d_f3, d₄, d_a4, d_f4), ширины шестерни b₃ и зубчатого колеса b₄, диаметров всех частей входного и выходного валов, а также размеров подшипников. Целью компоновочного эскиза является проработка конструкции и размещения деталей редуктора.

Компоновочный эскиз выполняем на одном листе формата А3.

Компоновочный эскиз выполняется в масштабе 1:1. Построение начинается с осевых линий валов, отстоящих друг oт друга на расстоянии a_w. Затем прочерчиваются контуры шестерни и колес по известным диаметрам и ширине.

Далее прочерчивается внутренний контур корпуса редуктора. При этом расстояние = 8... 12 мм обеспечивает зазор между торцами колес и внутренним контуром корпуса редуктора.

Далее прочерчиваются контуры подшипников. При этом для входного вала принимают размеры d_{п вх} = 20 мм D_{п вх} = 47 мм, = D, В = 14 мм. Для выходного вала принимают размеры d_{п вых} = 25 мм D_{п вых} = 52 мм, В = 15 мм.

После подшипников прочерчивается наружный контур корпуса редуктора. При этом принимается расстояние ₁ = 5...10 мм.

Завершающим этапом является вычерчивание длин концов валов (длина (1,5...1,6)·d, где d - диаметр выходного конца вала, мм). С учетом этого, принимаем длину выходного конца входного вала (принимаем длину = 24 мм), выходного конца выходного вала (принимаем длину = 30 мм)

кривошипный ускорение тормозной привод
Список литературы
1.Джамая В.В. Прикладная механика: учебник для студентов высших учебных заведений. - М.: Дрофа, 2004.

2. Скойбеда А.Т. Прикладная механика: учебник для студентов высших учебных заведений. - Минск: Выш. шк., 1997.

3. Иванов М.Н., Финогенов В.А. Детали машин: учебник для вузов. 8-е издание. - М.: Выс. шк., 2004.

4. Дунаев П.Ф., Леликов О.П. Конструирование и деталей машин: учебное пособие для технических специальностей вузов. 8-е издание. - М.: Издательский центр «Академия», 2004.

5. Саргсян А.Е. Сопротивление материалов, теории упругости и пластичности. - М.: Выс. шк., 2000.