дифур2 (копия). Закон изменения со временем (t) численности бактерий (n), помещенных в питательную среду
 Скачать 294.64 Kb.
|
|
1  2  3  4. Рассмотрим микробиологическую задачу. Установим закон изменения со временем (t) численности бактерий (n), помещенных в питательную среду. Для составления дифференциального уравнения, отражающего существование бактерий в этих условиях, необходим некоторый факт, который следует записать в математической форме. На основании экспериментальных данных и общих соображений таким фактом может служить утверждение: “скорость размножения бактерий (математически dn/dt ) пропорциональна их числу (n) в данный момент времени”. Таким образом, необходимое дифференциальное уравнение имеет вид: dn/dt кn, (1) где к - доступный экспериментальному определения коэффициент пропорциональности, зависящий от вида бактерий и параметров среды их обитания. Дополнительные данные, необходимые для решения задачи следуют из начального условия: при t = 0, n = n0 , т.е. в начальный момент времени количество бактерий считается известным и равным n0 . Для решения уравнения (1) произведем разделение переменных и последующее интегрирование: dn/n kdt ln|n| = kt + ln|C| . (2) Произвольную постоянную в уравнении (11) удобно представить в виде lnС . Из начального условия: C = n0. Решая логарифмическое уравнение (2) с учетом начального условия, получим искомый закон изменения числа бактерий со временем: n=n0 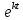 . (3)Произведем некоторый анализ результата. В чем его сиюминутная практическая полезность и возможные более отдаленные выводы? 1) Зная коэффициент к и начальное число бактерий n0 , легко определить их число в любой момент времени t. 2) Прирост бактериальной массы определяется через коэффициент к условиями среды обитания бактерий. Чем больше значение к, тем быстрее увеличивается число бактерий 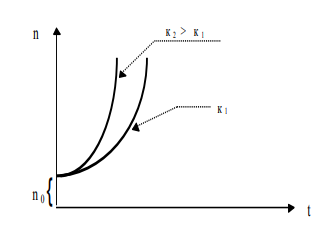 Если существуют факторы, препятствующие размножению бактерий (повышенная температура, ионизирующие излучения и др.), то коэффициент к в формулах (1) - (3) уменьшается и может принять отрицательное значение - в этом случае будет наблюдаться гибель бактерий. 3) С некоторым риском можно попытаться придать полученному для бактерий результату (3) большую общность и сформулировать утверждение: «любой биологический вид, находясь в оптимальных для своего существования условиях, экспоненциально увеличивает свою численность со временем». Примеры справедливости этого утверждения можно наблюдать. Так, кролики, завезенные в Австралию, где практически нет хищников, которые бы ими питались, увеличили свое число в соответствии с формулой (3) и стали представлять серьезную опасность для сельского хозяйства. 5. Определить во сколько раз увеличится количество бактерий за 9 часов, если в течение 3 часов их количество изменилось от 100 до 200. Решение. Как уже было сказано выше, скорость размножения бактерий, если для них имеется достаточный запас пищи и созданы другие необходимые внешние условия (например, отсутствие подавления бактерий другими видами), пропорциональна их количеству. Пусть х – количество бактерий в данный момент, тогда скорость изменения их количества равна производной 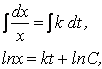 . Так как скорость размножения бактерий пропорциональна их количеству, то существует k, что  Разделяем в дифференциальном уравнении переменные:  Интегрируя, получаем: что после потенцирования даёт  Для нахождения С используем начальное условие: при t=0, х=100. Имеем: Се=100, С=100, и, значит, х=100  . Коэффициент  находим из условия: приt=3, х=200:   Искомая функция:  . При t=9, х=800.Ответ: количество бактерий за 9 часов увеличится в 8 раз. Первая фаза (латентная) определяется факторами адаптации к питательной среде. В это время микроорганизмы только осваиваются с новыми условиями. Рост бактерий не наблюдается. Вторая фаза (экспоненциальная) характеризуется ростом в геометрической прогрессии (увеличение по экспоненциальной кривой). В этот период бактериальные клетки активно растут, используя всю доступную пищу (максимальная скорость роста). Достигнув определенного размера, бактерия начинает делиться, причем процесс размножения протекает с постоянной скоростью, так как запасов пищи пока достаточно. В результате увеличившейся скорости роста и размножения происходит накопление в среде отходов жизнедеятельности (токсинов). К концу фазы скорость роста начинает уменьшаться. Третья фаза характеризуется стационарным ростом, т. е. количество «новорожденных» клеток совпадает с числом отмерших. Кривая роста и размножения на этом отрезке больше не поднимается. Скорость роста замедляется. Какое-то время общая численность бактерий в питательной среде остается неизменной. Однако за счет появления новых «членов семьи» запасы питательных веществ уменьшаются, а токсичность среды увеличивается. Этот процесс ухудшает условия жизни всей колонии. Источник: https://probakterii.ru/prokaryotes/vital-functions/rost-i-razmnozhenie-bakterij.html |