Ответы на вопросы по подземной гидромеханике УГНТУ. Подземная гидромеханика
 Скачать 1.82 Mb. Скачать 1.82 Mb.
|
|
Подземная гидромеханика Под пористой средой понимается множество твердых частиц, тесно прилегающих друг к другу, сцементированных или несцементированных, пространство между которыми (поры, трещины) может быть заполнено жидкостью или газом. Горные породы, обладающие способностью вмещать нефть, газ и воду и отдавать их под действием перепада давлений, называются породами-коллекторами. В большинстве случаев коллекторами являются песчаники (алевролиты, песчаники) и карбонатные (известняки, доломиты) породы. Коллекторские свойства горных пород обусловлены наличием в них пустот – пор, каверн и трещин, которые заполнены нефтью, газом или водой. Поры – пространства между отдельными зернами, слагающими породу. Классификация коллекторов: По типу пустотного пространства: А) поровые - коллекторы, представленные песчано-алевритовыми породами, реже известняками и доломитами (оолитовыми и органогенными); поровое пространство в них состоит из межзерновых, межоолитовых и биопустотных полостей. Б) Трещинные коллекторы сложены преимущественно карбонатами, реже терригенными породами; поровое пространство в них образуется системой трещин. При этом участки коллектора между трещинами представлены плотными непроницаемыми и малопроницаемыми нетрещиноватыми блоками пород, поровое пространство в которых практически не участвует в процессах фильтрации. В) Каверновые коллекторы сложены в основном карбонатными породами; пустотное пространство в них представлено кавернами выщелачивания Г) В коллекторах смешанного типа отмечается сочетание систем трещин, порового пространства блоков и пор. Классификация коллекторов по типу горных пород: Терригенные Карбонатные Поры могут быть сообщающимися и несообщающимися. Сообщающиеся образуют эффективное поровое пространство. Совокупность сообщающихся и несообщающихся пор образуют общее поровое пространство. Пористые материалы по структуре разделяют на неупорядоченные и упорядоченные: К неупорядоченным пористым средам относятся естественные горные породы. К упорядоченным пористым средам относят два вида грунта: фиктивный и идеальный. Фиктивный грунт – грунт или система, составленный из шариков одинакового диаметра при правильной их упаковке. Идеальный грунт – система цилиндрических поровых каналов одинакового диаметра и параллельны друг к другу. Основные емкостные и динамические характеристики пористых сред Пористость горных пород – наличие в горной породе пустот и пор. Пористость показывает какой объем запасов нефти и газа может содержаться в пустотах. Для оценки пористости горных пород введены три коэффициента: Коэффициент общей пористости – отношение объема всех пустот в породе к объему образца: 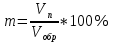 . Измеряется в процентах или долях. . Измеряется в процентах или долях.Коэффициент открытой пористости – отношение суммарного объема открытых взаимосвязанных пор к общему объему образца породы: 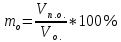 . Измеряется в процентах или долях. . Измеряется в процентах или долях.Коэффициент динамической пористости – отношение суммарного объема пор, в котором жидкость или газ при существующем перепаде давления (градиенте давления) охвачены фильтрацией, к общему объему образца породы: 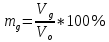 . Измеряется в процентах или долях. . Измеряется в процентах или долях.Пористость коллекторов изменяется от долей % до 52%. Просветность или поверхностная пористость пород — это часть сечения пород, которая свободна для прохода газа или жидкости. Она характеризуется коэффициентом просветности (n), который представляет отношение площади поперечного сечения пор (Sn) к площади породы (S), т. е. 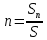 . Важное значение представляет определение не наименьшего, а среднего значения просветности (nс) для данного объема пород. . Важное значение представляет определение не наименьшего, а среднего значения просветности (nс) для данного объема пород. Проницаемость – способность горных пород пропускать через себя жидкости и газы при наличии перепада давления. Коэффициент проницаемости показывает суммарную площадь пор, сквозь которую проходит фильтрация жидкостей и газов. 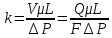 . . Различают следующие коэффициенты проницаемости: Абсолютная проницаемость – проницаемость горных пород, которая определяется при фильтрации в ней лишь одной фазы, инертной не взаимодействующей с пористой средой. Зависит только от свойств самой породы. Эффективная (фазовая) проницаемость – проницаемость г.п. для одной из движущихся в порах двухфазной или многофазной системы. Коэффициенты фазовых проницаемостей определяются из закона фильтрайии Дарси: 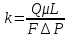 Относительная проницаемость – отношение фазовой проницаемости к абсолютной проницаемости. Измеряется проницаемость в мм2, мкм2, D. Проницаемость пород меняется в пределах 0,001 – 5 мкм2. Теория фильтрации Движение жидкостей, газов и их смесей через твердые (деформируемые) тела, содержащие связанные между собой поры или трещины, называется фильтрацией. Теория фильтрации, являющаяся разделом механики сплошной среды, получила большое развитие в связи с потребностями гидротехники, гидромелиорации, гидрогеологии, горного дела, нефтегазодобычи, химической технологии и т.д. Теоретической основой разработки нефтегазоводоносных пластов служит нефтегазовая подземная гидромеханика, изучающая фильтрацию нефти, газа и воды в пористых и (или) трещиноватых горных породах. Чтобы от фиктивного грунта перейти к естественному грунту используют понятие эффективный диаметр. Обозначается dф. Эффективный диаметр частиц естественного грунта – диаметр частиц такого фиктивного грунта, который имеет такое же сопротивление, как и естественный грунт. Скорость движения жидкостей и газов в пористых средах – величины очень и очень малые. Скорость фильтрации и её связь со скоростью движения При изучении микродвижения жидкостей и газов в пласте используют понятие средне истинная скорость движения жидкости. Она обозначается w. Площадь фильтрации – суммарная площадь пустот и зерен, находящихся в просматриваемом поперечном сечении. Для изучения законов распределения давления и закона распределения других параметров используется понятие скорость фильтрации (v). Скорость фильтрации – такая воображаемая скорость, с которой двигалась бы жидкость между кровлей и подошвой пласта, если бы самой пористой среды не было. 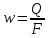 , где F – площадь фильтрации. , где F – площадь фильтрации.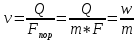 Абсолютная скорость движения жидкости – скорость, когда вся масса жидкости находится в движении. Динамическая скорость движения жидкости – скорость той жидкости, которая находится в движении. Капиллярная скорость – средняя скорость движения жидкости в той части порового канала, где жидкость неподвижна, но теоретически ее движение возможно. Линейный закон фильтрации Дарси В 1856 году Дарси проводил исследование для улучшения системы водоснабжения и изучал приток воды к колодцам через песчаные фильтры. И установил основной закон. Линейный закон фильтрации Дарси – основное соотношение теории фильтрации. Он устанавливает связь между вектором скорости фильтрации и тем полем давления, которое вызывает фильтрационное течение. Дарси получил экспериментальную формулу 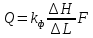 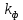 – коэф. фильтрации, определяется экспериментально в приборе пермеаметре, который содержит образец исследуемого грунта. – коэф. фильтрации, определяется экспериментально в приборе пермеаметре, который содержит образец исследуемого грунта. Q – общий расход фильтрационного поток, поддерживается постоянно; H1, H2 – напоры, которые измеряются двумя пьезометрами (в сечениях 1 и 2 установлены пьезометры для определения напоров); z1, z2 – геометрические отметки (превышение центров сечений над плоскостью сравнения), p1, p2 – давления; расстояние между сечениями - ∆L. Q = const, следовательно речь идет об установившейся или стационарной фильтрации. 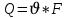 С 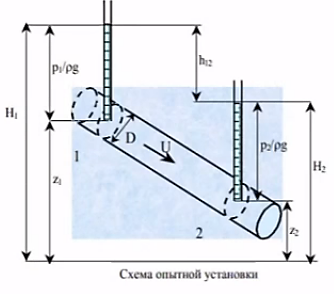 опоставив формулы, получаем: опоставив формулы, получаем: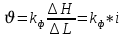 , i – градиент напора или гидравлический уклон. , i – градиент напора или гидравлический уклон. 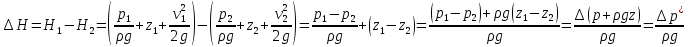 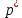 - приведенное давление, - приведенное давление, 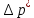 - изменение приведенного давления. - изменение приведенного давления.Коэффициент фильтрации 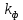 имеет размерность скорости, зависит от структуры пористой среды и от свойств фильтрующихся жидкостей. Коэффициент фильтрации характеризует расход потока через единицу площади сечения перпендикулярного к потоку под действием единичного градиента напора. имеет размерность скорости, зависит от структуры пористой среды и от свойств фильтрующихся жидкостей. Коэффициент фильтрации характеризует расход потока через единицу площади сечения перпендикулярного к потоку под действием единичного градиента напора.Подставим 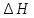 : : 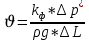 В дифференциальной форме получим формулу: 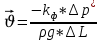 Знак показывает, в какую сторону направлен вектор скорости фильтрации. Вектор скорости фильтрации направлен в сторону убывания приведенного давления. При изучении фильтрационного потока давление всегда надо приводить к одному уровню. Особенно это необходимо в случае фильтрации в пласте наклонного вида или если пласт имеет большую толщину. Необязательно приводить давление, если пласт горизонтальный z=0, следовательно, p*=p, или в случае фильтрации газа. Закон Дарси справедлив для следующих условий: Пористая среда – мелкозернистая; Скорость фильтрации и градиенты давления – величины малые; Скорость фильтрации и градиенты давления изменяются очень медленно во времени и практически постоянны; Жидкость должна быть ньютоновская. В 1930 году ученый Нутинг предложил ввести параметр, который назвал коэф. проницаемости. Введя такое обозначение, сформулируем линейный фильтрации Дарси: Скорость фильтрации прямо пропорциональна градиенту давления и обратно пропорциональна динамической вязкости. 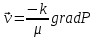 Границы применимости закона Дарси В процессе всех исследований по проверке закона Дарси показано, что можно выделить верхнюю и нижнюю границу применимости. Нижняя граница определяется проявлением неньютоновсих реологических свойств жидкости, ее взаимодействием с твердым скелетом пористой среды при достаточно малых скоростях фильтрации. Верхняя граница наиболее полно изучена. Здесь отклонения, вызванные проявлением инерционных сил при увеличении скорости фильтрации. Число Рейнольдса Re: 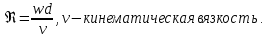 Попытки не увенчались успехом, у всех получилось свое критическое значение числа Рейнольдса. Нелинейные законы фильтрации Одночленная форма записи: 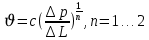 При n=2 получаем формула Краснопольского: 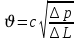 Двучленная форма записи: 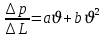 где, a и b – параметры, которые определяются экспериментально или по формулам справочных материалов. При малых скоростях: 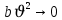 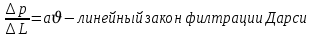 Вторя форма записи более физически обоснованная, потому что скорости фильтрации величины малые. 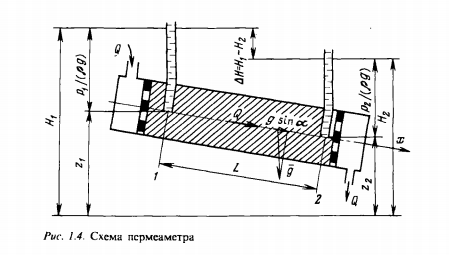 Обобщенный закон Дарси Обобщение через потенциальную функцию Обобщение при многофазном течении флюидов О 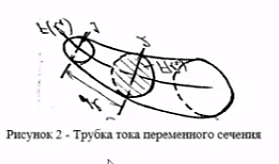 бобщение через потенциальную функцию: бобщение через потенциальную функцию:Трубка тока – элемент порового канала, по которому идет фильтрация. Пусть во всех сечениях нормальных к оси трубки тока площади сечения F меняются по длине. Нормальные к оси трубки тока сечения являются изобарические, т.е. давления равны. Из условия неразрывности фильтрационного потока следует, что массовый расход жидкости или газа через все изобарические сечения будет один и тот же. 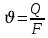 Чтобы перейти к массовым параметрам, нужно умножить левую и правую часть на плотность: 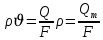 , Qm – массовый расход жидкости или газа. , Qm – массовый расход жидкости или газа.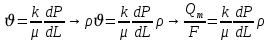 В общем случае k, μ, ρ зависят от давления, поэтому можно разделить переменные. Введем понятия потенциальной функции (потенциал функции): 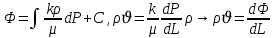 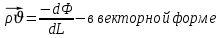 Введение потенциальной функции позволяет обобщить линейный закон фильтрации Дарси для случая фильтрации жидкости, газа, газированной жидкости, рассматривать их движение в упругих пластах и учитывать зависимости плотности, проницаемости, вязкости от давления. Обобщенный закон гласит: массовая скорость фильтрации прямо пропорциональна градиенту потенциальной функции или градиенту потенциала скорости. Движение флюида при справедливости потенциальной функции называют потенциальным движением. Потенциальное движение газа или жидкости – движение, при котором массовая скорость фильтрации прямо пропорциональна градиенту потенциальной функции. Обобщение при многофазном течении флюидов Здесь играет роль: Скорость фильтрации i-ой фазы 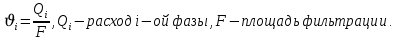 Насыщенность порового пространства i-ой фазой. 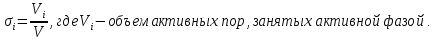 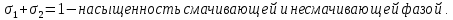 Экспериментально установлено, что для каждой фазы объемный расход Q возрастает с увеличением перепада давления и насыщенности данной фазой. 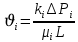 Относительная фазовая проницаемость 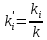 Введенные понятия можно обобщить на случай течения 3-х несмешивающихся флюидов. Дифференциальные уравнения фильтрации жидкостей и газа в пористой среде Задачи неустановившейся фильтрации жидкостей и газа в пористой среде решаются методами математической физики. Для этого составляются и решаются ДифУры. Обычно диф.уры. составляют по отношению к бесконечно малому элементу пористой среды и рассматривают изменение происходящие в этом элементе за бесконечно малый интервал времени. В большинстве случаев эти дифуры составляются в частных производных. Решение их не всегда возможно, но и в этом случае они представляют интерес, так как из них можно получить безразмерные критерии подобия и найти сходства с другими изученными явлениями. В подземной гидромеханике максимальное число неизвестных функций – 8. P=P(x, y, z, t) – закон распределения давления в пласте Закон распределения скорости фильтрации: Vx= Vx(x, y, z, t) на ось OX Vy= Vy(x, y, z, t) на ось OY Vz= Vz(x, y, z, t) на ось OZ Свойства добываемых флюидов: Динамическая вязкость µ= µ(x, y, z, t) Плотность ρ=ρ(x, y, z, t) Свойства пористой среды: Коэф. пористости m=m(x, y, z, t) Коэф. проницаемость k=k(x, y, z, t) Частные случаи: Несжимаемая жидкость: µ=const, ρ=const. Недеформируемая пористая среды: k=const, m=const. Изотермические процессы: Фильтрация – очень медленный процесс, поэтому температурные изменения успевают компенсироваться с окружающей средой, т.е. окружающими г.п. Аналитически решить систему уравнений очень сложно, поэтому приходится прибегать к использованию численных методов с помощью программных комплексов. В систему уравнений для определения переменных параметров фильтрационного потока входят следующие уравнения: Уравнение неразрывности или сплошности фильтрационного потока; Уравнения движения (в 3-х проекциях); Уравнения состояния пористой среды и флюидов. Для решения этой системы уравнений задаются граничные условия (ГУ) на границе пласта и начальные условия (НУ) на начальный момент времени. Совокупность перечисленных ДУ, а также ГУ и НУ (краевые условия) составляет задачу математической физики или краевую задачу подземной гидромеханики. |
