Ответы на вопросы по подземной гидромеханике УГНТУ. Подземная гидромеханика
 Скачать 1.82 Mb. Скачать 1.82 Mb.
|
|
Уравнение неразрывности или сплошности фильтрационного потока Выведем это уравнение для общего случая (для однородного сжимаемого флюида в деформируемой пористой среде): Уравнение неразрывности выражает баланс массы сжимаемой жидкости в пределах постоянного элементарного объема, выделенного внутри пористой среды: Внутри выделенного объема нет ни стоков, ни источников. Источник – предельное положение нагнетательной скважины, радиус которой стремится к нулю. Сток – предельное положение добывающей скважины, радиус которой стремится к нулю. 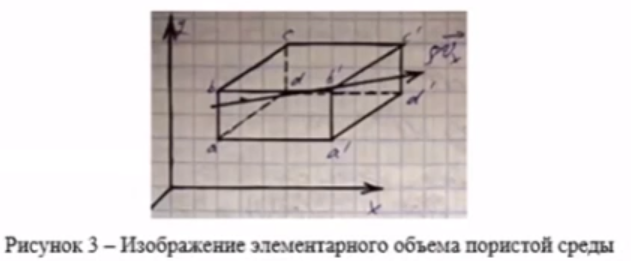 Объем параллелепипеда равен: 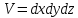 Рассмотрим движение вдоль оси OX: Через грань ABCD втекают (за бесконечно малый интервал времени dt) следующая масса флюида 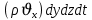 . Через грань A’B’C’D’ вдоль оси OX вытекает за время dt следующая масса жидкости: . Через грань A’B’C’D’ вдоль оси OX вытекает за время dt следующая масса жидкости: 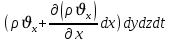 Изменение массы флюида за время dt за счет потока вдоль оси OX равно: 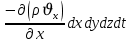 Рассуждая следующим аналогичным образом, рассматривая движения вдоль осей OY, OZ, можно записать такие же изменения вдоль других координатных осей: 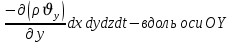 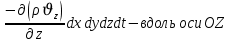 Учитывая выше сказанное, запишем общее изменение массы: 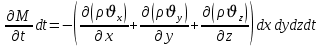 С другой стороны, масса флюида находится в поровом объеме dxdydzm. Масса флюида, которая находится в поровом пространстве: 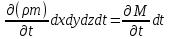 m, ρ – величины переменные  Поэтому общее изменение массы можно записать как: Поэтому общее изменение массы можно записать как: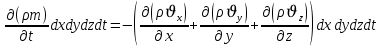 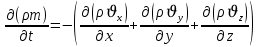 Получено уравнение неразрывности для общего случая – для неустановившейся фильтрации сжимаемой жидкости в деформируемом пласте. 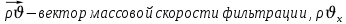 , , 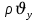 , , 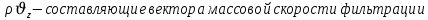 . .Представим через дивергенцию векторного поля массовой скорости фильтрации (оператор Гамильтона): 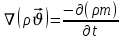 Уравнение неразрывности в укороченном виде. Если фильтруются несжимаемая жидкость в недеформируемой пористой среде, то уравнение можно записать только через скорость: 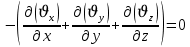 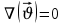 Для установившегося фильтрационного потока: 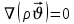 Для всех установившихся фильтрационных течений все уравнения будут приравниваться к нулю и носят название уравнение Лапласа. Дифференциальные уравнения движения флюидов в пористой среде Линейный закон фильтрации Дарси: 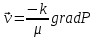 Последовав идее разложения фильтрационного потока на 3 составляющих вдоль координатных осей: 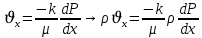 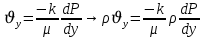 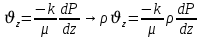  Введем потенциальную функцию течения или потенциал скорости: Введем потенциальную функцию течения или потенциал скорости: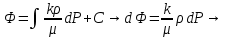 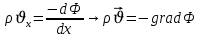 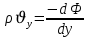 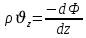 Используя введение потенциальной функции, запишем уравнение неразрывности и выразим его через потенциальную функцию: 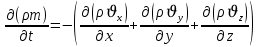 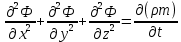 Уравнение неразрывности через потенциальную функцию. Для установившейся фильтрации: 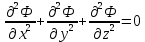 Уравнения состояния жидкостей, газов и пористой среды Для жидкостей: Плотность: По закону Гука: 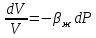 Так как V=M/ρ, тогда: 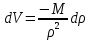 Подставим выражение для V и dV в первое выражение: 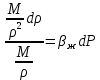 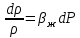 Интегрируя, получим: 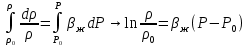 При больших значениях P: 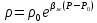 При малых значениях P: 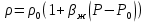 βн – (7 – 30)*10-10 Па-1 βв – (2,5 – 5)*10-10 Па-1 Вязкость Эксперименты показывают, что коэффициенты вязкости нефти (при давлениях выше давления насыщения) и газа увеличиваются с повышением давления. При изменении давления в значительных пределах (до 100 МПа) зависимость вязкости пластовых нефтей и природных газов от давления можно принять экспоненциальной: При больших значениях P: 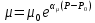 При малых значениях P: 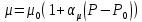 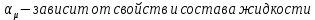 . . На вязкость большое значение имеет температура жидкости. Для газов: 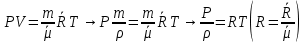 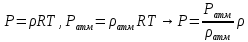 Для реальных газов: 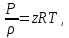 где z – коэффициент, характеризующий степень отклонения состояния реального газа от закона идеальных газов (коэффициент сверхсжимаемости) и зависящий от давления и температуры z = z(P, T), Значения коэффициента сверхсжимаемости z определяются по графикам Д. Брауна в зависимости от приведенных величин абсолютного давления и температуры. где z – коэффициент, характеризующий степень отклонения состояния реального газа от закона идеальных газов (коэффициент сверхсжимаемости) и зависящий от давления и температуры z = z(P, T), Значения коэффициента сверхсжимаемости z определяются по графикам Д. Брауна в зависимости от приведенных величин абсолютного давления и температуры.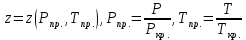 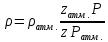 Причем 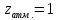 к-т сжимаемости. к-т сжимаемости.При больших значениях P: 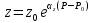 При малых значениях P: 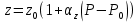 αz – коэффициент, зависящий от состава газа и определяемый опытным путем. Для пористой среды: Пористость: При больших значениях P: По закону Гука: 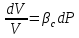 Изменение объема: 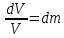 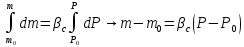 Для небольших перепадов давления: 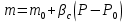 Для больших перепадов давления: 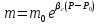 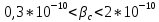 Проницаемость: При больших перепадах давлений: 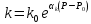 При малых перепадах давлений: 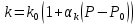 где 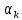 – зависит от состава и свойств породы. – зависит от состава и свойств породы.Краевые задачи подземной гидромеханики Краевые задачи подземной гидромеханики подразделяются на прямые и обратные Исходные данные для прямой задачи ПГ: Исходное ДУ Геометрические размеры пласта Коллекторские свойства пласта Свойства флюидов Граничные условия (для установившейся фильтрации) и начальные условия (для неустановившейся фильтрации) Требуется определить: Закон распределения давления Градиент давления Скорость фильтрации Дебит Закон движения Средневзвешенное давление по пласту и др. Исходные данные для обратной задачи ПГ: Аналитические выражения распределения давления в пласте Дебит или расход Законы движения Заданные экспериментальные зависимости этих параметров по результатам исследований Требуется определить: Фильтрационные параметры пласта: 1) Гидропроводность пласта 2) Подвижность жидкости в пласте 3) Проводимость пласта 4) Пьезопроводность пласта 5) Коэффициент продуктивности Геометрические размеры пласта Режим работы пласта и другие параметры Допущения и упрощения, принятые при моделировании прямых задач: Упрощение по форме залежи По геологическому строению Упрощение контура питания (КП) скважин. При этом радиус КП составит Rk=2σ *1/2=σ Сток и источник в качестве отображения нагнетательной и добывающей скважин соответственно. Источник – предельное положение нагнетательной скважины, радиус которой стремится к нулю. Сток – предельное положение добывающей скважины, радиус которой стремится к нулю. Галерея скважин. Галерея скважин – сплошная прямолинейная горная выработка, скрывшая продуктивный пласт на всю его толщину. Дифференциальное уравнение установившейся фильтрации несжимаемой жидкости по закону Дарси На основании уравнения неразрывности и упругого состояния пористой среды запишем: 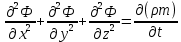 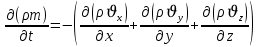 Для установившейся фильтрации: 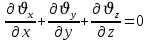 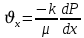 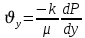 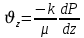 Получаем ДУ установившейся фильтрации несжимаемой жидкости по закону Дарси в недеформируемой пористой среде: 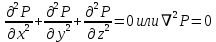 Если ввести понятие потенциальной функции: 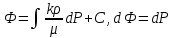 То получаем уравнение Лапласа через потенциальную функцию: 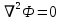 Функции, удовлетворяющие уравнениям Лапласа, являющиеся непрерывными функциями, имеющие непрерывные частные производные I и II порядка, называются гармоническими. Простейшие фильтрационные потоки Существуют три типа одномерных фильтрационных потоков: Прямолинейно-параллельный поток Плоскорадиальный поток Радиально-сферический поток П 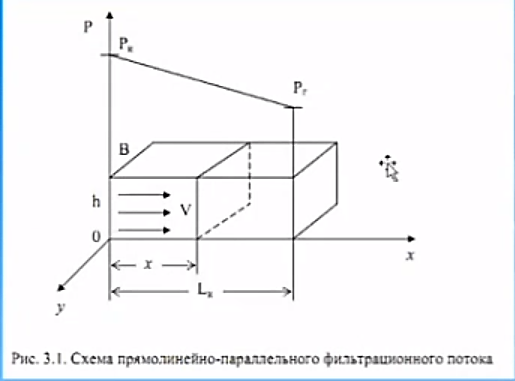 рямолинейно-параллельный поток имеет место в тех случаях, когда траектории всех частиц флюида являются прямыми линиями, а скорости фильтрации во всех точках любого поперечного сечения потока равны друг другу. При решении задач данный поток будет моделироваться галереями скважин. При изучении движения картина скоростей, давлений – это все прямые линии, причем скорости фильтрации во всех точках любого поперечного сечения равны. рямолинейно-параллельный поток имеет место в тех случаях, когда траектории всех частиц флюида являются прямыми линиями, а скорости фильтрации во всех точках любого поперечного сечения потока равны друг другу. При решении задач данный поток будет моделироваться галереями скважин. При изучении движения картина скоростей, давлений – это все прямые линии, причем скорости фильтрации во всех точках любого поперечного сечения равны. Плоскорадиальный поток имеет место в случае (если скважина добывающая), когда все частицы жидкости или газа движутся в одной плоскости по горизонтальным прямолинейным тракеториям, радиально сходящимся к одной точке или к центру скважины прямые линии. Для нагнетательной скважины радиально расходящиеся от центра скважины прямые линии. Гидродинамически совершенная скважина. Плоскорадиальный поток имеет место в случае (если скважина добывающая), когда все частицы жидкости или газа движутся в одной плоскости по горизонтальным прямолинейным тракеториям, радиально сходящимся к одной точке или к центру скважины прямые линии. Для нагнетательной скважины радиально расходящиеся от центра скважины прямые линии. Гидродинамически совершенная скважина.Р 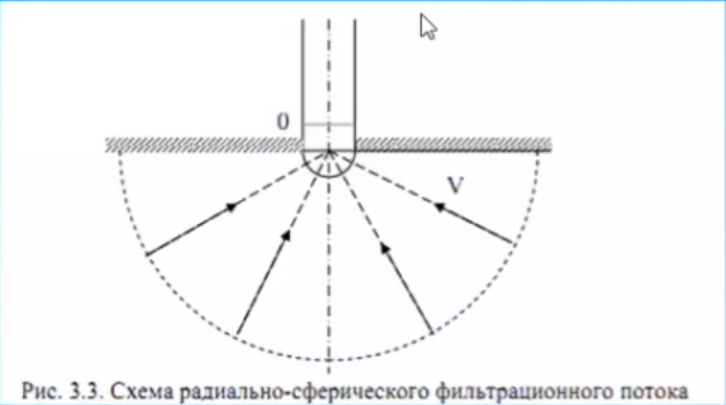 адиально-сферический поток (встречается достаточно редко) имеет место в случае, когда скважина вскрывает только кровлю пласта или глубина вскрытия значительно меньше толщины залежи (пласта). При этом траектории движения всех частиц жидкости или газа в пласте будут прямолинейными и радиально сходящимися в центре полусферического забоя. адиально-сферический поток (встречается достаточно редко) имеет место в случае, когда скважина вскрывает только кровлю пласта или глубина вскрытия значительно меньше толщины залежи (пласта). При этом траектории движения всех частиц жидкости или газа в пласте будут прямолинейными и радиально сходящимися в центре полусферического забоя. Все эти типы потоков относятся к одномерным, поскольку давление и скорость фильтрации являются функциями только одной координаты (линейной или радиуса). Дифференциальные уравнения потока  Прямолинейно-параллельный ФП. ДУ установившейся фильтрации однородной жидкости по закону Дарси: 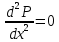 ДУ через потенциальную функцию: 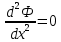 Плоскорадиальный ФП (поток с осевой симметрией):  Выведем уравнения: Выведем уравнения: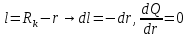 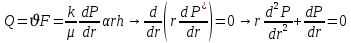 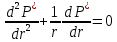 – 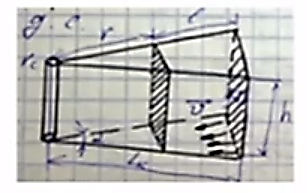 уравнение Лапласа в полярных координатах для установившегося плоскорадиального фильтрационного потока несжимаемой жидкости по закону Дарси. уравнение Лапласа в полярных координатах для установившегося плоскорадиального фильтрационного потока несжимаемой жидкости по закону Дарси. Радиально-сферический ФП (движение с центральной симметрией)  Выведем уравнение: Выведем уравнение: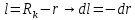 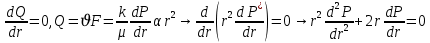 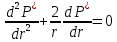 – 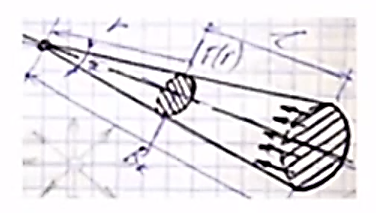 уравнение Лапласа в сферических координатах для установившегося радиально-сферического фильтрационного потока несжимаемой жидкости по закону Дарси. уравнение Лапласа в сферических координатах для установившегося радиально-сферического фильтрационного потока несжимаемой жидкости по закону Дарси.Порядок решения прямой краевой задачи Выписывается соответствующее этому случаю ДУ движения нефти и газа в пласте Интегрирование этого уравнения; получаем общее решение Задаемся ГУ и НУ Подставляем ГУ и НУ в общее решение, находим частное интегрирование Подставляем их в общее решение, получаем частное решение – закон распределения давления Берем первую производную – градиент давления Из линейного закона Дарси находим скорость фильтрации υ Используя площади фильтрации, определяем дебит или расход Q Находим закон движения t, далее средневзвешенное пластовое давление 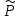 и т.д. и т.д.Установившаяся прямолинейная фильтрация несжимаемой жидкости в однородном пласте по линейному закону Дарси (приток галереи)  Pг 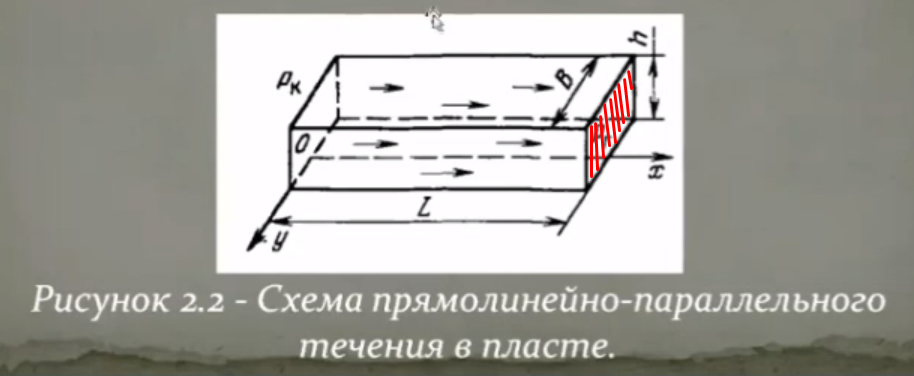
Решение: Запишем ДУ 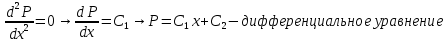 Граничные условия: P= Pk, x=0 => Pk=C2 P= PГ, x=Lk => PГ=C1* Lk+C2= C1* Lk+ Pk 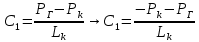 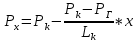 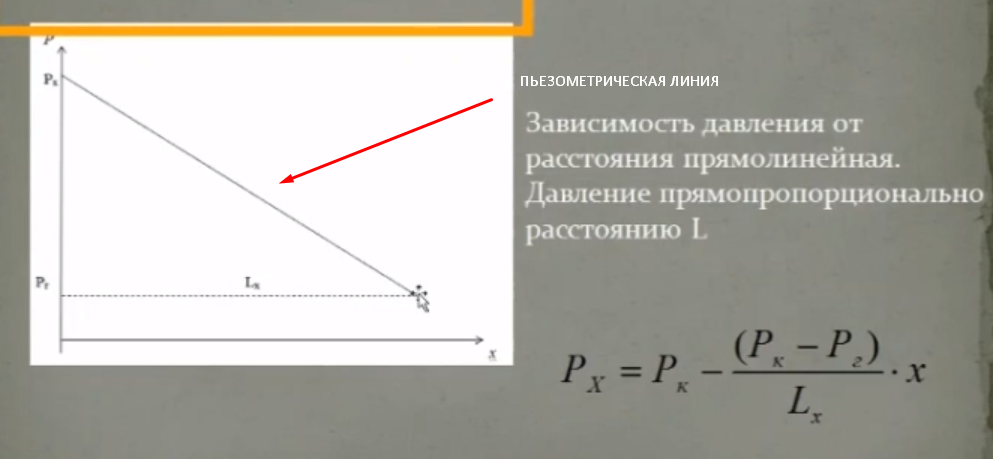 Закон распределения давления в полосообразном пласте. Закон распределения давления в полосообразном пласте.Линейный закон распределения давления по однородному пласту Найдем градиент давления: 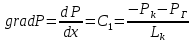 Определим скорость фильтрации: 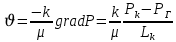  Определим приток галереи 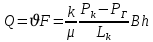 Время движения жидкости от контура питания до галереи: 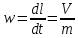 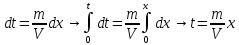 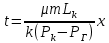 Средневзвешанное давление по пласту: 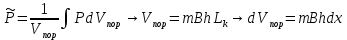 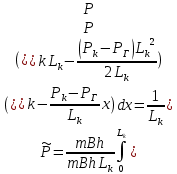 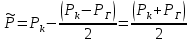 Средневзвешанное давление по пласту  Вывод: для установившегося прямолинейно параллельного потока несжимаемой жидкости в однородном пласте P=P(x) носит линейный характер (пьезометрическая линия); Q не зависит от координаты x (Q=const); υ не зависит от координаты x (υ=const); gradP не зависит от координаты x (gradP=const); гидродинамическое поле представлено двумя семействами взаимно перпендикулярных прямых линий: изобар и линий тока Вывод: для установившегося прямолинейно параллельного потока несжимаемой жидкости в однородном пласте P=P(x) носит линейный характер (пьезометрическая линия); Q не зависит от координаты x (Q=const); υ не зависит от координаты x (υ=const); gradP не зависит от координаты x (gradP=const); гидродинамическое поле представлено двумя семействами взаимно перпендикулярных прямых линий: изобар и линий тока      P4 P3 P2 P1 P5  |