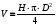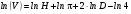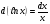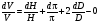Погрешности при измерении физических величин и обработка результатов измерения
 Скачать 181.43 Kb. Скачать 181.43 Kb.
|
|
ПОГРЕШНОСТИ ПРИ ИЗМЕРЕНИИ ФИЗИЧЕСКИХ ВЕЛИЧИН И ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯ Лабораторные занятия по физике имеют целью, во-первых, познакомить Вас с приемами физических измерений и, во-вторых, дать Вам возможность самостоятельно разобраться в ряде основных физических законов. И та, и другая цели достигаются с помощью измерений. Существует два способа измерения физической величины: прямые измерения и косвенные измерения.  Прямыми измерениями называются измерения, в которых результат находится непосредственно в процессе считывания со шкалы прибора (или численных показаний цифровой шкалы прибора). Пример 1. Измерение длины тела с помощью линейки, штангенциркуля или микрометра. Пример 2. Измерение времени падения тела по показаниям механического или электронного секундомера. Косвенными измерениями называются измерения, в которых искомая величина определяется путем расчетов по формуле. При этом вспомогательные величины, входящие в формулу, измеряются прямым способом. Пример 3. Плотность вещества, из которого изготовлен однородный цилиндр, можно измерить следующим образом: прямыми измерениями определить массу цилиндра – m, диаметр цилиндра – d, длину цилиндра – 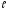 . Тогда плотность найдем по формуле: . Тогда плотность найдем по формуле: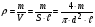 . .Пример 4. Площадь поперечного сечения цилиндрического стержня можно определить по формуле: 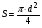 , , при этом диаметр стержня можно измерить прямыми измерениями штангенциркулем или микрометром. При прямом методе измерения физической величины применяют разные методы измерений: технический и лабораторный. При техническом методе искомую величину измеряют однократно. При лабораторном методе одну и ту же величину измеряют многократно одним и тем же прибором, т.е. один и тот же опыт повторяют несколько раз.  Качество средств измерения и результатов измерения принято характеризовать указанием их погрешностей. Правила определения погрешностей прямых и косвенных измерений 1. Абсолютные и относительные погрешности измерений физических величин. Всякое измерение сопряжено с погрешностями. В результате измерения нельзя получить истинного значения измеряемой величины, а возможно лишь определить интервал, в котором лежит истинное значение измеряемой величины.  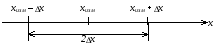 Величину x называют границей абсолютной погрешности, которую, для упрощения терминологии, принято называть абсолютной погрешностью, так как она измеряется в тех же единицах, что и измеряемая величина xизм. Для примера рассмотрим результаты измерений гравитационной постоянной G: G = (6,6720 0,0041) ·10 –11 Н·м2·кг–2 Это значит, что истинное значение G неизвестно, но достоверно (с вероятностью, близкой к 1), можно утверждать, что оно принадлежит интервалу значений: 6,6679·10 –11 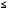 G G 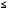 6,6761·10 –11 . 6,6761·10 –11 .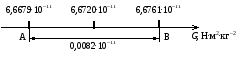 Точки A и B изображают границы абсолютной погрешности измерения. Заметим, что до измерения гравитационной постоянной в 1941 году достоверным считалось значение: G = (6,659 0,005)·10 –11 Н·м2·кг–2, т.е. границы абсолютной погрешности были: 6,654·10 –11 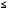 G G 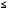 6,664·10 –11; 6,664·10 –11;а с 1941г. по 1980г. достоверным считалось значение: G = (6,670 0,005)·10 –11 Н·м2·кг–2, т.е. границы абсолютной погрешности были: 6,665·10 –11 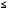 G G 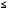 6,675·10 –11. 6,675·10 –11.Абсолютная погрешность не в полной мере характеризует измерение. Качество измерений характеризуется относительной погрешностью, которая равна отношению абсолютной погрешности к значению величины, получаемой в результате измерения. Относительные погрешности выражаются в относительных единицах или в процентах:  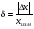 или или 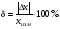 . .Таким образом, относительная погрешность измерения гравитационной постоянной G по современным данным: 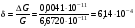 , ,или 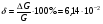 %. %.(До 1941г.: 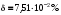 ; до 1980г.: ; до 1980г.: 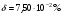 . .Пример 5. При измерении длины стержня установлено, что 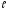 = (100 1) см, а диаметр = (100 1) см, а диаметр 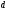 = (2 1) см. Абсолютная погрешность измерения в обоих случаях одинакова, ( = (2 1) см. Абсолютная погрешность измерения в обоих случаях одинакова, (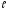 = = 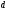 = 1 см), но относительные погрешности составляли: = 1 см), но относительные погрешности составляли: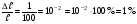 ; ;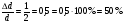 . .Очевидно, что качество измерений длины 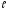 – стержня выше, чем качество измерений d – его диаметра. – стержня выше, чем качество измерений d – его диаметра.2. Определение погрешностей косвенных измероений физических величин. Одним из методов определения погрешностей косвенных измерений, может быть так называемый дифференциальный метод, с которым можно детально ознакомиться в специальной литературе [1, 2]. Согласно этому методу для определения относительной погрешности косвенных измерений следует выполнять три математические операции. Выполним их на примере косвенного определения V – объема цилиндра. Пример 6. Пусть цена деления линейки 1 мм, а измеренные линейкой высота и диаметр цилиндра составили соответственно H = 34 мм, D = 9 мм. Абсолютные погрешности этих измерений равны: H = D = 1 мм. Результаты измерений можно записать в виде: H = (34 1) мм, или H = (3,4 0,1) см, или H = (34 1) · 10 –3 м; D = (9 1) · 10 –3 м. Измеренное значение H имеет две значащие цифры, D – одну. Следовательно, при расчете можно взять число = 3,14. Откуда 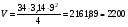 (мм3). (мм3).В примере 6 формула для вычисления объема V:
Шаг 1: возьмем натуральный логарифм от расчетной формулы (1), определяющей искомую величину V:
Шаг 2: найдем дифференциал от левой и правой частей уравнения (1). Напомним, что производная от Ln x – от натурального логарифма x: 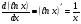 . .Тогда 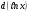 – дифференциал натурального логарифма x равен: – дифференциал натурального логарифма x равен: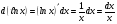 , т.е. , т.е.
Применяя математическую операцию (3) к каждому из членов уравнения (2), получаем:
Шаг 3: все символы d в (4) следует заменить на символы ; символом (греческая буква дельта) обозначают абсолютную погрешность. Тогда расчетная формула для вычисления относительной погрешности будет иметь вид:
В формуле (5), которая является расчетной формулой для вычисления относительной погрешности при косвенных измерениях объема цилиндра, все абсолютные погрешности следует брать по модулю. Следовательно, если в правую часть уравнения (4) входят дифференциалы величин, перед которыми стоит знак минус, то при составлении уравнения (5) следует эти знаки минуса заменить на знак плюс, так как относительная ошибка может только возрастать с ростом количества величин, измеряемых прямым способом. Таким образом относительная погрешность физической величины, определенной путем косвенных измерений (в нашем случае это объем V), равна сумме относительных погрешностей измерений каждой из тех величин, которые входят в формулу для вычисления искомой величины; при этом относительные погрешности физических величин измеряются прямым способом (в нашем случае это H, D). Лабораторный метод измерения и определение погрешностей при измерениях этим методом Причины возникновения и характер проявления погрешностей измерения весьма разнообразны. Поэтому для практических измерений, оказалось, удобно разделить все погрешности на ряд разновидностей, за каждой из которых было закреплено определенное наименование. На сегодня этих наименований около 30!!! Четко усвоить эту терминологию в полном объеме достаточно сложно и доступно лишь высококлассным специалистам по измерениям. Но основные разновидности погрешностей должен хорошо знать и понимать любой специалист с высшим естественно-научным и техническим образованием. 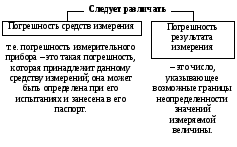 Погрешность результата измерения, конечно, зависит от погрешности средств измерения, но она может отличаться от нее в зависимости от способа измерения (прямое или косвенное измерение), а также от метода измерения (технический или лабораторный метод). Таким образом погрешности средств измерения и погрешности результатов измерений – понятия не идентичные (идентичный (лат.) - одинаковый). Виды погрешностей Различают систематические и случайные погрешности. Систематические погрешности часто связаны с неисправностью прибора (например, изогнута стрелка, и ноль прибора смещен); они сохраняют свою величину и знак от опыта к опыту. Случайные погрешности возникают вследствие самых различных, как субъективных, так и объективных причин (например, плохое освещение шкалы прибора, изменение температуры или напряжение в сети во время опыта и т.д.); они непредсказуемым образом меняют величину и знак погрешности от опыта к опыту.  Погрешность результата многократных прямых измерений (измерения лабораторным методом) Пусть многократные измерения времени падения тела с одной и той же высоты проведены одним и тем же прибором – секундомером, инструментальная погрешность которого составляет ± 0,01 с. В результате измерения лабораторным методом было получено N значений времени падения тела. Будем считать, что число измерений N = 5: 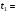 1,01 с, 1,01 с, 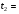 1,02 с, 1,02 с, 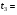 0,99 с, 0,99 с, 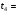 1,03 с, 1,03 с, 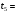 1,00 с. 1,00 с.За наиболее достоверное значение измеряемой величины можно принять среднее арифметическое из всех измеренных значений времени падения: 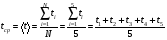 = =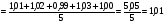 (с). (с).Каждое отдельное измерение ti отличается от среднего арифметического 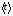 на величину равную на величину равную 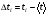 . .Для записи абсолютной погрешности используется символ  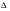 – греческая буква дельта. – греческая буква дельта.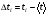 – эти отклонения – эти отклонения 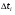 от среднего арифметического значения величины от среднего арифметического значения величины 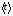 называют абсолютными погрешностями отдельных измерений: называют абсолютными погрешностями отдельных измерений: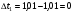 (c), (c), 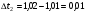 (с), (с),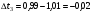 (с), (с), 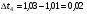 (с), (с),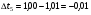 (с). (с).Абсолютную погрешность измерения t – времени (или любой другой величины), полученную лабораторным методом, примем приближенно равной среднему арифметическому значению абсолютных погрешностей отдельных измерений, взятых по абсолютному значению: 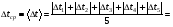 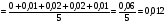 (с). (с).Тогда результат измерений записывается так: 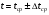 ; ;или в современных обозначениях: 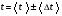 Подставляем результаты вычислений: 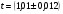 с. с.В такой записи результата измерения содержится ошибка: она состоит в том, что вычисленная абсолютная погрешность измерения, равная 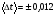 с, с,имеет больше знаков после запятой, чем погрешность измерительного прибора, которым измерялось время: инструментальная погрешность секундомера составляла ± 0,01 с. Поэтому при вычислениях 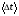 последнюю цифру 2 следует считать сомнительной, т.е. необходимо провести округление, руководствуясь основным правилом округления и правилом вычислений с заранее заданной точностью. последнюю цифру 2 следует считать сомнительной, т.е. необходимо провести округление, руководствуясь основным правилом округления и правилом вычислений с заранее заданной точностью.Т.е. после округления имеем: 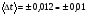 (с). (с).Окончательный результат лабораторного измерения времени падения тела следует записать так: 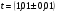 с. с.Эта запись означает, что истинное значение t – времени падения тела находится в пределах: 1,00 с 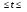 1,02 с. 1,02 с.Основные определения и правила приближенных вычислений 1. Точные и приближенные значения величин (чисел). При решении задач и выполнении лабораторных работ необходимо различать, какие данные точные, какие – приближенные. К точным значениям чисел относятся, например: значения переводных и масштабных множителей, коэффициенты и показатели степени и др. Приближенные значения величин (чисел) получают в результате измерений, округлений и вычислений. При счете могут получаться как точные, так и приближенные значения. Достаточным признаком приближенности результата измерений (или счета) является наличие разных результатов при повторных измерениях (или разных ответов при повторных подсчетах). 2. При вычислениях с приближенными числами их следует записывать, сохраняя лишь верные знаки. Принято считать, что у числа А все знаки верные, если абсолютная погрешность величины A не превышает одной единицы разряда последней цифры числа А. Поясним это утверждение на следующем примере. Пример 7. Пусть число А = 47,813 получено в результате действия над приближенными числами и известно, что относительная погрешность = 0,1%. Найдем абсолютную погрешность: А = 0,047813. Для наглядности сравнения А с А отбрасываем лишние знаки и проводим округление; получаем А = 0,048 и видим, что согласно определению последние цифры числа А (числа 1 и 3) следует считать сомнительными. Значит число А имеет три верных знака. 3. Сомнительными называют последние цифры приближенного значения числа А, если все предшествующие цифры этого значения являются верными. 4. Значащими цифрами числа называют все его верные цифры, кроме нулей, стоящих левее первой отличной от нуля цифры, и нулей, стоящих в конце числа, если они стоят взамен неизвестных или отброшенных цифр при округлении числа. Пример 8. 1). Числа 0,000430 и 10,5 – каждое имеет по три значащих цифры. 2). 1 куб. фут = 0,0283 м3 – содержит три значащих цифры. 3). 1 дюйм = 2,5400 см – пять верных значащих цифр. 5. Незначащие нули чисел слева и справа, как правило, не пишут, их заменяют множителем 10n: например, вместо 13500 записывают 135 ·102. Принято записывать числа в стандартном виде числа. Пример 9. 1). Вместо 13500 = 135 ·102 записывают 1,35 •104. 2). Вместо 0,00043 записывают 4,3 ·10–4. Обратите внимание, что при записи числа в стандартном виде числа сохраняют столько десятичных знаков (знаков после запятой), сколько верных значащих цифр имеет заданное число. Пример 10. 1). В числе 52401 1 верные все знаки. Это число содержит четыре значащих числа, поэтому в стандартном виде числа его следует записать так: 5,240 · 103. 2). В числе 5240 10 верные только первые три знака (последняя цифра – ноль – сомнительная). В стандартном виде число должно быть записано так: 5,24 · 103. Стандартная запись численных значений величин удобна для их оценки по порядку величины, а также для сравнения их численных значений по порядку величины: так числа 1,34 · 104 и 4,3 · 104 совпадают по порядку величины, а числа 1,34 · 104 и 4,3 · 106 отличаются на два порядка (6 – 4 = 2). 6.Округление числа. Если приближенное число содержит лишние (или неверные) знаки, то его следует округлить. При округлении сохраняют только верные знаки, лишние знаки отбрасывают. 7.Основное правило округления: если первая отброшенная цифра равна 5 или больше 5, то последнюю из сохраняемых цифр увеличивают на единицу; если первая отброшенная цифра меньше 5, то последнюю из сохраняемых цифр оставляют без изменения. 8.Правило записи приближенных значений чисел. В приближенных значениях чисел, полученных в результате измерения или вычисления, сохраняют все верные цифры и одну сомнительную, если этот результат является промежуточным, и будет использован в дальнейших вычислениях. То же правило следует применять при записи численных значений взятых из справочных таблиц. Например: g – ускорение свободного падения, G – гравитационная постоянная и т.д. 9. Сложение и вычитание приближенных значений чисел. При сложении и вычитании приближенных значений чисел, в записи которых все цифры верные, оставляют столько десятичных знаков, сколько их имеет приближенное данное с наименьшим числом десятичных знаков. 10. Умножение и деление приближенных значений чисел. При умножении и делении приближенных значений чисел следует в результате сохранять столько значащих цифр, сколько имеет приближенное данное с наименьшим числом верных значащих цифр. 11. Возведение в степень приближенного значения числа. При возведении в квадрат и куб следует в результате сохранять столько значащих цифр, сколько верных значащих цифр имеет возводимое в степень приближенное значение числа. 12. Извлечение корня из приближенного значения числа. При извлечении квадратного и кубического корня следует в результате брать столько значащих цифр, сколько их имеет подкоренное приближенное значение числа. 13. Применение таблицы логарифмов. В значении десятичного и натурального логарифма приближенного значения числа сохраняют столько десятичных знаков, сколько верных значащих цифр имеет заданное число. 14. Вычисление промежуточных результатов. При вычислении промежуточных результатов следует брать одной цифрой больше, чем рекомендуют предыдущие правила подсчета цифр пп. 9 - 13. 15. Предварительное округление более точных данных. Если некоторые данные имеют больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при остальных действиях), чем другие данные, то их предварительно следует округлить, сохраняя лишь одну лишнюю цифру. Пример 11. Табличное значение плотности ртути при температуре 0 °С равна 13,5955 г/см3. Определить массу ртути объемом 25 см3. Решение: m = 13,5955 г/см3 · 25 см3. В соответствии с правилом предварительного округления сохраняем в первом сомножителе три значащие цифры: m 13,6 г/см3 · 25 см3 = 340 г = 0,34 кг. Вычисления без применения этого правила более громоздко, но дает тот же результат: m = 13,5955 г/см3 · 25 см3 = 339,8875 г 340 г 0,34 кг. Если округлить более точное число без лишней цифры, то результат будет менее точным: m 14 г/см3 · 25 см 3 = 350 г. Правила предварительного округления применяют, в частности, тогда, когда используют данные из справочных таблиц. 16. Вычисления с заранее заданной точностью. Если окончательный результат надо получить с некоторой наперед заданной точностью, а данные можно брать с произвольной точностью, то в этих данных следует брать столько цифр, сколько нужно для получения результата с одной лишней цифрой. В окончательном результате эта лишняя цифра отбрасывается. Метрология. Некоторые термины и определения 1. Измерением называют нахождение значения физической величины опытным путем с помощью специальных технических средств. 2. Измерения бывают прямые и косвенные. При прямом измерении искомое значение величины находят непосредственно из опытных данных. Косвенным называют измерение, при котором искомое значение величины находят на основании известной зависимости, между этой величиной и величинами, полученными прямыми измерениями. 3. Мера – средство измерений, предназначенное для воспроизведения физической величины заданного размера. 4. Измерительный прибор – это средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем. 5. Шкала средства измерения – это часть отсчетного устройства, представляющего собой совокупность отметок, соответствующих ряду последовательных значений величины. 6. Отметка шкалы – знак на шкале, соответствующий некоторому значению измеряемой величины. 7. Отсчет – это число, отсчитанное по отсчетному устройству средства измерения. 8. Делением шкалы называют промежуток между двумя соседними отметками шкалы. 9. Ценой деления шкалы называют разность значений величин, соответствующих двум соседним отметкам шкалы. 10. Предел измерений – это наибольшее и наименьшее значения диапазона измерений. 11. Погрешностью измерения называют отклонение результата измерения от истинного значения измеряемой величины. 12. Абсолютная погрешность измерения – это погрешность измерения, выраженная в единицах измеряемой величины. 13 Относительной погрешностью измерения называют отношение абсолютной погрешности измерения к истинному значению измеряемой величины. 14. Важнейшими составляющими погрешности измерения являются инструментальная, систематическая, случайная погрешности и погрешность отсчитывания. 15. Инструментальная погрешность измерения – это составляющая погрешности измерения, зависящая от погрешностей применяемых средств измерений. 16. Систематическая погрешность измерения – это составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. (Например, изначально стрелка прибора установлена не на нулевом делении измерительной шкалы.) 17. Случайная погрешность измерения – составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной той же величины. 18. Погрешность отсчитывания – составляющая погрешности измерения, происходящая – от недостаточно точного отсчитывания показаний средства измерений. 19. Поправкой называют значение величины, одноименной с измеряемой, прибавляемое к полученному при измерении значению величины с целью исключения систематической погрешности. 20. Точность измерений – это качество измерений, отражающее близость их результатов к истинному значению измеряемой величины. Количественно точность измерений может быть выражена обратной величиной модуля относительной погрешности. Описание технических средств измерения Штангенциркуль Штангенциркуль является более точным измерительным прибором по сравнению с метрической линейкой. Его паспортные данные – пределы измерения и инструментальная погрешность прибора – выбиты на поверхности штангенциркуля. Более высокая точность штангенциркуля обеспечивается линейным нониусом. Штангенциркуль (рис.1.) состоит из миллиметрового масштаба М (шкалы прибора), жестко связанного со щекой АА'. N – линейный нониус представляет собой небольшую линейку, нанесенную на подвижную щеку ВВ'. При сомкнутых щеках AA' и BB' нулевые отметки шкалы нониуса и масштабной линейки совпадают. Для промера наружных размеров измеряемый предмет вводят между щеками AB, которые сдвигаются до соприкосновения с предметом; затем закрепляют подвижную щеку BB' зажимом C и производят отсчет. Число целых миллиметров отсчитывается непосредственно по шкале M прибора до нулевой метки нониуса. Число долей миллиметра отсчитывают по нониусу, пользуясь следующими правилами. 1) Находим метку нониуса, совпадающую с какой-либо меткой шкалы M прибора (на рис. 1 - это вторая метка). 2) Умножаем номер метки нониуса, совпадающей с меткой шкалы прибора, на инструментальную погрешность прибора, выбитую на его поверхности. Полученное произведение дает число долей миллиметра: 2 • 0,1 мм = 0,2 мм. Результатом измерения является сумма показаний, снятых со шкалы прибора и шкалы нониуса. В примере на рис.1. диаметр детали, измеряемой щеками АВ, равен: D = 8 мм + 0,2 мм = 8,2 мм. При однократном измерении погрешность измерения равна инструментальной погрешности измерения. Тогда результат измерения, учитывающий абсолютную погрешность, следует представить так: D = (8,2 0,1) мм или D = (8,2 0,1) · 10–3 м. Относительная погрешность: 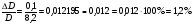 Стандартные приборы с линейным нониусом позволяют производить измерения с точностью от 0,1 до 0,01 мм. Для измерения диаметров внутренних отверстий и других внутренних промерах используются щеки A'В'. Отсчет результата производится по тем же правилам, что и при измерении щеками AВ (на рис.1. диаметр отверстия d также равен 8,2 мм). При измерениях H – глубины отверстий в деталях применяют рейку F, которая вдвигается в отверстие до упора (на рис.1. глубина отверстия H также равна 8,2 мм). 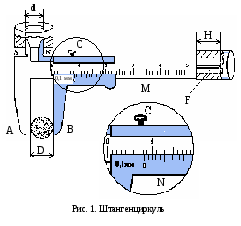 Микрометр Микрометр обычно представляет собой массивную металлическую скобу (см. рис. 2), на концах которой находятся друг против друга неподвижный упор А и упор B, жестко связанный с микрометрическим винтом W. Микрометрическим винтом называют винт, шаг которого достаточно постоянен по всей длине винта. Шагом винта называют величину поступательного перемещения конца винта при повороте его на один оборот. Для измерительных целей микрометрический винт снабжается особой головкой с делениями, называемой обычно барабаном. Барабан С, жестко связанный со стержнем B, делится на 50 делений. Поворот на одно деление соответствует смещению стержня на 0,01 мм. С этой точностью обычно производят измерения с помощью микрометра, т.е. инструментальная погрешность такого микрометра равна 0,01 мм. Поступательное перемещение винта измеряется по смещению среза барабана вдоль оси D. Шаг винта равен 0,5 мм, т.е. за один полный оборот барабана винт поступательно перемещается на 0,5 мм и расстояние между упорами А и В изменяется на 0,5 мм. Для измерения размера детали необходимо, осторожно вращая барабан с помощью головки E, зажать деталь между упорами А и В. Вращение головки Е вызывает перемещение винта, а следовательно упора В. ВНИМАНИЕ !!! Результаты измерения зависят от того, с какой силой сжимается измеряемый объект микрометром. Винт с малым шагом превращает небольшое усилие руки, поворачивающей барабан микрометра, в большие силы, которые действуют на предмет и деформируют его. Чтобы уменьшить ошибку, связанную со слишком сильным (и неодинаковым в разных опытах) сжатием измеряемых предметов, рукоятка микрометра снабжена специальной головкой Е (трещоткой). Это устройство позволяет создавать при измерениях небольшое и постоянное в разных опытах давление на измеряемый предмет. Осторожно вращайте микрометрический винт только за головку Е (трещотки). Иначе вы можете "сорвать" резьбу и испортить прибор. После того, как деталь будет зажата между упорами А и В, производят отсчет ее размера. Число целых миллиметров измеряется по шкале D до среза барабана винта, а доли миллиметра отсчитываются по шкале барабана С до продольной метки, пересекающей шкалу D. Прочитайте показание микрометра на рис. 2: (8 + 0,5 + 0,29) мм = 8,79 мм. Расстояние между упорами А и В: d = (8,79 0,01) мм. 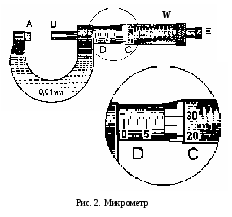 |