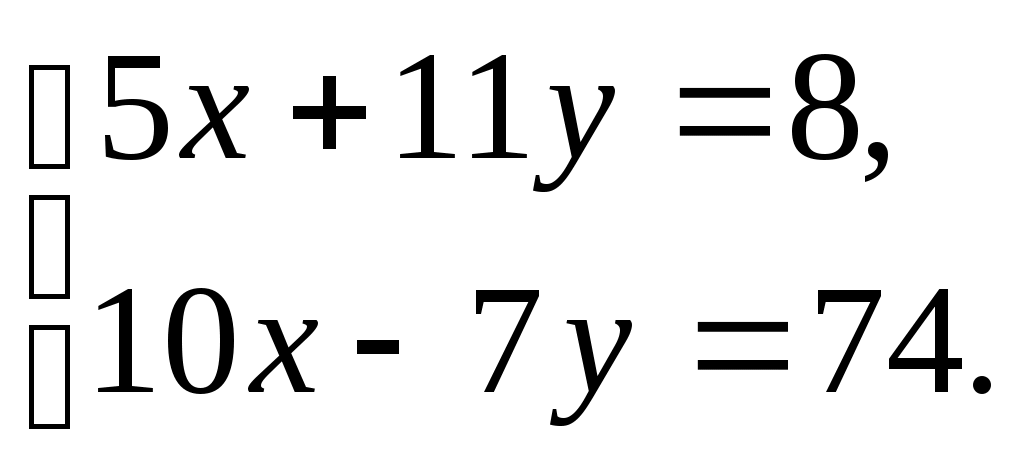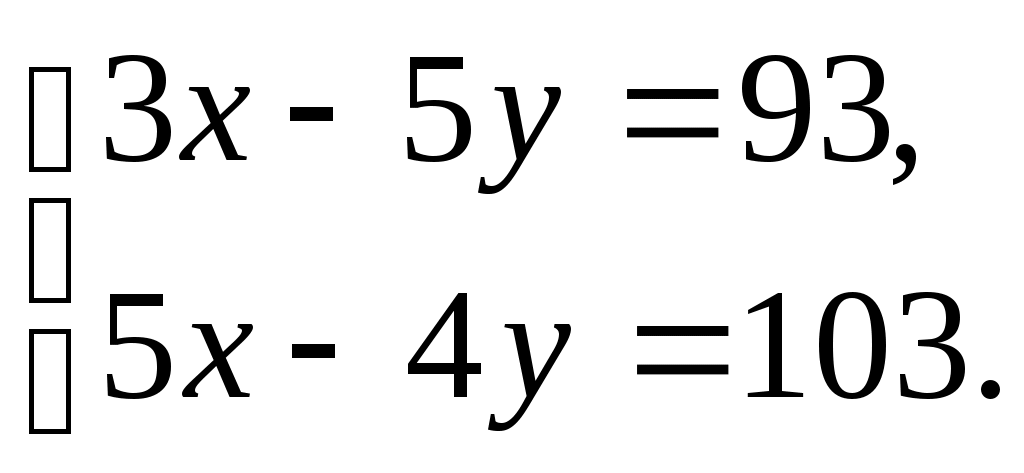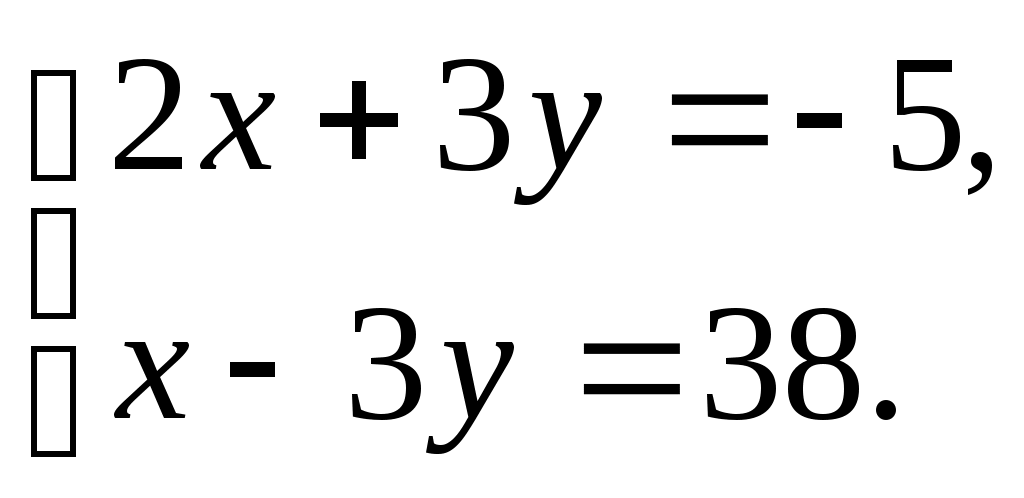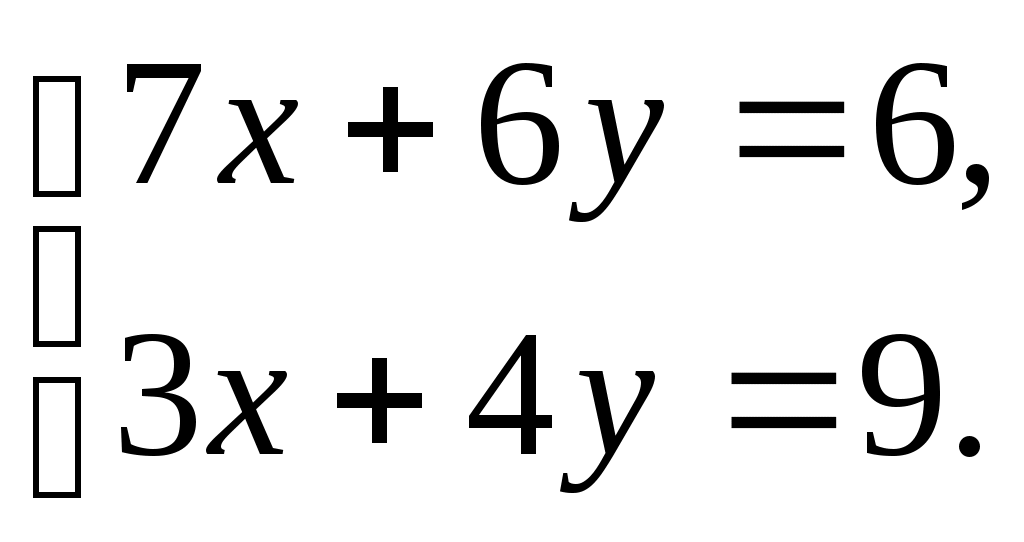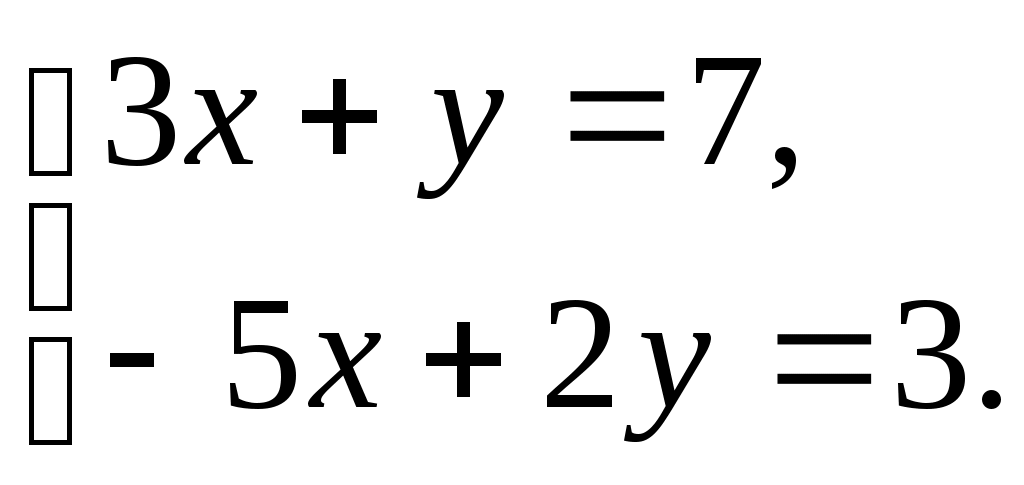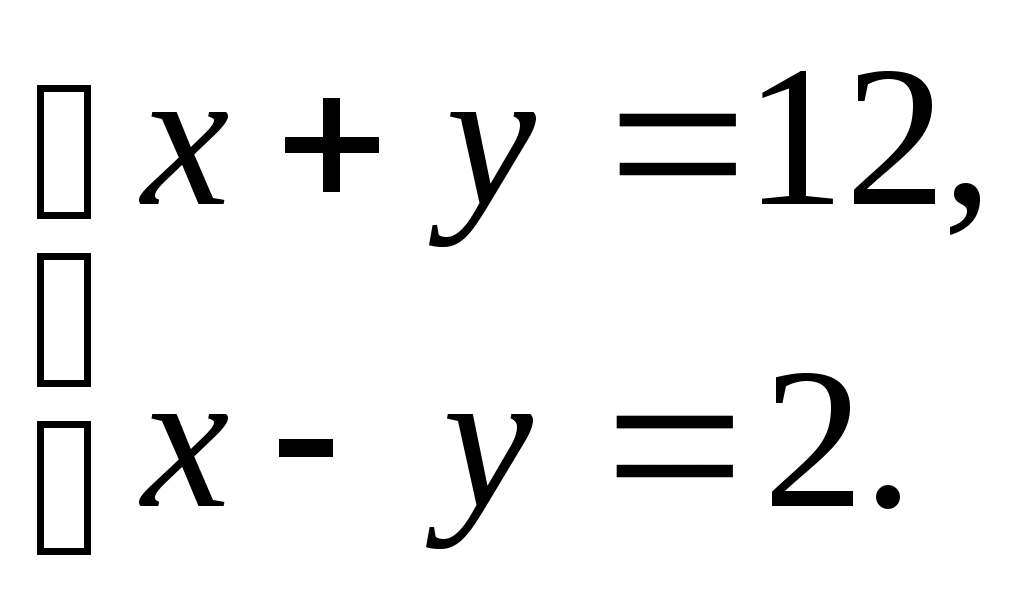выступление на педсоветеПоложительное влияние познавательного интереса на мотивацию учебной деятельности и на результативность у. Выступление на педсовете. Положительное влияние познавательного интереса на мотивацию учебной деятельности и на результативность учебного процесса
 Скачать 131.5 Kb. Скачать 131.5 Kb.
|
|
Выступление на педсовете 24.12.2015. «Положительное влияние познавательного интереса на мотивацию учебной деятельности и на результативность учебного процесса» Современное общество предъявляет высокие требования к выпускникам: интеллектуальность, грамотность, высокие и прочные знания. Однако, успех в решении учебных и воспитательных задач на уроках в значительной мере определяется интересом к предмету. Если учащимся нравятся уроки математики, то учебный процесс идет легко, знания , умения и навыки учеников отличаются прочностью и глубиной. Активизация познавательной деятельности ученика без развития его познавательного интереса не только трудна, но и практически невозможна. Между тем известно, что математика как школьный предмет не всегда пользуется популярностью среди учеников. Так, количество учащихся, называющих математику в числе любимых предметов, нередко составляет лишь 7-10%. Интерес к математике у старших подростков значительно снижается, а количество высказываний о безразличии к математике как к предмету возрастает от класса к классу. Эти факты лишний раз свидетельствуют о том, что проблема пробуждения и развития интереса к изучению математики является одной из наиболее серьезных в современной методике. Проблема интереса – это не только вопрос о хорошем эмоциональном состоянии детей на уроках, от ее решения зависит, будут ли в дальнейшем накопленные знания мертвым грузом или станут активным достоянием школьников. Многочисленные исследования показали, что интерес стимулирует волю и внимание, помогает более легкому и прочному запоминанию. Однако значение познавательного интереса выходит далеко за рамки учебного процесса. В триединой задаче: обучения, умственного развития и воспитания личности – интерес является связующим звеном между тремя ее сторонами. Именно благодаря интересу, как знания, так и процесс их приобретения могут стать движущей силой развития интеллекта и важным фактором воспитания. О большом влиянии на развитие интеллекта говорил известный советский психолог А.Н. Леонтьев: «То, для чего открыто сердце, не может составить тайны и для разума». Интерес не только способствует развитию интеллекта, но и является одной из движущих сил личности в целом, интерес содействует формированию волевых качеств личности, а также укреплению ее активной жизненной позиции. Также замечено, что люди, проявляющие поисковую активность, заболевают гораздо реже, чем люди, лишенные такой активности по тем или иным обстоятельствам. Интерес положительно влияет на все психические процессы и функции. Особенно велика связь интереса с вниманием. « Кто интересуется предметом, у того открыты глаза и уши», - говорил один немецкий педагог. Внимание, связанное с интересом, бывает длительным и глубоким. Огромное влияние интереса и на память: интересное запоминается легко, быстро и прочно. Интерес способствует значительному повышению работоспособности. Вот почему важное место в комплексе основных задач обучения занимает проблема формирования познавательного интереса. Познавательный интерес – избирательная направленность личности на предметы и явления окружающей действительности. Эта направленность характеризуется постоянным стремлением к новым, более полным и глубоким знаниям. Систематически укрепляясь и развиваясь, познавательный интерес становится основой положительного отношения к обучению. Познавательный интерес – это одно из личностных свойств ученика, черта его характера, проявляющаяся в виде пытливости, любознательности, активности. С одной стороны, познавательный интерес есть источник обеспечения воспитательных задач обучения, обогащающий и направляющий поступки ученика, с другой стороны, познавательный интерес есть результат воспитательных воздействий, способствующий процессу освоения и добывания знаний по тому или иному учебному предмету. Познавательный интерес: - способствует более свободному приобщению личности к общественным ценностям. - находясь у основания творческой деятельности, он стимулирует выбор личных ценностей - создаёт благоприятные условия для развития активности и самостоятельности учащихся, нейтрализуя равнодушие и инертность Интерес, как мотив оказывает воздействие на воспитание морально-волевых черт личности. Познавательный интерес носит поисковый характер. Под его влиянием у ученика постоянно возникают вопросы, ответы на которые он сам активно ищет. При этом поисковая деятельность учащегося совершается с увлечением, он испытывает эмоциональный подъем, радость от удачи. Познавательный интерес положительно влияет не только на результат деятельности, но и на протекание психических процессов – мышления, воображения, памяти, внимания, которые под его влиянием приобретают особую активность и направленность. При правильной педагогической организации деятельности учащихся, интерес может и должен стать устойчивой чертой личности. В настоящее время, особенно важно формировать интерес учащихся к процессу познания, к способам поиска, усвоения, переработки и применения информации, что позволило бы им легко ориентироваться в современном быстро изменяющемся мире. Успех развития познавательной потребности зависит от умения преподавателя поставить перед учащимися доступные им, и в то же время требующие активной мыслительной деятельности познавательные задачи. Ученые считают, что результаты деятельности человека на 20-30 % зависят от интеллекта, и на 70-80 % - от мотивов. В современной школе вопрос о мотивации учения без преувеличения может быть назван центральным, так как мотив является источником деятельности и выполняет функцию побуждения и смыслообразования. Необходимо понимать общую структуру мотивации к учению: а) Познавательная мотивация Глубокий интерес к изучению какого-либо учебного предмета встречается редко, но хорошо успевающих детей привлекают разные, в том числе самые сложные учебные предметы. Если ребенок в процессе обучения начинает радоваться тому, что он что-то узнал, понял, чему-то научился, - значит, у него развивается мотивация, соответствующая структуре учебной деятельности. К сожалению, даже среди хорошо успевающих учеников крайне мало детей, имеющих учебно-познавательные мотивы. Ряд современных исследователей прямо считают, что причины, объясняющие, почему у одних детей есть познавательные интересы, а у других их нет, следует искать, прежде всего, в самом начале школьного обучения. Человек обогащается знаниями только тогда, когда эти знания для него что-то значат. Одна из задач школы – преподавать предметы в такой интересной и живой форме, чтобы ребенку самому захотелось изучать их и запомнить. Изучение только по книгам и при помощи бесед довольно ограничено. Предмет постигается гораздо глубже и быстрее, если его изучают в реальной обстановке. Чаще всего познавательные интересы формируются чисто стихийно. В редких случаях у одних вовремя рядом оказывается папа, книга, дядя, у других – талантливый учитель. Однако проблема закономерного формирования познавательного интереса и у большинства детей остается нерешенной. б) Мотивация достижения успеха. У детей с высокой успеваемостью ярко выражена мотивация достижения успеха — желание хорошо, правильно выполнить задание, получить нужный результат. В начальных классах эта мотивация нередко становится доминирующей. Мотивация достижения успеха, наряду с познавательными интересами, — наиболее ценный мотив, ее следует отличать от престижной мотивации. в) Престижная мотивация . Престижная мотивация характерна для детей с завышенной самооценкой и лидерскими наклонностями. Она побуждает ученика учиться лучше одноклассников, выделиться среди них, быть первым. Если престижной мотивации соответствуют достаточно развитые способности, она становится мощным двигателем развития отличника, который будет на пределе своей работоспособности и трудолюбия добиваться наилучших учебных результатов. Индивидуализм, постоянное соперничество со способными сверстниками и пренебрежительное отношение к остальным искажают нравственную направленность личности таких детей. Если же престижная мотивация сочетается со средними способностями, глубокая неуверенность в себе, обычно не осознаваемая ребенком, наряду, с завышенным уровнем притязаний приводят к бурным реакциям в ситуациях неуспеха. г) Мотивация избегания неудачи. У неуспевающих учеников престижная мотивация не развивается. Мотивация достижения успеха, а также мотив получения высокой оценки характерны для начала обучения в школе. Но и в это время отчетливо проявляется вторая тенденция — мотивация избегания неудачи. Дети стараются избежать «двойки» и тех последствий, которые влечет за собой низкая отметка, — недовольства учителя, санкций родителей. д) Компенсаторная мотивация. К этому времени у неуспевающих детей возникает и особая компенсаторная мотивация. Это побочные по отношению к учебной деятельности мотивы, позволяющие утвердиться в другой области — в занятиях спортом, музыкой, рисованием, в заботах о младших членах семьи и т.п. Когда потребность в самоутверждении удовлетворяется в какой-то сфере деятельности, низкая успеваемость не становится источником тяжелых переживаний ребенка. Как развивать у школьника интерес к предмету? Щукина Г.И., одна из ведущих разработчиков проблемы формирования интереса в процессе учебы считает, что интересный урок можно создать за счет следующих условий: личности учителя (очень часто даже скучный материал, объясняемый любимым учителем, хорошо усваивается); содержания учебного материала (когда ребенку просто нравится содержание данного предмета); методов и приемов обучения. Если первые два пункта не всегда в нашей власти, то последний – поле для творческой деятельности любого преподавателя. Само по себе содержание обучения, учебная информация вне потребностей учащихся не имеет для них какого-либо значения, а следовательно, не побуждает к учебной деятельности. И поэтому учебный материал должен подаваться в такой форме, чтобы вызвать у учащихся эмоциональный отклик, активизировать познавательные психические процессы. Для этого необходимы: 1. Особый подход к освещению учебного материала, характер его преподнесения; 2. Использование, показ, выделение различных элементов, привлекательных сторон содержания; 3. Задания с интересным содержанием, занимательными вопросами. 4. Показ значимости знаний, умений: 5. Межпредметные связи.(связь теории с практикой, с физикой, химией, экологией, экономикой, историей, социологией, статистикой) Проблема, которая встает при этом для меня - это разработка собственной системы развития мотивации учения, развития познавательного интереса как глубинного мотива учения, создание эффективной системы отслеживания мотивации образовательной деятельности. В математике столько серьёзного, способного заинтересовать и увлечь учащихся, что она по своим возможностям в развитии математического мышления может поспорить со многими предметами школьной программы. Прелесть решения занимательных задач, парадоксов, фокусов, раскрытие головоломок и софизмов и т.д. должен испытать каждый учащийся. Даже развлекательность может быть частично использована для того, чтобы помочь понять своеобразие "сухой" науки. Нужно позаботиться о том, чтобы каждый ученик, работал активно и увлеченно, и это использовать как отправную точку для возникновения и развития пытливости, любознательности, глубокого познавательного интереса. Внеклассная работа по математике должна быть массовой по охвату и познавательной, активной, творческой относительно деятельности учащихся. Игры и игровые формы должны включаться не для того, чтобы развлечь учащихся, а чтобы возбудить у них стремление к преодолению трудностей. Цель введения их состоит в том, чтобы удачно соединить игровые и учебные мотивы и в такой деятельности постепенно сделать переход от игровых мотивов к учебным, познавательным. Стимулирование познавательного интереса можно разделить на два вида: по содержанию и по методам учебной деятельности. Стимулы действуют во взаимосвязи, и в различных классах и в составе различных предметов имеют свою модификацию и по-разному влияют на интерес. К побуждающим стимулам содержания обучения относятся: новизна учебного материала, исторический подход к содержанию знаний, обновление уже усвоенных знаний, практическая значимость содержания знаний. Новизна содержания материала. Действие нового, ещё не бывшего в опыте элемента знаний осознаётся как факт, содействующий либо возникновению, либо укреплению познавательного интереса. При этом элемент новизны важный фактор поддержания познавательного интереса в процессе обучения вообще. Элемент новизны, внесенный во все стороны учебного процесса, всегда оказывает побуждающее действие (новые факты, новые сравнения, новый аспект подачи нового материала, новые формы деятельности, новые способы решения задачи). Наиболее важными состояниями человека, сопровождающими процесс его активной ориентировки являются состояния неожиданности, озадаченности, удивления. Новизна и есть тот стимул внешней среды, который возбуждает эти состояния. Стимул новизны находит своё выражение также в содержании, выходящем за пределы программы. Это желание развить кругозор учащихся, приобщить их к широкой жизни, более основательно подкрепить воспитательный процесс. Новизна в первую очередь связана с содержанием информации и способами её подачи. Особенно необходимо это учитывать в IV-V классах, так как в этом возрасте школьники всё ещё выясняют, кто из них самый-самый. Поэтому в этих классах в начале урока, как правило, даются различные примеры на проявление наблюдательности, внимания, выдумки, фантазии. Выбор формы изложения нового материала находится целиком во власти учителя, зависит от его знаний, умений, мастерства, от его вкуса. При этом нельзя не учитывать, что ребята быстро привыкают к одному методу преподавания и устают от однообразия организации их деятельности на уроке, а новое начало позволит избежать этого, даже если вся остальная часть урока построена традиционно. Перечислим лишь некоторые способы организации начала урока. 1.Предлагается задача, которая решается только с опорой на жизненный опыт ребят, на их смекалку. 2. Даётся задача на тренировку памяти, наблюдательности, на поиск закономерностей по материалу, хорошо усвоенному школьниками. 3. На доске записаны уравнения или числовые выражения, или неравенства и ответы к ним, среди которых есть как верные, так и неверные. Предлагается проверить их. 4. Даётся обычная традиционная задача с традиционным решением. Предлагается найти более короткое, рациональное решение. 5. Обсуждаются различные способы решения задачи, заданной на предыдущем уроке. Как правило, это задача, решение которой требует исследовательской работы. Однако она должна быть необычной, интересной, но доступной для всех учащихся. 6. Если же на дом было задано сочинить сказку или составить математический кроссворд, или ребус, или математическую задачу, то естественно начинать урок с представления наиболее удачных работ. 7. Рассматривается некоторая математическая проблема, которая ещё не обсуждалась в классе. Ученики намечают план поиска её решения. Учителю, проводящему урок в 5 классе по теме « Градусная мера углов», рекомендуем урок начать с прочтения стихотворения: У человека два плеча, Оля, Таня и Вова А в сутках день, да ночка. Отличаются ростом. Углом назвали два луча Угол меньше прямого С началом в общей точке. Называется острым. Затем учитель организует фронтальную работу с учащимися Следует предложить ученикам модели углов и попросить ответить на вопросы : « Вопрос 1. Как называется инструмент, с помощью которого измеряются углы? (Транспортир). Вопрос 2. Чему равна сумма углов, которые вам показаны? ( 400+700=1100). А теперь вычислим сумму трёх углов. Каждому ученику раздаются по одному треугольнику. Ребята убеждаются, что у всех треугольники разного вида . Задание (записано на доске). 1. Отрываем углы у треугольника и складываем. 2. Находим сумму оторванных углов. 3. Какой угол мы получили? (Развёрнутый). 4. Чему равна градусная величина этого угла? (180о). Очевидно, в древности ученые также как и мы пришли к этому выводу практическим путём. А в 7 классе мы докажем, что сумма всех углов треугольника равна 180о, используя те знания из геометрии, что нам уже знакомы». При организации фронтальной работы в 8 классе в начале урока по теме: "Что такое функция" можно дать такое задание: "Решить анаграммы и исключить лишнее слово: ачазда, пемеренаня, уеренавни, цияфунк. Рассуждения учащихся следующие: исходные слова – задача, переменная, уравнение, функция. Задачу можно решить с помощью уравнения, содержащего переменную. Значит, лишним будет слово "функция". Сразу же возникает вопрос "Что такое функция?" Таким образом, можно перейти к изложению нового материала. По мнению многих педагогов, эффективным средством формирования познавательного интереса является противоречие между новой информацией и имеющимися знаниями. Причём, чем выше степень несоответствия, тем сильнее ожидается познавательная активность учащихся. Но, исследования доказывают, что познавательный интерес возникает тогда, когда для объяснения нового явления могут быть использованы уже имеющиеся знания и прошлый опыт. Непонятное, хотя и привлекает внимание учащихся, вызывает ситуативный, временный интерес, который может быстро исчезнуть. Обновление уже усвоенных знаний. Любая получаемая человеком информация интересна для него только тогда, когда в ней есть и новое, и старое, уже знакомое. Совершенно незнакомое будет непонятным и, следовательно, неинтересным, а старое без элемента новизны не привлечет внимания. Новое, незнакомое интересно тогда, когда в опыте человека уже есть что-то такое, с чем это новое можно сопоставить. Понимание и есть установление связи известного с ещё неизвестным, но актуальным. Чем теснее связаны старые и новые знания, чем более увязываются они в единую систему, тем больше шансов, что учебные материал будет понятным и интересным. Новое усваивается легко и с интересом тогда, когда оно вплетено в контекст всех ранее усвоенных знаний и сложившихся представлений, когда оно пробуждает свежие ассоциации по поводу того, что уже казалось понятным и знакомым. "Это значит, что процесс обучения должен строиться так, чтобы новое дополняло картину мира, а не разрушало её". Оно должно многочисленными ассоциативными связями прирастать к ранее известному, обретать в этом ране известном почву и одновременно удобрять её и подпитывать. Однако маловероятно, что это может происходить само собой, без усилий со стороны педагога". Историзм. Математика и история - две неразрывные области знания. Сведения из истории математики, исторические задачи сближают эти два школьных предмета. История обогащает математику гуманитарным и эстетическим содержанием, развивает образное мышление учеников. Математика, развивающая логическое и системное мышление, в свою очередь занимает достойное место в истории, помогая лучше ее понять. Вопрос об использовании элементов истории в преподавании математики не новый. Ещё в конце XIX века он обсуждался на съездах учителей математики. Основные цели исторического материала следующие: Повышение интереса учащихся к изучению математики и углубления понимания ими изуаемого фактического материала. Расширение умственного кругозора учащихся и повышение общей культуры. Формы подачи исторического материала могут быть различными, начиная от простых (беседа учителя, короткие сообщения учеников на заданную тему, решение исторических задач, разгадывание софизмов, выпуск стенгазет) до более глубоких и сложных – таких как историко-математическая конференция, защита рефератов по вопросам истории математики. И все-таки опытный учитель никогда не начнет изложения новой темы, не говоря о новом разделе математики, без вводной исторической части, вызывающей интерес и внимание учеников. Залог успеха состоит в умелом использовании элементов истории математики таким образом, чтобы они органически сливались с излагаемым фактическим материалом. Большую методическую трудность представляет решение вопроса об отборе конкретного материала по истории математики и о порядке его использования в том или другом классе. Здесь следует руководствоваться программой по математике. Однако, учитывая возрастные особенности учащихся, нельзя приспосабливаться только к программе. Не только содержание и объем, но и стиль изложения из истории математики не могут быть одинаковыми в разных классах. Какая бы ни была форма сообщения сведений по истории – краткая беседа, экскурс, лаконичная справка, решение задачи, показ и разъяснение рисунка – использованное время (5-12 мин.) нельзя считать потерянным, если только учитель сумеет исторический факт преподнести в тесной связи и излагаемым на уроке теоретическим материалом. Историческая справка должна удовлетворять следующим требованиям: 1. Показать возникновение математического понятия из нужд и потребностей человека. 2. Процесс развития математического понятия. 3. Область применения этого понятия в настоящее время. Практическая значимость содержания знаний. Стимуляция познавательного интереса при помощи показа практической значимости знаний, чрезвычайно актуальна для младших подростков, которые в силу недостатка знаний и опыта не всегда оценят теоретическую ценность и значимость получаемых знаний, но всегда охотно откликаются на возможность практически использовать знания в своей личной жизни. Поэтому, рекомендуем учителям на уроках использовать для решения практически значимые, часто встречающиеся в быту задачи. Форма работы с учащимися может быть как групповой, так и фронтальной. В качестве примера приведем отрывок из урока математики в 8 классе. Тема: "Формула площади прямоугольника". Цель: обеспечить повторение материала темы, способствовать формированию умения перенести знания в новую ситуацию. Развитие познавательного интереса через стимулы, связанные с организацией и характером протекания учебной деятельности учащихся К стимулам, связанным с организацией познавательной деятельности учащихся, относятся: многообразие форм самостоятельной работы учащихся; владение ими новыми способами познавательной деятельности; проблемность в обучении; элементы исследования; различные творческие и практические работы. Самостоятельные работы. Самостоятельная работа в обучении математике не самоцель. Она необходима для перевода знаний извне во внутреннее достояние учащегося, необходима для овладения этими знаниями, а также для осуществления контроля со стороны учителя за их усвоением. Самостоятельные работы являются также необходимым условием развития учащихся, воспитания самостоятельности и познавательной активности учащихся, привития навыков учебного труда и т.д. Особое место в ряду этого вида стимулирования занимает проблемность. Учитель может сообщить учащимся знания в готовом виде, но это не создаст той актуализации в сознаниях, переживаниях школьника, которая возникает при проблемном обучении. Проблемность. К проблемному обучению вновь и вновь возвращается наука и практика обучения. Это объясняется, с одной стороны, пониманием преимуществ такого обучения, с другой, - трудностью его организации на практике, отсутствием соответствующих технологий. Организуя индивидуальную работу учащихся при изучении темы « Иррациональные числа» в 8 классе можно порекомендовать учителю смоделировать следующую проблемную ситуацию: В начале урока, наряду с другими заданиями устного счета, дается задача: «Вычислить площадь квадрата со стороной 10см2; 12 см2; 1,5 см2». И тут же, после решения этой задачи, предлагается учащимся решить обратную задачу: «Найти длину стороны квадрата площадь которого равна 25см2; 1,44см2; 2см2». Предлагается объяснить прием вычисления. Когда учащиеся подходят к последнему значению, наступает тишина, даже сильные ребята не могут дать ответ сразу. Ведь вычислять квадратные корни из простых чисел они не умеют. Озадачили их? Напряжение передается и слабым. Все активно включаются в работу. Начинают думать, рассуждать, открывать для себя новое. У каждого возникает вопрос «Как?». А раз есть подобный вопрос, значит, появляется желание узнать, научиться. А это желание – залог успешного освоения нового. В тесной связи с проблемностью в качестве стимула выступает исследовательский подход, приобщение учащихся к методам науки. Элементы исследования. Учебное исследование – это не только познавательная деятельность учащихся под руководством учителя, но и метод обучения самой исследовательской деятельности. Приобщение к ней делает учёбу производительным трудом, повышает развивающий эффект обучения, который состоит и в приобретении новых знаний, и в овладении новыми способами деятельности. В школьных учебниках, как правило, излагаются соответствующие программе фрагменты математических теорий, т.е. готовые системы знаний. Проблема состоит в том, чтобы в процессе обучения смоделировать потенциальную исследовательскую деятельность, результатом которой являются эти знания. Целями обучения геометрии является не только усвоение школьниками содержания знаний, геометрического материала, но и способов их получения, формирование представление о методах работы с геометрическими объектами. Освоение учениками общих приемов работы с геометрическим материалом дает возможность ученикам самостоятельно включаться в познавательную деятельность, дает независимость от учителя в поиске новых знаний, способность самостоятельно осуществлять учебные исследования. В. В.Давыдов считает, что обучение в школе нужно строить так, чтобы оно повторяло процесс рождения и становления новых знаний. В процессе организованной таким образом учебно-познавательной деятельности "школьники осуществляют мыслительные действия, адекватные тем, посредством которых исторически вырабатывались эти продукты духовной культуры", т.е. становятся "учениками - исследователям". Ученику более интересно и более естественно проводить исследование (квазиисследования), открывая для себя новые факты, чем выучивать готовый фактический материал Ученик, способный проводить учебное исследование, может самостоятельно, или частично самостоятельно, выбрать объект для исследования и изучит его свойства в рамках своих учебных возможностей. Для этого мотивы освоения учениками приемов математического исследования должны стать ведущими и послужить целям формирования интереса не только к учебно-познавательной, но и к учебно-поисковой и учебно-исследовательской деятельности. В 8 классе этот метод можно реализовать при изучении темы «Четырехугольники». Задача. Доказать, что во всяком четырехугольнике середины его сторон служат вершинами параллелограмма. Развитие познавательных интересов учащихся самым непосредственным образом связано с развитием их творческой активности. Творческие работы. Математика в своей серьёзности достаточно таинственна и романтична. В преподавании этого предмета господствует собственный язык математики. Но интеллектуальный и эстетический заряд школьного урока математики, его впечатляемость значительно повышаются, когда учитель не пренебрегает разнообразными приёмами образно-эмоционального аккомпанемента, расцвечивающего прямую научную информацию. Почему бы учителю математики на уроке, а также и при других формах общения с учащимися к месту и в меру не воспользоваться, например, стихотворной цитатой, изящной шуткой и остротой, занимательной задачей, игровыми элементами как средством возбуждения в сознании учащихся "чувствуемой мысли". На уроках математики можно предложить ученикам выполнить творческие задания по теме. Например: составить задачи на тему "Десятичные дроби", написать сказку на тему "Положительные и отрицательные числа", составить кроссворд на тему "Окружность", построить фигуру на тему "Координатная плоскость" и найти загадку к этой фигуре, составить ребус на тему "Многочлены» и т.п. С помощью таких заданий, которые используются на последующих уроках, удается изгнать скуку, равнодушие. При этом нужно помнить, что создание положительных эмоций у школьников – мощный инструмент их обучения и воспитания. Так, с учениками 8 класса на уроке геометрии по теме «Окружность» рекомендуем разыграть сказку под названием «В стране треугольников». « Собрались однажды треугольники и решили выяснить: кто из них главнее всех.Например, в 6 классе. Тема: "Координатная плоскость". Учащимся учитель предлагает выполнить следующее задание: "Построить по заданным координатам фигуру". Загадка. "Весь день рыбак в воде стоял, мешок рыбешкой набивал. Закончив лов, забрал улов, Поднялся ввысь – и был таков". (4;0), (1;3), (2;4), (2;6), (3;7), (7;8), (8;8), (7;7), (8;7), (7;6), (8;6), (7;5), (8;5), (7;4), (9;5), (9;3), (7;0), (-1;0), (-2;2), (-2;4), (0;8), (-2;6), (-3;6), (-5;8), (-1;8), (-5;9), (-1;9), (0;10), (1;10), (2;9), (0;6), (0;4) Глаз (0;9), клюв (-1;9), (0;8). И в качестве домашнего задания предложить учащимся составить аналогичную задачу. Большое значение для развития интереса имеет показ учителем лучших тетрадей, творческих работ, образцов работ. Все это воодушевляет учащихся, позволяет им видеть те вершины, к достижению которых они должны стремиться. Одной из форм обучения учащихся математике, способствующей развитию и воспитанию ценных графических, вычислительных навыков и умений, являются практические работы. При этом первостепенное значение имеет выработка практических навыков владения черчением. Практическая работа. Нетрадиционные формы урока. Существует несколько разновидностей нетрадиционных форм урока, каждая из которых решает свои образовательные задачи. Однако все они преследуют общую цель: поднять интерес учащихся к учёбе и к математике и, тем самым, повысить эффективность обучения. Многие нетрадиционные формы уроков по объёму и содержанию рассматриваемого на них материала нередко выходят за рамки школьной программы и предполагают творческий подход со стороны учителя и учащихся. Немаловажно, что все участники нетрадиционной формы урока имеют равные права и возможности принять в нем самое активное участие, проявить собственную инициативу. Нетрадиционные формы урока можно рассматривать как одну из форм активного обучения. Это попытка повышения эффективности обучения, возможность свести воедино и осуществить на практике все принципы обучения с использованием различных средств и методов обучения. Для учащихся нетрадиционный урок – переход в иное психологическое состояние, это другой стиль общения, положительные эмоции, ощущение себя в новом качестве (а значит, новые обязанности и ответственность). Такой урок дает возможность развивать творческие способности и личностные качества, оценить роль знаний и увидеть их применение на практике, ощутить взаимосвязь разных наук; это самостоятельность и совсем другое отношение к своему труду. Для учителя нетрадиционный урок, с одной стороны, - возможность лучше узнать и понять учеников, оценить их индивидуальные особенности, решить внутриклассные проблемы (например, общения); с другой стороны, это возможность для самореализации, творческого подхода к работе, осуществление собственных идей. Подготовка и проведение урока в любой нетрадиционной форме состоит из четырёх этапов: 1- замысел, 2 – организация, 3 – проведение, 4 – анализ. Увеличение умственной нагрузки на уроках математики заставляет задуматься над тем, как поддержать у учащихся интерес к изучаемому материалу, их активность на протяжении всего урока. Игровые формы деятельности. Немаловажная роль, особенно в подростковом возрасте, отводится играм и игровым моментам на уроках математики – современному и признанному методу обучения и воспитания, обладающему образовательной, развивающей и воспитывающей функциями, которые действуют в органическом единстве. Игра – творчество, игра – труд. В процессе игры у детей вырабатывается привычка сосредоточиваться, мыслить самостоятельно, развивает внимание, стремление к знаниям. Увлекшись, дети не замечают, что учатся. Они познают, запоминают новое, ориентируются в необычных ситуациях, пополняют запас представлений, понятий, развивают фантазию. Даже самые пассивные из детей включаются в игру с огромным желанием, прилагая все усилия, чтобы не подвести товарищей по игре. Примером дидактической игры в 8 классе может служить игра « Математическое лото». Учащимся предлагается карточка с заданиями и карточки с ответами по теме «Система уравнений». Решив систему уравнений, предложенную на карточке и найдя сумму полученных корней , ученик находит ответ и кладет карточку с ответом лицевой стороной вверх на заданный пример. На карточке могут быть и неправильные ответы. На одной из сторон карточек приводится афоризм одного из философов или ученого- математика. В случае правильного ответа выстраивается целая фраза. Учитель, проходя по рядам может, легко отследить правильность выполнения заданий. Например, афоризм В.Гюго «Мышление-работа ума, мечтательность - его сладострастие» зашифрован в карточке: Результат:
Все педагогические средства могут стать реально действующими стимулами при условии, если ученик будет достигать успеха в познавательной деятельности. Таким образом, следует найти и закрепить те педагогические средства, которые действуют как положительные стимулы учения. Творческий подход к построению урока, его неповторимость, насыщенность многообразием приемов, методов и форм могут обеспечить его эффективность. Один из способов развития познавательной активности учащихся -применение наглядных методов обучения, среди которых необходимо выделить «видеометод». С помощью слайд-презентаций, видеофильмов, мультипликации можно повысить мотивацию обучения. Интенсивное проникновение в практику работы образовательных учреждений новых источников экранного преподавания информации позволяет рассматривать видеометод в качестве отдельного метода обучения. Видеометод служит не только для преподнесения знаний, но и для их контроля, закрепления, повторения, обобщения, систематизации. Обучающая и воспитывающая функции данного метода обусловливаются высокой эффективностью воздействия наглядных образов. Информация, представленная в наглядной форме, является наиболее доступной для восприятия, усваивается легче и быстрее. Рекомендации по развитию познавательного интереса на уроках математики На основании вышеизложенных фактов учителям в процессе обучения рекомендуется предусматривать такие пути, которые были бы обращены к различному уровню развития познавательного интереса учащихся и находили опору в различных сторонах обучения: в содержании, в организации процесса деятельности (самостоятельная работа), в приемах побуждения и активизации учащихся. Для этого необходимо в области обучения придавать большое значение глубокой и вдумчивой работе учителя по отбору содержания учебного материала, который составляет основу формирования научного кругозора учащихся, столь необходимого для появления и укрепления их познавательных интересов. А также: Знакомить учащихся с новыми фактами и сведениями, которые могут показать учащимся современный уровень науки и перспективы ее движения; Раскрывать перед ними интересующие вопросы: зарождение идеи, научные поиски, результаты открытий, трудности; При помощи проблемного обучения ставить учащихся перед противоречиями и учить диалектическому подходу в осмыслении научных фактов и идей; Показать необходимость научных выводов для объяснения явлений жизни, знаний, приобретенных личным опытом: Раскрывать перед учащимися практическую силу научных знаний, возможность применения приобретенных в школе знаний в жизни человека, на производстве, в сельском хозяйстве, при решении бытовых и практических вопросов. В организации процесса учения предлагается всемерно разнообразить самостоятельную работу учащихся, постоянно совершенствовать способы их познавательной деятельности: Постоянно усложнять познавательные задачи, по каждому предмету наметить систему усложненных задач, требующих овладения новыми, более совершенными познавательными умениями; Вводить задачи на догадку, развитие сообразительности, побуждая к различному подходу в их решении; Ставить задачи, требующие исследовательского подхода, проверки опытным путем полученных знаний; Практиковать задачи на применение знаний в жизни и быту; Развивать и поддерживать в самостоятельной работе творческое начало, требующее активности наблюдения, воображения, реконструкции опыта, самостоятельности мысли; Дифференцировать познавательные задачи для различных групп учащихся. Составлять несколько вариантов задач различной степени сложности, предлагать их свободный выбор. Отыскание важнейших путей побуждения учащихся к учению является необходимым условием развития их познавательных интересов. В этом плане рекомендуется : Оживлять уроки элементами занимательности, имея в виду решение поставленной на уроке задачи; Использовать всестороннее воздействие средств искусства; Побуждать учащихся задавать вопросы учителю, товарищам; Развивать на уроках коллективный анализ процесса и результатов работы отдельных учащихся; Практиковать индивидуальные задания, требующие знаний, выходящих за пределы программы; Использовать широкий кругозор отдельных учащихся в интересующей их области как дополнительный источник знаний для других; Рекомендовать дополнительную литературу. В области внеклассной работы предлагается: -Расширять и углублять кругозор учащихся в определенной, избранной ими области; -Практиковать решение научно – прикладных задач. Поставленные во внеклассной работе задачи могут быть решены самыми различными формами, поэтому рекомендуются те из них, которые получили достаточную апробацию в опыте школ: Вечера вопросов и ответов; Конкурсы смекалки; Диспуты; Вечера – зачетов, где раскрываются творческие возможности школьников; Исследования, опыты, наблюдения с определенным заданием или без него; Познавательные игры, игры – путешествия. В школе важно создать атмосферу интереса к знаниям, стремление искать, исследовать, творить, вносить техническую смекалку. Поэтому необходимо направлять педагогический коллектив на поиски самых разнообразных путей и приемов поддержания познавательных интересов учащихся в любом виде их деятельности, любом направлении: выдвигать наиболее актуальные для освещения вопросы перед учащимися через различные формы; вводить еженедельные обзоры об интересном в мире и в жизни; готовить выступления перед товарищами в классе; направлять деятельность учащихся на сбор интересного материала. Активизация познавательной деятельности ученика без развития его познавательного интереса не только трудна, но и практически невозможна. Вот почему в процессе обучения необходимо систематически развивать и укреплять познавательный интерес учащихся и как важный мотив учения, и как стойкую черту личности, и как мощное средство повышения качества обучения. |