Расчетная работа 1 ММвПИЭ. Расчетка1 Отчет. Получение математической модели по результатам однофакторного пассивного эксперимента
 Скачать 43.43 Kb. Скачать 43.43 Kb.
|
|
Министерство образования Республики Беларусь Учреждение образования БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ Факультет компьютерного проектирования Кафедра проектирования информационно-компьютерных систем Отчёт по расчётной работе №1 «ПОЛУЧЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ПО РЕЗУЛЬТАТАМ ОДНОФАКТОРНОГО ПАССИВНОГО ЭКСПЕРИМЕНТА» Выполнили: Проверила: студенты группы 910291 Сыс А.Д. Козел И.С. Кийко И.Н. Минск 2020 Цель работы: сгенерировать с помощью ЭВМ результаты опытов однофакторного пассивного эксперимента и, используя их, получить математическую модель объекта. Ход работы 7-й Вариант 1) При генерировании результатов эксперимента приняты следующие обозначения: x – параметр, влияющий на выходную характеристику объекта (ЭУ), рассматривается в качестве фактора; y – выходной параметр ЭУ, рассматривается в качестве функции отклика; n – число пар значений x и y, при выполнении задания принимается n = 16. Результаты однофакторного эксперимента приведены в таблице 1. Таблица 1 – Результаты однофакторного эксперимента
2) На прямоугольную координатную сетку наносим точки с координатами (x1, y1), (x2, y2), …, (xn, yn) для получения диаграммы разброса (корреляционного поля) параметров х и y (рис. 1). 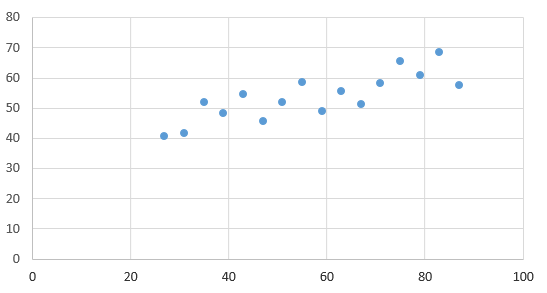 Рисунок 1– Диаграмма разброса параметров x и y 3) Об удачности линейного уравнения регрессии можно судить также по значению коэффициента детерминации R2, определяемому по выражению: 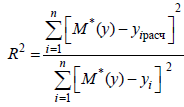 . .Подсчитанное значение M*(y) = 53,7 Значения yiи yрасч1 iприведены в таблице 1. По вышеуказанной формуле находим коэффициент детерминации R2 = 1. Подсчитанный вручную коэффициент совпал с рассчитанным инструментов Регрессия (рис. 2).  Рисунок 2 – Полученные результаты инструмента Регрессия Справедливо неравенство 0 ≤ R2 ≤ 1. Коэффициент детерминации R2 показывает, какая доля вариации отклика y объясняется изменениями фактора x. Чем ближе R2 к единице, тем лучше линейная функция y = ax + b описывает поведение отклика y. В нашем опыте R2 = 1, то есть модель объясняет наблюдаемые изменения y на 100%. 4) Информация об апробированных функциях, используемых в качестве математических моделей РЭУ представлена в таблице 3. Информация должна включать запись математического вида моделей, значения коэффициентов моделей и их статистическую значимость. Таблица 3 – Информация о моделях
Вывод: Пользуясь сгенерированными результатами опытов однофакторного эксперимента были получены линейная, показательная и степенная математическая модель объекта. Далее с помощью F-статистики Фишера был сделан вывод о том, что найденные математические модели статистически значимы (Fрасч1 = 27,43> 4,6; Fрасч2 = 8,71*1032> 4,6;Fрасч3 = 553,71 > 4,6). Следующим шагом была проверка статистической значимости коэффициентов a и b с помощью t-критерия Стьюдента, а также по значению уровня значимости (P-значение). В первой модели оба коэффициента оказались значимыми (|tрасч1 a| = 6,82 > 2,14, |tрасч1 b| = 13,37 > 2,14). Во второй модели оба коэффициента оказались значимыми (|tрасч2 a| = 6,94 > 2,14, |tрасч2 b| = 70,99 > 2,14). В третьей модели оба коэффициента оказались значимыми (|tрасч3 a| = 0,9*1016 > 2,14, |tрасч3 b| = 3,8*1015 > 2,14). По найденному значению коэффициента детерминации R2 сделан вывод о том, что линейная модель объясняет наблюдаемые изменения y на 99,33%. Также была подсчитана относительная ошибка Δср, значение которой у линейной составило 0,67%, у показательной 7,1%, степенной 9,1%. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

