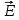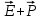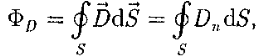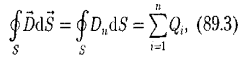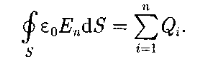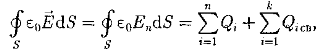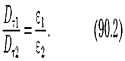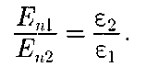сила лоренца. Поляризация диэлектриков. Поляризованность. Поляризационные заряды. Теорема Гаусса для диэлектриков. Электрическое смещение. Граничные условия
 Скачать 94.92 Kb. Скачать 94.92 Kb.
|
|
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПО ЗЕМЛЕУСТРОЙСТВУ» Факультет Городской кадастр Кафедра высшей математики и физики Реферат №1 на тему: Поляризация диэлектриков. Поляризованность. Поляризационные заряды. Теорема Гаусса для диэлектриков. Электрическое смещение. Граничные условия. Студентка: _______ Балуева Татьяна Алексеевна Группа: 11ПГ Преподаватель: __________ доцент Зубов Д. В. Москва 2022 Содержание
Введение Суть явления поляризации заключается в том, что под воздействием внешнего электрического поля связанные заряды диэлектрика смещаются в направлении действующих на них сил и тем больше, чем выше напряжённость поля. Своё применение в электротехнических приборах диэлектрики нашли за счёт способности поляризоваться. Диэлектриком называют "вещество, основным электрическим свойством которого является способность поляризоваться в электрическом поле" и в котором возможно существование электростатического поля, так как электрические заряды его атомов, молекул или ионов связаны . Используемые же на практике диэлектрики содержат и свободные заряды, которые, перемещаясь в электрическом поле, обуславливают электропроводность на постоянном токе. По современным представлениям, электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создаёт в окружающем пространстве электрическое поле, которое оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела. Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции. Глава 1. Поляризация диэлектриков Поляризацией диэлектрика называется процесс ориентации диполей или появления под воздействием внешнего электрического поля ориентированных по полю диполей. Соответственно трём группам диэлектриков различают три вида поляризации: Электронная, или деформационная, поляризация диэлектрика с неполярными молекулами, заключающаяся в возникновении у атомов индуцированного дипольюго момента за счёт деформации электронных орбит; Ориентационная, или дипольная, поляризация диэлектрика с полярными молекулами, заключающаяся в ориентации имеющихся дипольных моментов молекул по полю. Естественно, что тепловое движение препятствует полной ориентации молекул, но в результате совместного действия обоих факторов (электрическое поле и тепловое движение) возникает преимущественная ориентация дипольных моментов молекул по полю. Эта ориентация тем сильнее, чем больше напряжённость электрического поля и ниже температура; Ионная поляризация диэлектриков с ионными кристаллическими решётками, заключающаяся в смещении подрешетки положительных ионов вдоль поля, а отрицательных — против поля, приводящем к возникновению дипольных моментов. [1] Глава 2. Поляризованность. Поляризационные заряды При помещении диэлектрика во внешнее электрическое поле он поляризуется, т.е. приобретает отличный от нуля дипольный момент 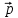 V =∑ V =∑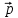 i , где pi — дипольный момент i-й молекулы. i , где pi — дипольный момент i-й молекулы.Для количественного описания поляризации диэлектрика пользуются векторной величиной — поляризованностью, определяемой как дипольный момент единицы объема диэлектрика:
Из опыта следует, что для большого класса диэлектриков (за исключением сегнетоэлектриков) поляризованность Р линейно зависит от напряженности поля Ё. Если диэлектрик изотропный и Ё не слишком велико, то
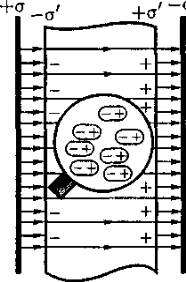
где ае — диэлектрическая восприимчивость вещества, характеризующая свойства диэлектрика; ае — величина безразмерная, причем всегда ае > 0 и для большинства диэлектриков (твердых и жидких) составляет несколько единиц (хотя, например, для спирта за ≈ 25, для воды ае = 80). Для установления количественных закономерностей поля в диэлектрике внесем в однородное внешнее электрическое поле 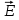 0 (создается двумя бесконечными параллельными разноименно заряженными плоскостями) пластинку из однородного диэлектрика, расположив ее так, как показано на рис. 1. 0 (создается двумя бесконечными параллельными разноименно заряженными плоскостями) пластинку из однородного диэлектрика, расположив ее так, как показано на рис. 1.Под действием поля диэлектрик поляризуется, т. е. происходит смещение зарядов: положительные смещаются по полю, отрицательные — против поля. [1] В результате этого на правой грани диэлектрика, обращенного к отрицательной плоскости, будет избыток положительного заряда с поверхностной плотностью +σ', на левой — отрицательного заряда с поверхностной плотностью —а'. Эти некомпенсированные заряды, появляющиеся в результате поляризации диэлектрика, называются связанными.
Поверхностная плотность σ' меньше плотности а свободных зарядов плоскостей, поэтому не все поле Ё компенсируется полем зарядов диэлектрика: часть линий напряженности пройдет сквозь диэлектрик, другая же часть обрывается на связанных зарядах. Следовательно, поляризация диэлектрика вызывает уменьшение в нем поля по сравнению с первоначальным внешним полем. Вне диэлектрика Е — Ео. Таким образом, появление связанных зарядов приводит к возникновению дополнительного электрического поля Е' (поля, создаваемого связанными зарядами), которое направлено против внешнего поля E0(поля, создаваемого свободными зарядами) и ослабляет его. Результирующее поле внутри диэлектрика
Поле [поле, созданное двумя бесконечными заряженными плоскостями;], поэтому
Определим поверхностную плотность связанных зарядов σ’. По (1) полный дипольный момент пластинки диэлектрика pv = PV = PSd, где S —площадь грани пластинки, d — ее толщина. [1] С другой стороны, полный дипольный момент, равен произведению связанного заряда каждой грани Q' — σ’S нa расстояние d между ними, т.е. рV= σ’Sd или σ’=P
т.е. поверхностная плотность σ связанных зарядов равна поляризованности Р. Подставив в (4) выражения (5) и (2), получаем Е= E0- aeЕ, откуда напряженность результирующего поля внутри диэлектрика равна
Безразмерная величина Ε=1+ae (7) называется диэлектрической проницаемостью среды. Сравнивая (6) и(7), видим, что ε показывает, восколько раз поле ослабляется диэлектриком, и характеризует количественносвойство диэлектрика поляризоватьсяв электрическом поле. [1] Глава 3. Теорема Гаусса для диэлектриков. Электрическое смещение Напряженность электростатического поля, согласно (6), зависит от свойств среды: в однородной изотропной среде напряженность поля Е обратно пропорциональна ε. Вектор напряженности Ё, переходя через границу диэлектриков, претерпевает скачкообразное изменение, создавая тем самым неудобства при расчетах электростатических полей. Поэтому оказалось необходимым помимо вектора напряженности характеризовать поле еще вектором электрического смещения, который для электрически изотропной среды, по определению,
Используя формулы (7) и (2), вектор электрического смещения можно выразить как
Единица электрического смещения —кулон на метр в квадрате (Кл/м2). Рассмотрим, с чем можно связать вектор электрического смещения. Связанные заряды появляются в диэлектрике при наличии внешнего электростатического поля, создаваемого системой свободных электрических зарядов, т. е. в диэлектрике на электростатическое поле свободных зарядов накладывается дополнительное поле связанных зарядов. Результирующее поле в диэлектрике описывается вектором напряженности Е, и потому он зависит от свойств диэлектрика. Вектором D описывается электростатическое поле, создаваемое свободными зарядами. Связанные заряды, возникающие в диэлектрике, могут вызвать, однако, перераспределение свободных зарядов, создающих поле. Поэтому вектор D характеризует электростатическое поле, создаваемое свободными зарядами (т.е. в вакууме), но при таком их распределении в пространстве, какое имеется при наличии диэлектрика. [1] Аналогично, как и поле Ё, поле D изображается с помощью линий электрического смещения,направление игустота которых определяются точно так же, как и для линий напряженности. Линии вектора Ё могут начинаться и заканчиваться на любых зарядах — свободных и связанных, в то время как линии вектора D — только на свободных зарядах.Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь. Для произвольной замкнутой поверхности S поток вектора D сквозь этуповерхность
где Dn — проекция вектора D на нормаль п к площадке dS. Теорема Гаусса для электростатического поля в диэлектрике:
т.е. поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов. В такой форме теорема Гаусса справедлива для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред. Для вакуума Dn = ε0Еп (ε=1), тогда поток вектора напряженности Е сквозь произвольную замкнутую поверхность равен
Так как источниками поля Ё в среде являются как свободные, так и связанные заряды, то теорему Гаусса для поля Ё в самом общем виде можно записать как
Где Глава 4. Граничные условия Рассмотрим связь между векторами Ё и D на границе раздела двух однородных изотропных диэлектриков (диэлектрические проницаемости которых ε1и ε2) при отсутствии на границе свободных зарядов. Построим вблизи границы раздела диэлектриков 1 и 2 небольшой замкнутый прямоугольный контур ABCDA длиной l, ориентировав его так, как показано на рис. 2. Согласно теореме о циркуляции вектора Е, 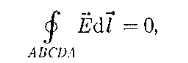 откуда (знаки интегралов по АВ и СDразные, так как пути интегрирования противоположны, а интегралы по участкам ВС и DAничтожно малы). Поэтому
Заменив, согласно (8), проекции вектора Ё проекциями вектора D, деленными на ε0ε, получим
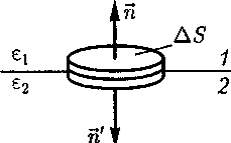
На границе раздела двух диэлектриков (рис. 3) построим прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом диэлектрике, другое — во втором. Основания ΔS настолько малы, что в пределах каждого из них вектор Dодинаков. Согласно теореме Гаусса (11), Dµ1ΔS- Dµ2ΔS=0 (нормали п и п' к основаниям цилиндра направлены противоположно). Поэтому
Заменив, согласно (8), проекции вектора D проекциями вектора Е, умноженными на ε0ε, получим
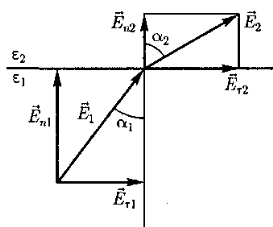
Таким образом, при переходе через границу раздела двух диэлектрических сред тангенциальная составляющая вектора  (Еτ)и нормальная составляющая вектора D(Dn)изменяются непрерывно (не претерпевают скачка), а нормальная состав-ляющая вектора (Еτ)и нормальная составляющая вектора D(Dn)изменяются непрерывно (не претерпевают скачка), а нормальная состав-ляющая вектора  (Еn) и тангенциальная составляющая вектора D(Dτ)претерпевают скачок. [1] (Еn) и тангенциальная составляющая вектора D(Dτ)претерпевают скачок. [1]Из условий (14)—(17) для составляющих векторов 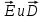 следует, что линии этих векторов испытывают излом (преломляются). Найдем связь между углами α1 и α2 (на рис. 4 ε2>ε1). Согласно (14) и (17), Eτ1=Eτ2 и ε2En2= ε1En1 следует, что линии этих векторов испытывают излом (преломляются). Найдем связь между углами α1 и α2 (на рис. 4 ε2>ε1). Согласно (14) и (17), Eτ1=Eτ2 и ε2En2= ε1En1Разложим векторы Е1 и Е2у границы раздела на тангенциальные и нормальные составляющие. Из рис. 4 следует 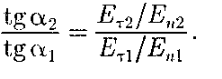
Учитывая записанные выше условия, получим закон преломления линий напряженности Е (а значит, и линий смещения D) 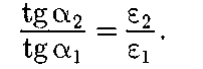 Эта формула показывает, что, входя в диэлектрик с большей диэлектрической проницаемостью, линии Е и D удаляются от нормали. [1] Заключение Электрическое поле — особая форма поля, существующая вокруг тел или частиц, обладающих электрическим зарядом, а также в свободном виде в электромагнитных волнах. Электрическое поле непосредственно невидимо, но может наблюдаться по его действию и с помощью приборов. Основным действием электрического поля является ускорение тел или частиц, обладающих электрическим зарядом. Электрическое поле можно рассматривать как математическую модель, описывающую значение величины напряженности электрического поля в данной точке пространства. Электрическое поле является одной из составляющих единого электромагнитного поля и проявлением электромагнитного взаимодействия. Список литературы Курс физики: учеб. пособие для вузов / Таисия Ивановна Трофимова. — 11-е изд., стер. — М.: Издательский центр «Академия», 2006. — 560 с. (дата обращения 01.03.2022 г.) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

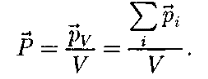
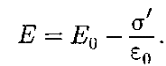
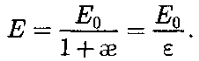
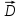 =ε0ε
=ε0ε