ПономаревСеместровая. Пономарев Н. Д п220
 Скачать 3.69 Mb. Скачать 3.69 Mb.
|
|
Вариант 64 Пономарев Н.Д П-220 100 сверл были подвергнуты испытанию на твердость. При этом фиксировалась твердость лапки. Результаты испытания представлены следующим рядом значений:
Упорядочим выборку, т.е. запишите все значения 𝑥 случайной величины 𝑋 в возрастающем порядке. Если какое-либо значение повторяется, запишем его столько раз, сколько оно встретилось.
Для построения интервального ряда определим интервальный шаг выборки, воспользовавшись формулой Стерджеса 𝑘 = 1 + 3,322 ∙ lg 𝑛, где n – объем выборки (в нашем случае 100). 𝑘 = 1 + 3,322 ∙ lg 100 ≈ 1 + 3,322 ∙ 1,857 ≈ 8 Ширину каждого интервала берем одинаковой и равной ℎ = (𝑥𝑚𝑎𝑥 – 𝑥𝑚𝑖𝑛)/𝑘 . Величину ℎ выбираем с точностью выборки и округляем в сторону завышения. ℎ=(11,29-6,85)/8=0,56. Границы интервалов вычисляем по формуле 𝑥1 = 𝑥𝑚𝑖𝑛, 𝑥𝑖+1 = 𝑥𝑖 + ℎ (𝑖 = 1,2, … , 𝑘). За начало первого интервала примем 𝑥1 = 𝑥𝑚𝑖𝑛 =6,85 Подсчитываем 𝑛𝑖 − количество элементов 𝑥𝑖 , попавших в i-й интервал (частота интервала). Если элемент совпадает с границей интервала, то он относится к предыдущему интервалу. Вычисляем относительные частоты интервалов по формулам 𝑤𝑖 = 𝑛𝑖 𝑛 (𝑖 = 1,2, … 𝑘) 𝑥̃𝑖 = (𝑥𝑖−1 + 𝑥𝑖)/2.
Модой Mo вариационного ряда называется варианта, которая имеет наибольшую частоту: 𝑀𝑜 =8.81 Медианой Me вариационного ряда называется значение признака, приходящееся на середину ранжированного ряда наблюдений. Медиану можно найти, также воспользовавшись формулой: если количество вариант 𝑥𝑖 в дискретном вариационном ряду 𝑛 = 2𝑘 + 1 (нечетное число), то 𝑀𝑒 = 𝑥𝑘+1; если 𝑛 = 2𝑘 (четное число), то 𝑀𝑒 = 𝑥𝑘+1+𝑥𝑘 2. Таким образом, так как количество вариант 𝑥𝑖 в нашем примере 𝑛 = 8 – четной число, то 2k = 8, тогда 𝑘 = 4, отсюда 𝑀𝑒 = 𝑥𝑘 = 𝑥4 = 8,81. Выборочной средней 𝑥̅В называют среднее арифметическое значение признака выборочной совокупности: 𝑥̅В = 1/𝑛∑𝑥𝑖 ∙ 𝑛𝑖=898,36/100=8,9836 Выборочная дисперсия 𝐷В равна: 𝐷В = 1/𝑛∑(𝑥𝑖 − 𝑥̅В )^2 ∙ 𝑛𝑖= 1/𝑛∑𝑥𝑖^2 ∙ 𝑛𝑖− 𝑥̅В^2 = 8166,9044/100-8,9836^2=0.9639. Среднее квадратическое отклонение равно Ơ=√𝐷В=0.9818. Коэффициент вариации 𝑉 = 𝜎/𝑥̅В ∙ 100 = 0.9818/8,9836∙ 100 = 10.9(%) 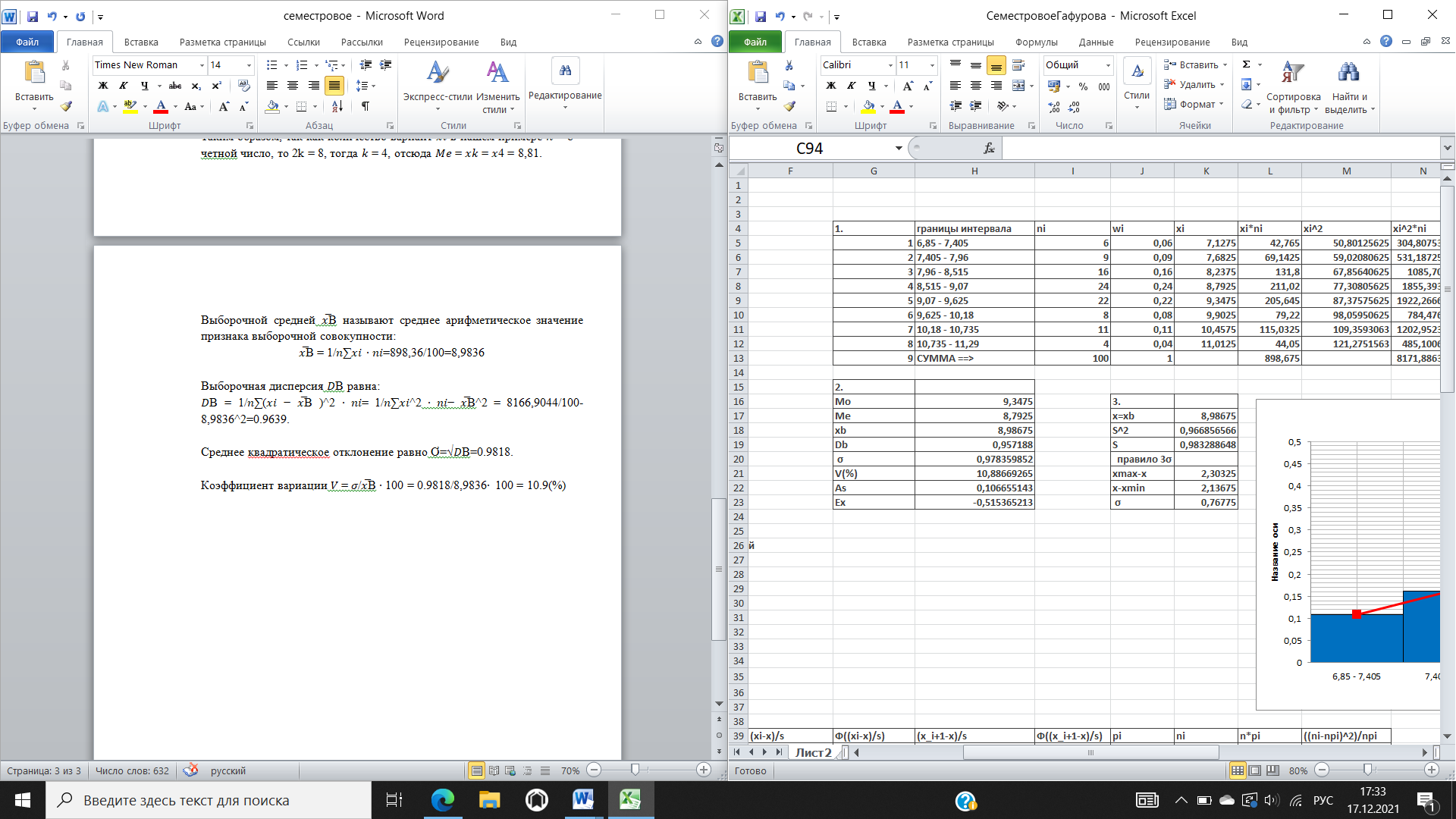 Отрицательный эксцесс указывает на относительно пологое распределение. Несмещенные оценки 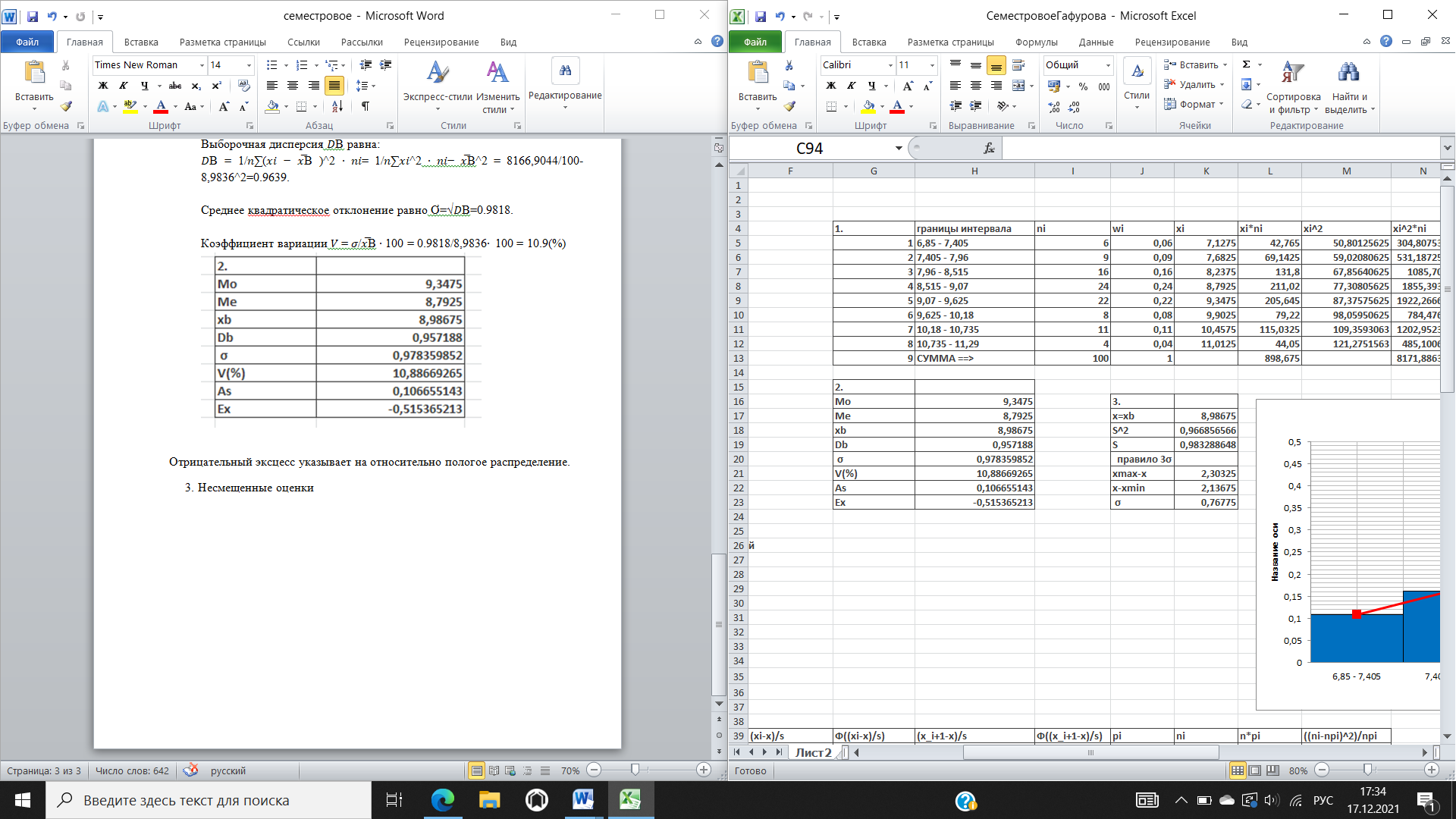 Для сравнения подсчитаем 𝜎̅ по «правилу 𝟑𝜎». Так как для случайной величины, имеющей нормальное распределение, почти все рассеивания укладывается на участке 𝟑𝜎, то с помощью «правила 𝟑𝜎» можно ориентировочно определить оценку среднего квадратичного отклонения случайной величины. Берем максимальное практически возможное отклонение от среднего значения и делим его на три. Гистограмма – это ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной ℎ, а высоты равны 𝑤𝑖⁄ℎ (плотность относительной частоты). 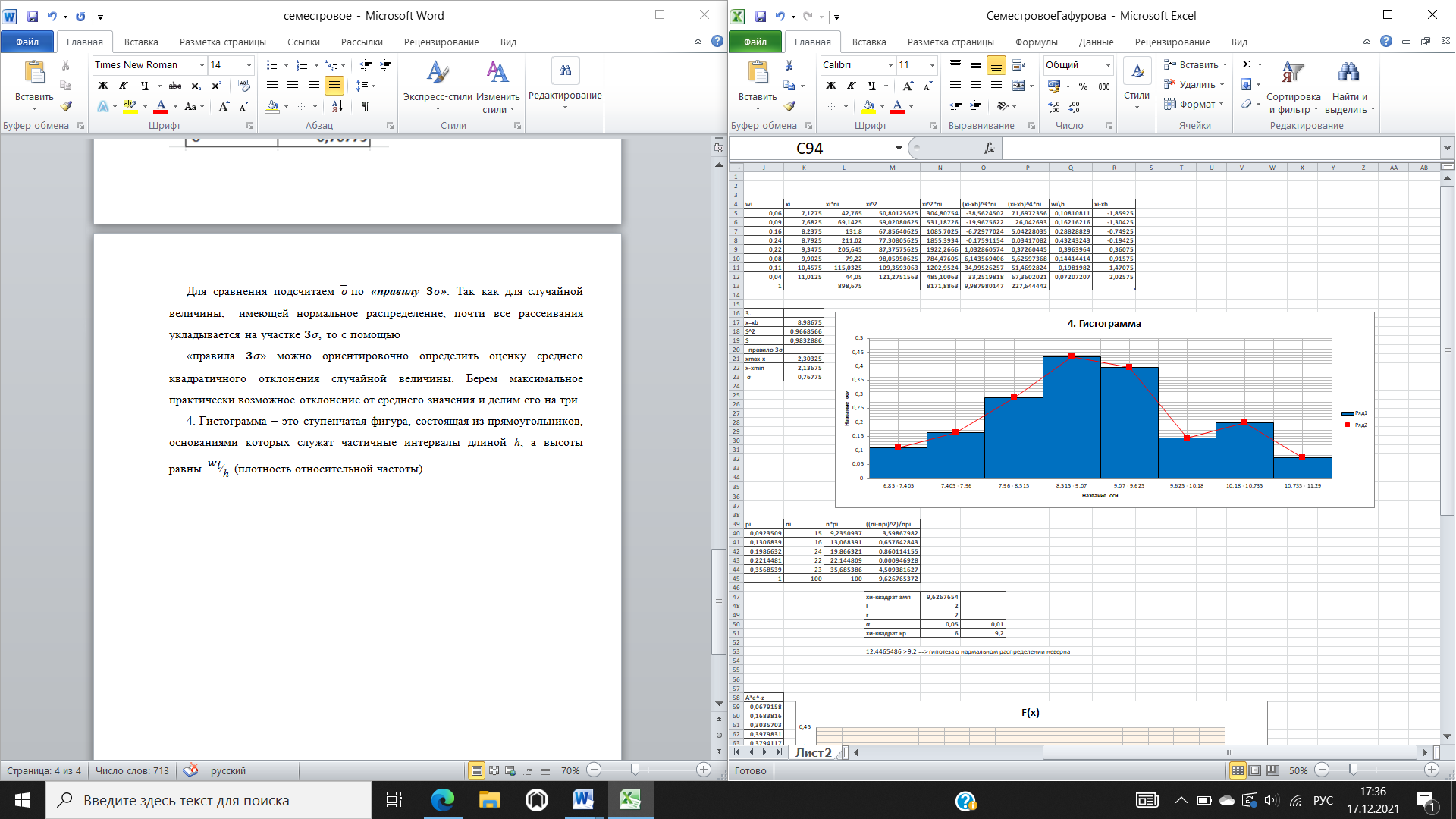 По данным таблицы построим точки с координатами (𝑥̃𝑖, 𝑤𝑖⁄ℎ) и соединим их плавной пунктирной линией. Эта линия будет аналогом плотности распределения случайной величины и, следовательно, по виду гистограммы можно выдвинуть гипотезу о нормальном распределении (или о распределении, близком к нормальному) случайной величины с плотностью. Выполним предварительный выбор закона распределения случайной величины. Предварительный закон распределения может определяться по величине коэффициента вариации наблюденных данных. Если коэффициент вариации попадает в интервал [0,01; 0,40], то можно выдвинуть гипотезу о нормальном законе распределения; если в интервал [0,6;1,3], то можно выдвинуть гипотезу об экспоненциальном законе распределения. В нашем распределении коэффициент вариации V= 10.9% = 0,109 попадает в первый интервал, поэтому выдвигаем гипотезу о нормальном законе распределения. Следующим критерием оценки гипотезы в случае нормального закона распределения является то, что асимметрия и эксцесс близки к нулю, в нашем примере As = 0,1066 и Ex = -0,515, что достаточно близко к нулю. Также гипотеза о нормальном законе распределения может быть принята, если выполняются неравенства: |𝐴𝑠| < 3 ∙ 𝐸𝐴 и |𝐸𝑥| < 3 ∙ 𝐸𝐸, где 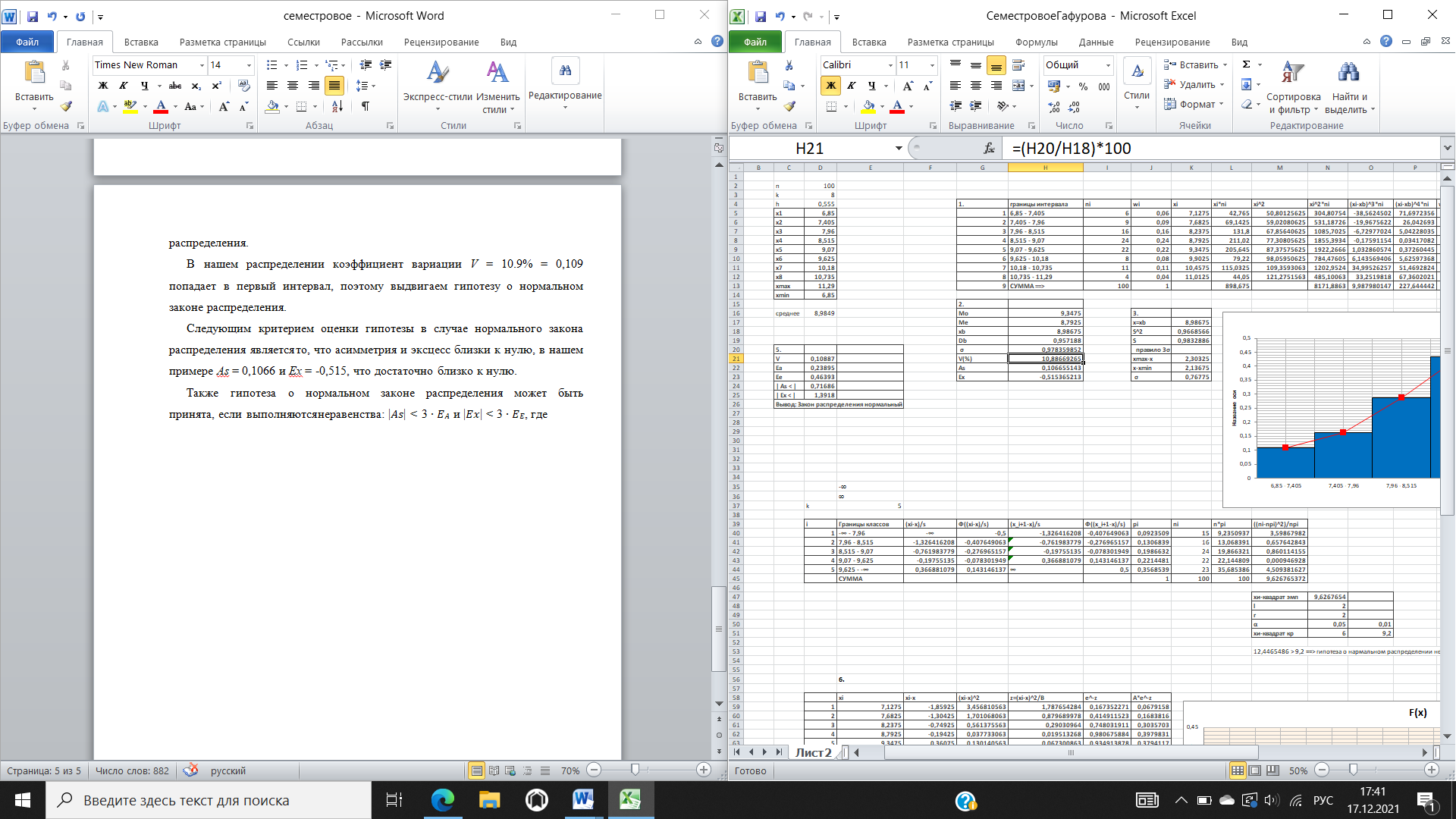 Таким образом, |𝐴𝑠| < 0,71686 и |𝐸𝑥| < 1,3918 Сделаем вывод: основываясь на значениях коэффициентов вариации (находится в интервале [0,01; 0,40]), асимметрии (близок к нулю), эксцесса (близок к нулю и выполнении неравенств, можно предположить, что признак подчинен нормальному закону распределения. Для строгой проверки гипотезы о нормальном распределении признака применим критерии согласия. Они позволяют ответить на вопрос являются ли неизбежные расхождения между эмпирическим и теоретическим распределениями случайными или теоретический закон подобран неудачно. χ2 – Пирсона. При его использовании сравниваются эмпирические 𝑛𝑖 теоретические (предполагаемые) 𝑛𝑖′частоты. Для проверки гипотезы о нормальном распределении рассматриваемой величины заполним таблицу .
Для проверки гипотезы о нормальном распределении случайной величины в качестве меры расхождения между теоретическим и статистическим распределениями выберем случайную величину. 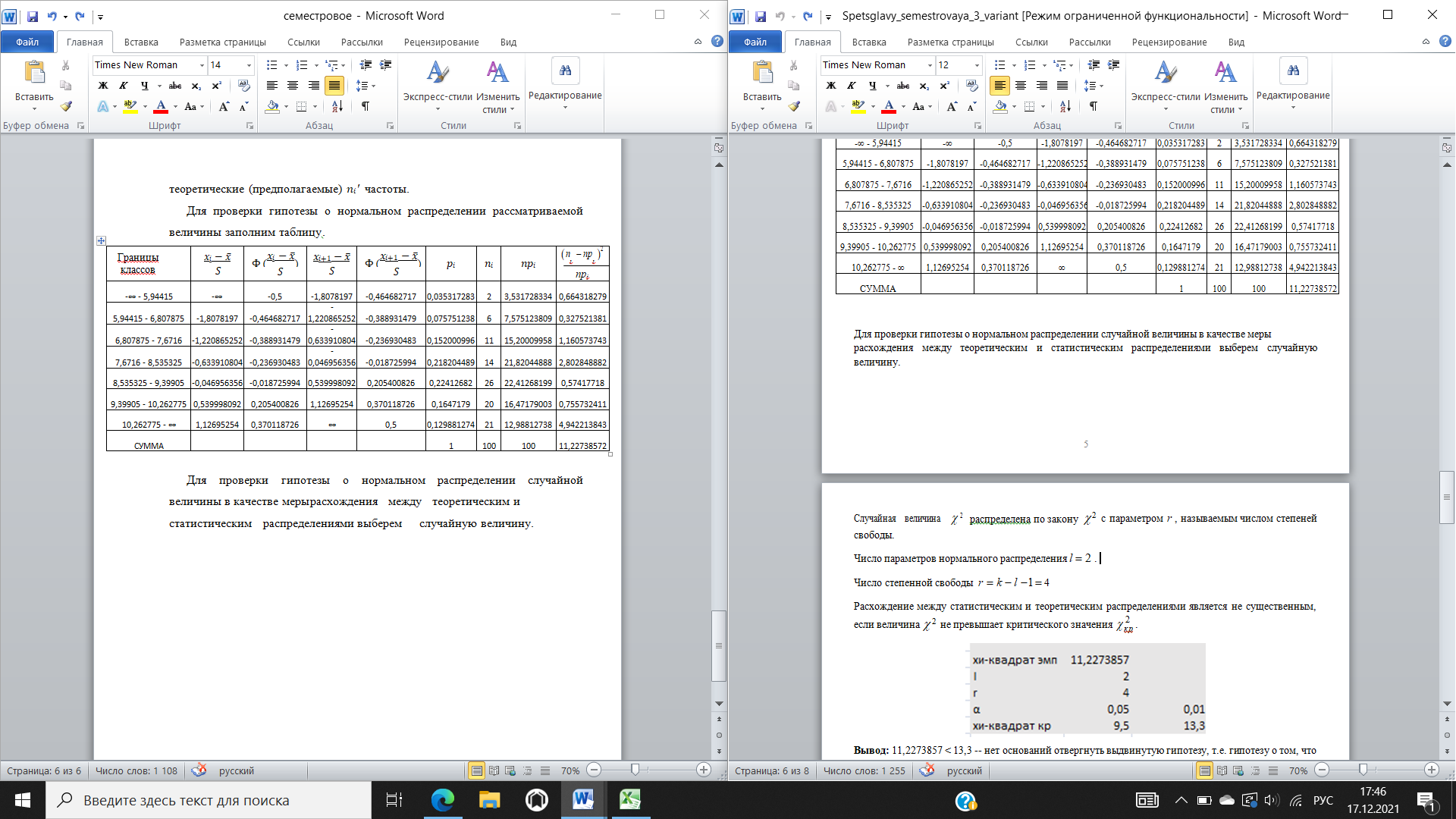 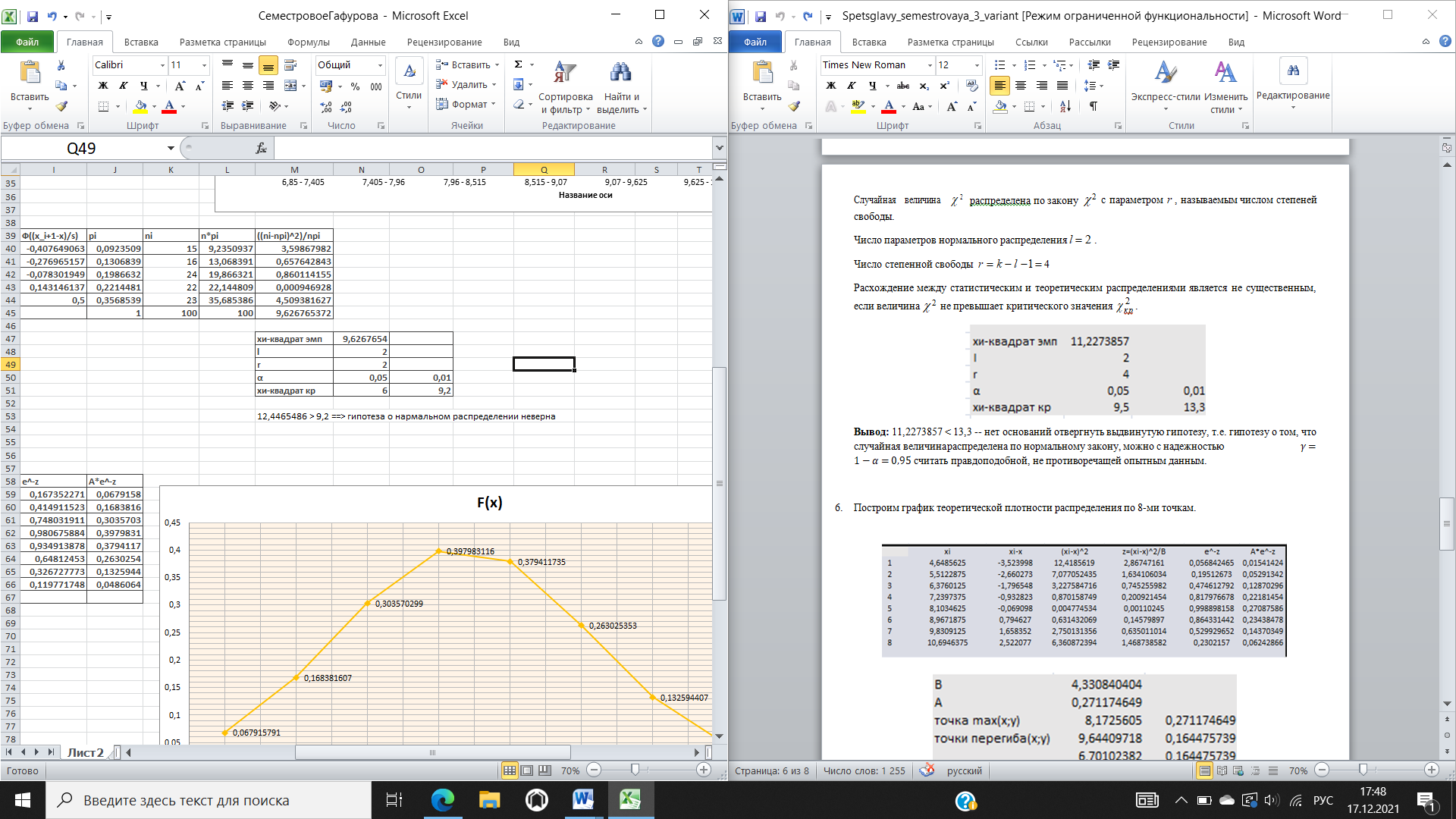 Вывод: 9,6267654 < 13,3 -- нет оснований отвергнуть выдвинутую гипотезу, т.е. гипотезу о том, что случайная величина распределена по нормальному закону, можно с надежностью 𝛾 = 1 − 𝛼 = 0,95 считать правдоподобной, не противоречащей опытным данным. Построим график теоретической плотности распределения по 8-ми точкам. 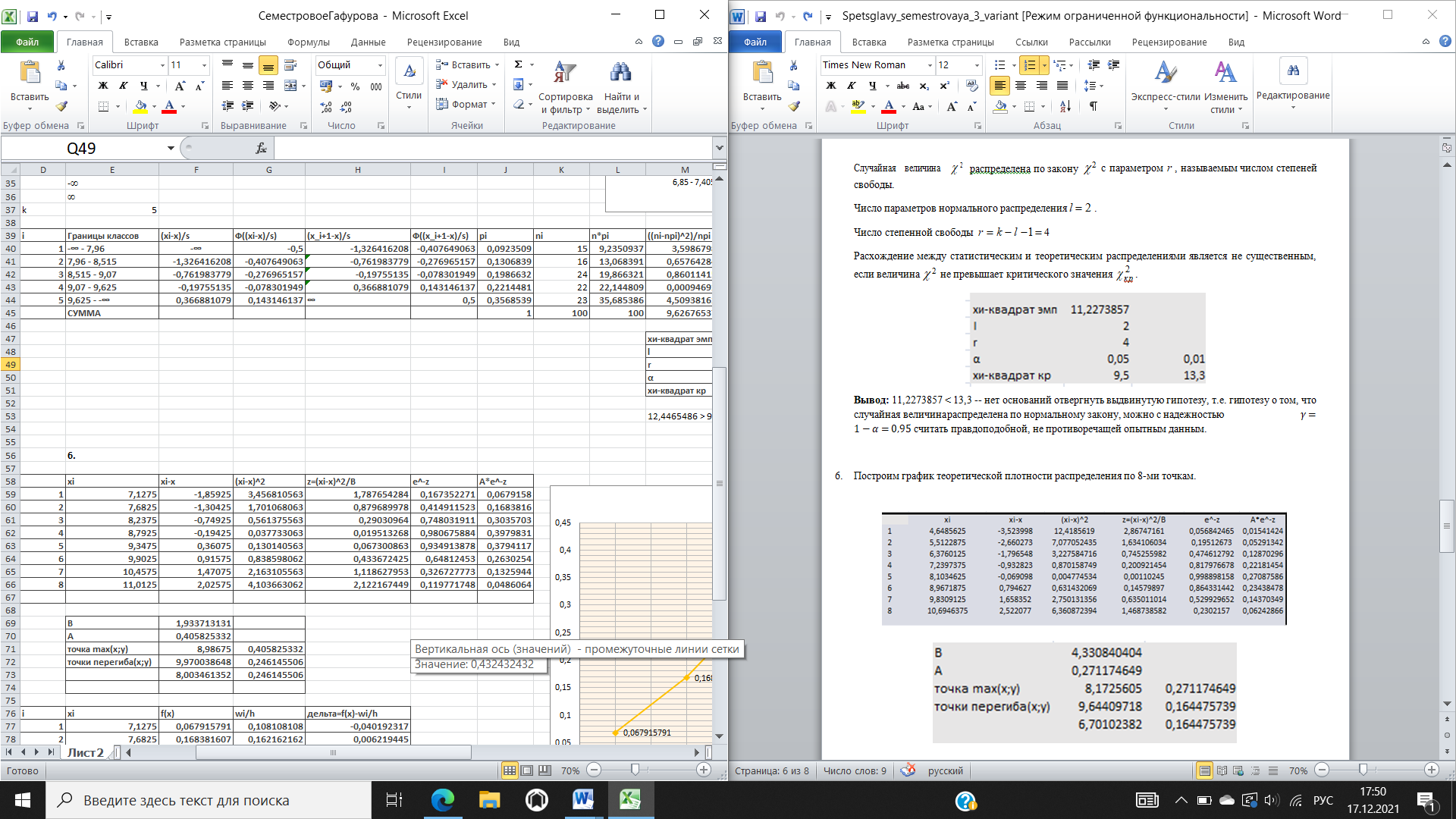   Отклонение не большое = закон распределения выбран правильно 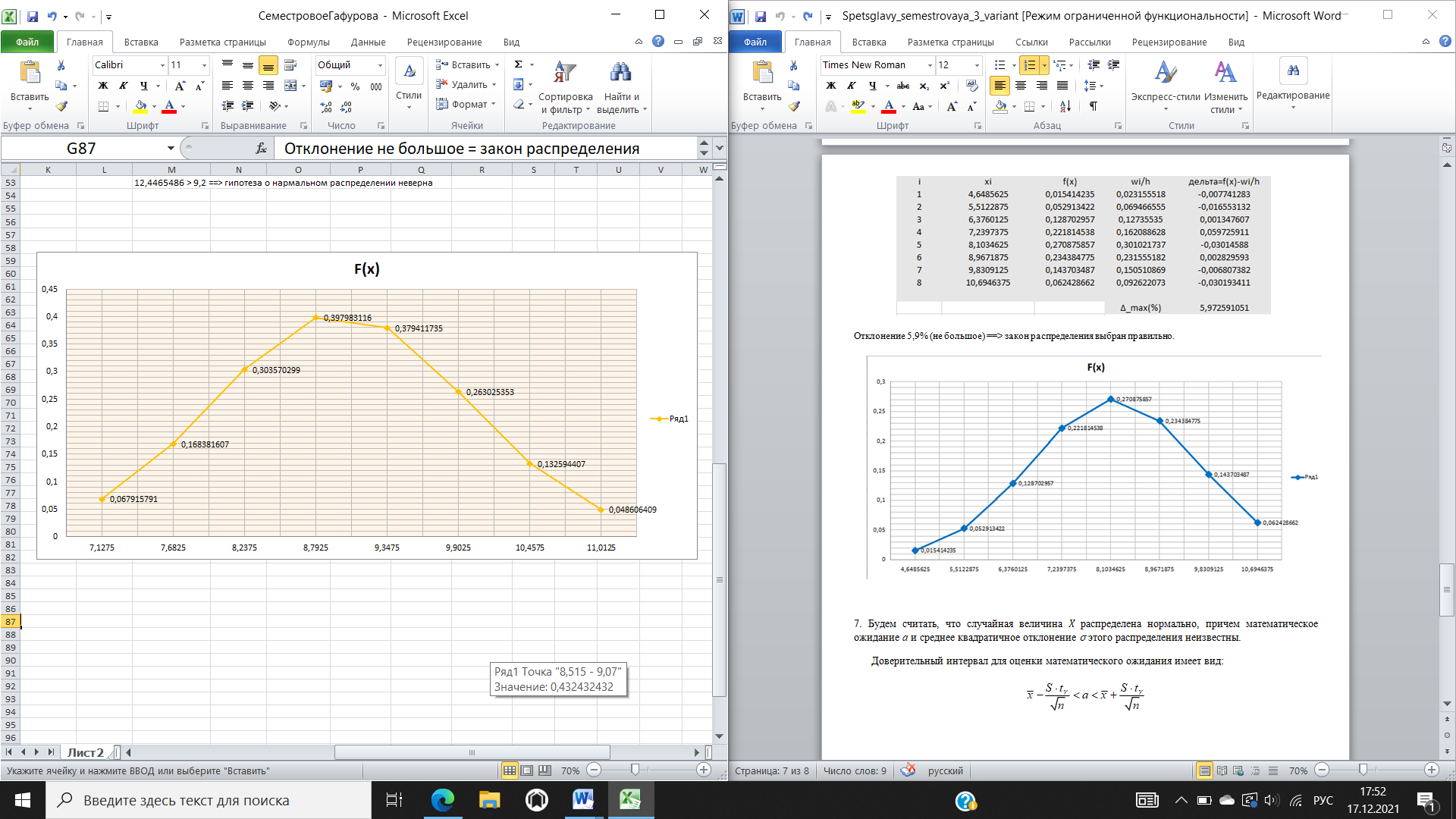 Будем считать, что случайная величина 𝑋 распределена нормально, причем математическое ожидание аи среднее квадратичное отклонение этого распределения неизвестны. Доверительный интервал для оценки математического ожидания имеет вид: 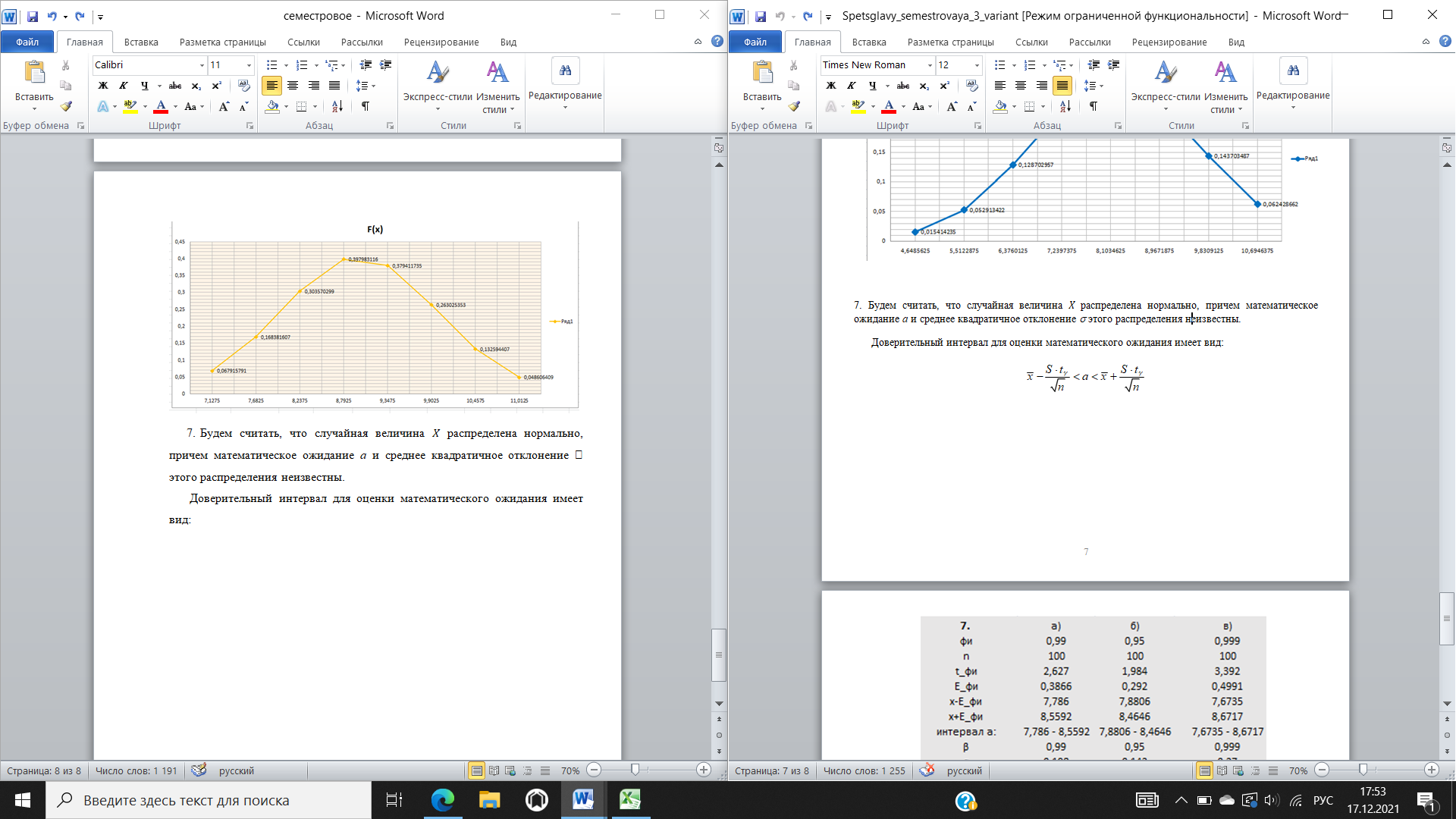 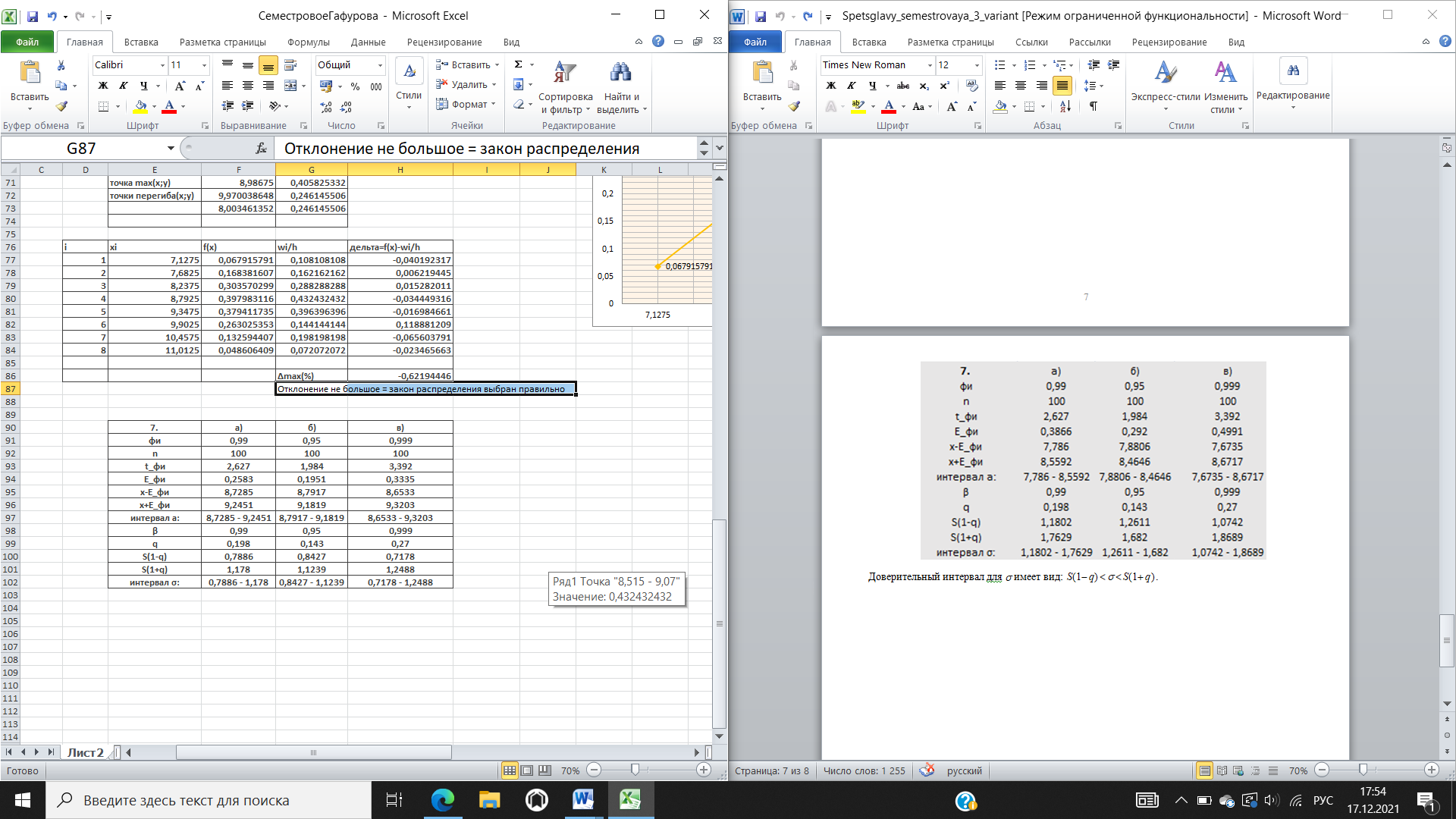 Доверительный интервал для имеет вид: S(1 q) S(1 q). |
