ИГА. Понятие базы данных
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
Хеширование данных.Хеш-таблицей называется структура данных, предназначенная для реализации ассоциативного массива, такого в котором адресация реализуется посредством хеш-функции. Хеш-функция – это функция, преобразующая ключ key в некоторый индекс iравныйh(key), где h(key) – хеш-код (хеш-сумма, хеш) key. Весь процесс получения индексов хеш-таблицы называется хешированием. В общем случае хеш-таблица позволяет организовать массив, специфика которого проявляется в связанности индексов по отношению к хеш-функции; индексы могут быть не только целого типа данных (как это было в простых массивах), но и любого другого, для которого вычислимы хеш-коды. Данные, хранящиеся в виде такой структуры, удобны в обработке: хеш-таблица позволяет за минимальное время (O(1)) выполнять операции поиска, вставки и удаления элементов. Предположим, имеется товарная накладная с информацией о датах и городах (когда и куда отправляются товары). Определенному товару соответствует его числовой код в диапазоне от 000000000 до 999999999:
Здесь ключами являются коды товаров, и как видно они, несмотря на отсутствие некоторых единиц продукции, заполняют весь диапазон. Такая организация данных не оптимальна, поскольку памяти для хранения списка выделяется больше чем нужно. Решением проблемы будет хеширование ключей списка. И хорошо если известно у скольких элементов значения отсутствуют, тогда в качестве ключей можно использовать все те же коды, но когда это не так, то лучше в качестве них взять другие данные, например (в накладной) ими могут быть даты. У девятизначных кодов ключи имеют целочисленный тип данных, а у дат – символьные (строковые). Для хеширования понадобиться хеш-функция. В качестве последней можно взять, например следующую: string hashf(string key) {string h=key.erase(0, 5); return (h);} Например, из ключа 2026-09-01, путем хеширования, получился хеш-код 09-01. Таким образом, размер накладной заметно сокращается, исчезают все пустые элементы. Но в некоторых местах возможно возникновения проблем следующего типа: пусть имеется два ключа: 2017-06-06 и 2025-06-06, тогда результат работы функции в двух случаях будет 06-06, следовательно, разные значения в хеш-таблицы попадут под один и тот же индекс. Такая ситуация называется коллизией. Коллизий следует избегать, выбирая «хорошую» хеш-функцию, Хорошая хеш-функция должна удовлетворять двум свойствам: Быстро вычисляться; Минимизировать количество коллизий и используя один из методов разрешения конфликтов: открытое (метод цепочек) или закрытое (открытая адресация) Открытое хеширование (Метод цепочек) Принцип организации хеш-таблицы методом открытого хеширования заключается в реализации логически связанных цепочек, начинающихся в ячейках хеш-таблицы. Под цепочками подразумеваются связанные списки, указатели на которые хранятся в ячейках хеш-таблицы. Каждый элемент связанного списка – блок данных, и если с некоторым указателем, хранящимся по адресу i, связаны n таких блоков (n>1), то это свидетельствует о том, что n ключей получили один и тот же хеш-код i, т. е. имеет место коллизия. Но метод открытого хеширования устраняет конфликт, поскольку данные хранятся не в самой таблице, а в связных списках, которые увеличиваются при возникновении конфликта. 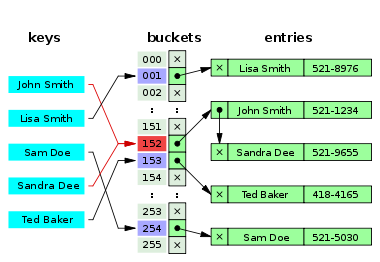  На рисунке изображены связанные списки со ссылающейся на них хеш-таблицей (ее размер = M). Первый столбец таблицы содержит хешированные значения ключей, второй – ссылки на списки. Количество последних ограничено лишь числом элементов исходного массива (он не показан, но предполагается). Состоят списки из трех (последний элемент подсписка – из двух) полей: & — адрес элемента списка, $ — данные, * — указатель (ссылка). Если в исходном массиве было всего N элементов (столько же будут содержать в совокупности и все списки), то средняя длина списков будет равна α=N/M, где M – число элементов хеш-таблицы, α – коэффициент заполнения хеш-таблицы. Предположив, например, что в списке на рисунке выше M=5 (заклеив 4-ую по счету строку), получим среднее число списков α=2. Чтобы увеличить скорость работы операций поиска, вставки и удаления нужно, зная N, подобрать M примерно равное ему, т. к. тогда α будет равняться 1-ому или ≈1-ому, следовательно, можно рассчитывать на оптимальное время, в лучшем случае равное O(1). В худшем случае все N элементов окажутся в одном списке, и тогда, например, операция нахождения элемента (в худшем случае) потребует O(N) времени. Закрытое хеширование (Открытая адресация) Первый метод назывался открытым, потому что он позволял хранить сколь угодно много элементов, а при закрытом хешировании их количество ограниченно размером хеш-таблицы. В отличие от открытого хеширования закрытое не требует каких-либо дополнительных структур данных. В ячейках таблицы хранятся не указатели, а элементы исходного массива, доступ к каждому из которых осуществляется по хеш-коду ключа, при этом одна ячейка может содержать только один элемент. Сам процесс заполнения хеш-таблицы с использованием алгоритма закрытого хеширования осуществляется следующим образом: имеется изначально пустая хеш-таблица T размера M, массив A размера N(M≥N) и хеш-функция h(), пригодная для обработки ключей массива A; элемент xi, ключ которого keyi, помещается в одну из ячеек хеш-таблицы, руководствуясь следующим правилом: если h(keyi) – номер свободной ячейки таблицы T, то в последнюю записывается xi; если h(keyi) – номер уже занятой ячейки таблицы T, то на занятость проверяется другая ячейка, если она свободна то xi заноситься в нее, иначе вновь проверяется другая ячейка, и так до тех пор, пока не найдется свободная или окажется, что все M ячеек таблицы заполнены. Последовательность, в которой просматриваются ячейки хеш-таблицы, называется последовательностью проб. Последовательность проб задается специальной функцией, например интервал между просматриваемыми ячейками может вычисляться линейно, или увеличиваться на некоторое изменяющееся значение. Последовательности проб Ниже приведены некоторые распространенные типы последовательностей проб. Сразу оговорим, что нумерация элементов последовательности проб и ячеек хеш-таблицы ведётся от нуля, а N — размер хеш-таблицы (и, как замечено выше, также и длина последовательности проб). Линейное пробирование: ячейки хеш-таблицы последовательно просматриваются с некоторым фиксированным интервалом k между ячейками (обычно, k = 1), то есть i-й элемент последовательности проб — это ячейка с номером (hash(x) + ik) mod N. Для того, чтобы все ячейки оказались просмотренными по одному разу, необходимо, чтобы k было взаимно-простым с размером хеш-таблицы. (Целые числа называются взаимно простыми, если они не имеют никаких общих делителей, кроме ±1.) На всякий: mod Деление c остатком (деление по модулю, нахождение остатка от деления, остаток от деления) Квадратичное пробирование: интервал между ячейками с каждым шагом увеличивается на константу. Если размер хеш-таблицы равен степени двойки (N = 2p), то одним из примеров последовательности, при которой каждый элемент будет просмотрен по одному разу, является: hash(x) mod N, (hash(x) + 1) mod N, (hash(x) + 3) mod N, (hash(x) + 6) mod N, … Двойное хеширование: интервал между ячейками фиксирован, как при линейном пробировании, но, в отличие от него, размер интервала вычисляется второй, вспомогательной хеш-функцией, а значит может быть различным для разных ключей. Значения этой хеш-функции должны быть ненулевыми и взаимно-простыми с размером хеш-таблицы, что проще всего достичь, взяв простое число в качестве размера, и потребовав, чтобы вспомогательная хеш-функция принимала значения от 1 до N — 1. Рассмотрим метод закрытого хеширования на примере построения хеш-таблицы. Положим, имеется целочисленный массив A, состоящий из 9 элементов: {A[key]=data, здесь key – ключ, data – некоторые данные} A[13]=8, A[56]=4, A[79]=1, A[37]=5, A[41]=2, A[76]=9, A[51]=3, A[93]=9, A[30]=1 Также есть хеш-таблица размера M=10, и хеш-функция h(key)=key%M (% – операция «остаток от деления»). Заполним хеш-таблицу элементами массив A: 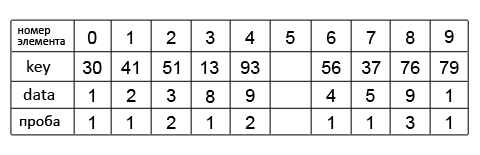 Для расстановки элементов использовалась выбранная формула. Подставив ключ, например первого элемента в нее получим: h(13) = 13 % 10 = 3, поэтому его номер в хеш-таблице 3. Последовательное добавление элементов приведет к возникновению коллизии при обработке элемента A[76]. Хеш-код его ключа 6, но в хеш-таблице ячейка с таким номером уже занята. Используя формулу линейного пробирования (тип последовательности проб) hi(key)=(h(key) +i) %M (i – число проверок, после первой проверки i=0), продолжим поиск свободной ячейки. Применим функцию при i=1: h1(76)=7; убедившись, что ячейка 7 занята, продолжаем поиск, увеличив i на 1: h2(76)=8. Ячейка 8 свободна, помещаем в нее элемент. Этот же метод используем и для всех остальных элементов. |
