ИГА. Понятие базы данных

• Название: Понятие базы данных
• Дата: 05.04.2022
• Размер: 0.77 Mb.
• Имя файла: ИГА.docx
• Тип: Документы; #445246
• страница: 13 из 37

Алгоритмы сортировки данных.

Сортировка пузырьком

Сортировка пузырьком (Bubble sort) является одним из самых простейших алгоритмов сортировки. Суть работы этого алгоритма в следующем: до достижения упорядоченности множества, алгоритм совершает проходы с попарным сравнением элементов. В том случае, если порядок не верен, то происходит обмен сравниваемых элементов местами. При каждом проходе, очередной наибольший элемент ставится перед предыдущим наибольшим элементом, а наименьший элемент перемещается на позицию выше (как бы «всплывает» до нужной позиции). Устойчивость алгоритма зависит от реализации. Алгоритм не требует дополнительного выделения памяти [1][7]. На рис. 35 приведён псевдокод алгоритма. Функция «swap» меняет элементы местами [9].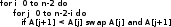



Сложность этого алгоритма O(n²)

Сортировка выбором

Алгоритм сортировки выбором (Selection Sort) интересен тем, что может быть реализован как устойчивый, так и не устойчивый. Алгоритм не требует дополнительного выделения памяти. Алгоритм работы проходит в три этапа³: [9][14]

1. 
   Поиск позиции минимального значения во множестве
   
2. 
   Если значения элементов не равны⁴, то меняем найденный элемент местами с первой неотсортированной позицией
   
3. 
   Запуск следующего прохода, исключая отсортированные элементы
   

Как уже было отмечено, алгоритм может быть устойчивым и неустойчивым. Зависит от проверки, которая выполняется на шаге 2. На рис. 40 приведён псевдокод устойчивого алгоритма.[6]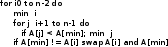



Этот алгоритм можно отнести к алгоритмам учебным, т.к. его сложность O(n²). Однако, его идея интереснее для изучения, чем в случае с сортировкой пузырьком, т.к. не требует многократных проходов по всему списку.

Сортировка вставками

Алгоритм сортировки вставками (Insertion sort) является последним учебным алгоритмом сортировки, который будет изучен. Примечательность этого алгоритма в том, что он может использовать список по мере его получения. [10][15]

Логика работы алгоритма в следующем: на каждом шаге выбирается один произвольный элемент из входных данных и вставляется его на нужную позицию в уже отсортированном списке. Так продолжается, пока входные данные не будут обработаны. Чтобы сделать алгоритм устойчивым, необходимо вставлять по порядку их появления во входных данных. В рис. 44 приведён псевдокод алгоритма. [9]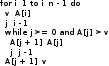



Сложность этого алгоритма соизмерима с двумя уже рассмотренными и составляет O(n²). Как и предыдущие алгоритмы, алгоритм эффективен на маленьких множествах. Особенность этого алгоритма – он более эффективен на частично упорядоченных множествах, т.к. обладает естественностью.

Сортировка слиянием

Алгоритм сортировки слиянием (Merge sort) является достаточно эффективным для использования на практике. Алгоритм интересен тем, что множество сначала разбивается на несколько подмножеств, прежде чем быть обработанным. Этот подход называется «разделяй и властвуй» или «метод декомпозиции». В зависимости от входных данных, алгоритм может применить рекурсивную обработку. Логику работы можно разбить на три основных шага: [6][16]

1. 
   Множество разбивается на 2 равные части (желательно)
   
2. 
   Каждая из частей сортируется отдельно (возможно рекурсивно этим же алгоритмом)
   
3. 
   Обе уже упорядоченные половины сливаются вместе
   

Алгоритм делится фактически на две функции: сортировку-слияние и слияние. На рис. 48 приведён псевдокод главной функции «сортировка-слияние». Важно заметить, что здесь используется рекурсивный подход и множество разбивается до тех пор, пока подмножество не составит два элемента. В том случае, если применяется рекурсивный подход, то алгоритм получается устойчивым и требует O(n) дополнительной памяти для хранения цепочек.[9]



В алгоритме, несмотря на дополнительную работу с массивами, важно то, что он достаточно эффективен и его сложность O(n log n). Эта сложность является хорошим показателем для универсального алгоритма. Алгоритм требует дополнительного резервирования памяти для своей работы в размере O(n).



В заключение: алгоритм может применяться на практике в силу своей гибкости. Конечно, при этом необходимо учитывать его особенности и требования к дополнительной памяти

Сортировка естественным слиянием

Алгоритм сортировки естественным слиянием является модификацией своего базового алгоритма «сортировка слиянием», поэтому, он использует те же принципы в своей основе. В данном параграфе будет приведена информация, которая относится только к «естественной» сортировке слиянием («Natural Merge Sort»).

Главное отличие этого алгоритма от базового в том, что он учитывает возможность того, что входные данные могут быть частично отсортированы. Этим достигается преимущество этого алгоритма на множествах, где данные заранее частично упорядочены [12].

Модифицированный алгоритм может быть формализован следующим образом [13]:

• 
  Множество разбивается части с уже от­сор­ти­ро­ван­ными эле­мен­тами (в худ­шем слу­чае, все части бу­дут со­сто­ять из од­но­го эле­мен­та, если эле­мен­ты множества идут по убы­ва­нию)
  
• 
  Производится слия­ние частей ме­то­дом сдваи­ва­ния
  

Для демонстрации того, что подход к написанию алгоритма может быть не только рекурсивным, в данном параграфе использован другой способ реализации алгоритма. Вторая особенность в том, что найденные отсортированные цепочки не хранятся в памяти компьютера, а алгоритм каждый раз проходит сначала в их поиске [14].

Реализация алгоритма большая по объёму, поэтому полный исходный код программы, реализующей алгоритм, приведён в приложении 4. Псевдокод функции, реализующей описанный алгоритм, приведён на рис. 55.



В заключение важно отметить, что сложность алгоритма составляет O(log n), что делает его очень эффективным на частично отсортированных множествах. На практике может потребоваться рекурсивная реализация алгоритма с дополнительным выделением O(n) памяти. Алгоритм рекомендуется к использованию в подходящих для сортировки вставками сценариях, но с частично упорядоченными входными данными

Сортировка подсчётом

Сортировка подсчётом (Counting sort) является алгоритмом, воплощающим идею «улучшения входных данных» (input enchantment) [9]. В других источниках можно встретить термин «предварительная обработка» (preprocessing) [11][12].

Суть идеи состоит в том, чтобы входящее множество (или его часть) обработать заранее, сохранить полученную дополнительную информация, которая потом поможет решить прямую задачу [9]. Этот алгоритм «улучшает» входное множество следующим образом: подсчитывает общее количество элементов меньших данного и заносит их в таблицу. После этого полученные числа указывают на позицию элемента в будущем отсортированном множестве. Таким образом, остаётся только скопировать элементы одного множества на соответствующие им позиции (на основе полученной таблицы) в упорядоченном множестве [13]. На рис.56 проиллюстрировано, как образуется эта таблица [9].



На рис 56. хорошо видно, как за несколько проходов получены будущие позиции элементов в упорядоченном множестве. В том случае, если будет велико разнообразие элементов, то алгоритм потеряет свои преимущества. Таким образом, диапазон значений элементов должен быть существенно меньше размера множества. Например, этот алгоритм будет эффективен на множестве А(x), где n = 1000, а x ϵ {0..10}. Это накладывает серьёзные ограничения на применение данного алгоритма. Ещё одна причина приведена ниже, после иллюстрации псевдокода на рис. 57. [6]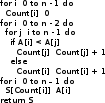



На основе этой реализации, есть другая, более совершенная, но и более сложная сортировка подсчётом распределения (distribution count) [9]. Она тесно связана с первой, поэтому её рассмотрение будет включено в рамки данного параграфа.

Для того чтобы не перезаписывать существующее множество, создаётся новое S на основе полученных данных. Элементы, чьи значения равны наименьшему возможному значению множества (обозначаются m(min)), копируются в первые F[0] элементов S. Элементы со значением m+1 в следующие позиции, т.е. F[0] … (F[0] + F[1]) – 1 и т.д. Метод сортировки получил своё название благодаря тому, что в статистике накапливание сумм частот называется «распределение» [1][9].

Изучая множество A(x) = {13, 11, 12, 13, 12, 12}, видно что, x ϵ {11, 12, 13}. Более удобно рассматривать входное множество справа налево. На рис. 60 приведён псевдокод алгоритма [9].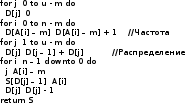



На рис. 61. процесс формирования результата. Важно заметить, что на вход алгоритм получает массив А, минимальное значение m и максимальное u[6].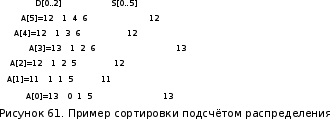



Как видно из примера, алгоритм выполняет два последовательных прохода по входным данным, а потому линеен, что является лучшим вариантом по эффективности. Однако это достигается тем, что есть информация о входных данных (минимальное и максимальное значения).

В заключение важно отметить, что сложность алгоритма составляет O(n + k) и в случае, если не применяется приём подсчёта распределения, то требуется O(n + k) дополнительной памяти, иначе O(k) и это делает алгоритм устойчивым. Алгоритм сортировки подсчётом распределения эффективен и рекомендуется к использованию в тех сценариях, когда объём входных данных не потребует выделения памяти, сверх допустимого размера

Сортировка Шелла

Автором алгоритма является Дональд Шелл и впервые этот алгоритм был опубликован в 1959 году. Д. Шелл разработал усовершенствование алгоритма сортировки вставками, сделав свой вариант пригодным для сортировки больших объёмов информации. В литературе этот алгоритм получил своё название «Сортировка Шелла» (Shell sort, Shell's method). Как и другие, рассмотренные в данной работе, алгоритмы, этот алгоритм имеет свои ограничения, которые будут рассмотрены после изучения псевдокода, работы и её результатов [3][4].

Логика работы алгоритма заметно усложнена, по сравнению с базовым алгоритмом: сначала сравниваются и сортируются значения, которые стоят друг от друга (во множестве) на расстоянии d (от выбора которого зависит сложность алгоритма). На втором проходе d уменьшается и заканчивается проходом с d = 1. При d = 1 сортировка получается обычным алгоритмом сортировки вставками. Вычисление d будет изучено далее. [6][18]

Теоретическое преимущество обусловлено тем, что в отличие от других алгоритмов (например «сортировка пузырьком») каждая перестановка значений уменьшает количество инверсий больше чем на 1. Так же видно, что алгоритм относится к неустойчивым, т.е. возможны случаи, когда алгоритм меняет местами одинаковые элементы. Так же алгоритм не требует выделения дополнительной памяти [8]. На рис. 62 приведён псевдокод, иллюстрирующий работу сортировки Шелла [9].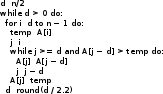



Как видно из схемы, алгоритм не обладает естественностью и устойчивостью, но он так же не требует выделения дополнительной памяти.

Важно отметить, что в псевдокоде приведён один из вариантов вычисления d. Это не единственный вариант, и можно оставить псевдокод без него, заменив d статичными числом. Однако для научной работы это было бы некорректно, т.к. не отражало бы важность вычисления расстояния.

Выбор длин промежутков dисключительно важен для времени работы алгоритма, поэтому ниже изучены основные методы вычисления, предложенные Шеллом, Хиббардом, Седжевиком, Праттом, Циура.

• 
  Шелл: d = n/2, d_i = d_i-1/2, d = 1. В худшем случае сложность составит O(n²)
  
• 
  Хиббард: (2ⁱ – 1)/2 ≤ n/2, i ϵ N. Сложность составит O(n^3/2)
  
• 
  Седжевик: Если i чётное: 9×2ⁱ – 9×2^i/2 + 1. Нечётное: 8×2ⁱ – 6×2^i/2 + 1. Средняя сложность составляет O(n^7/6), худшая: O(n^4/3). При использовании формулы Седжвика следует остановиться на значении inc[s-1], если 3*inc[s] > size.
  
• 
  Пратт: 2ⁱ×3^j ≤ n/2 где i, j ϵ N. Сложность составляет O(n (log n)²)
  
• 
  Циура: эмпирическим путём вычислил множество dϵ {1, 4, 10, 23, 57, 132, 301, 701, 1750}, лучшее для сортировки множества ёмкостью до 4000 элементов.
  
• 
  эмпирическая последовательность на числах Фибоначчи dϵ {F_n}
  

Быстрая сортировка

Быстрая сортировка (Quicksort, qsort) является одним из самых распространённых алгоритмов сортировки данных общего назначения. Алгоритм был представлен в 1960 году Информатиком Чарльзом Хоарой [3]. Алгоритм «Быстрая сортировка» относится к алгоритмам, которые реализуют подход «разделяй и властвуй». В рамках данной работы уже изучен один из таких алгоритмов – «Сортировка слиянием». Этот алгоритм может требовать выделения памяти (чтобы сделать обработку устойчивой). Подробно логика работы алгоритма будет описана ниже, но основная идея в следующем: выбрать опорный (pivot) элемент и сравнить все остальные элементы с опорным [18]. Затем на основании полученных данных разбить множество на несколько подмножеств по принципу «больше-меньше опорного». Повторить рекурсивно для подмножеств. На практике обычно применяется этот подход, но так же можно разбить множество по другому принципу: «больше-равно-меньше опорного». Подробное описание шагов: [6][7]

• 
  Выбирается некий элемент, который станет опорным. Для алгоритма не важен выбор, но для улучшения производительности этим элементом должна стать медиана (если возможно её узнать). Два основных подхода: всегда с одной и той же позиции (первый, последний и т.п.) или элемент со случайной позиции.
  
• 
  Разбивается множество так, чтобы все элементы большие или равные опорному оказались слева, а остальные справа. Обычный алгоритм операции:
  
  • 
    l = A[0], r = A[n-1]
    
  • 
    взятие опорного элемента m
    
  • 
    индекс l увеличивается, пока элемент A[l] < m
    
  • 
    индекс r уменьшается, пока элемент A[r] ≥ m
    
  • 
    Сравниваются l и
    
    • 
      Если l = r найдена середина массива и операция закончена, оба индекса указывают на опорный элемент
      
    • 
      Если l < r, тогда пару элементов нужно обменять местами и продолжить операцию с текущих значений l и r. Следует учесть, что если какой либо индекс дошёл до опорного элемента, то при обмене значение m изменяется на A[r] или A[l] элемент соответственно
      
• 
  Рекурсивно повторяется для получившихся подмножеств
  
• 
  Заканчивается рекурсия, когда множества состоят из одного или двух элементов. Первое (множество) возвращается в исходном виде, во втором (при необходимости) сортировка сводится к перестановке двух элементов. Все такие отрезки уже упорядочены в процессе разделения.
  

Как и в случае с алгоритмом «Сортировка слиянием», этот алгоритм тоже реализуют две функции. На рис. 66 приведён псевдокод функции, которая сортирует множество [9].



На рис. 67 приведён псевдокод функции, которая разбивает множество. Важно обратить внимание, что в данной реализации алгоритм неустойчивый и не требует выделения дополнительной памяти. Более того, была опущена проверка на пределы массива для i, которая может выйти за его пределы [9]. Это необходимо для сокращения объёма псевдокода.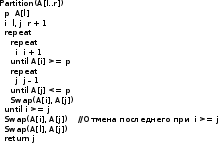



Скорость алгоритма зависит от входных данных и опорного элемента и является O(n log n) для среднего случая. Худший случай необходимо рассмотреть отдельно [1].

Возможна ситуация, когда на вход попало множество из большого количества элементов, после разбиения которого на две части, оказывается, что любой элемент в первом подмножестве упорядочен относительно любого элемента второго подмножества, а затем алгоритм рекурсивно применяется для каждого подмножества. В этом случае сложность алгоритма составит O(n²), что поставит его в один ряд по сложности с алгоритмами сортировки пузырьком, выбором, вставками и другими неэффективными алгоритмами. Это является худшим случаем. [6][11]