ИГА. Понятие базы данных
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
Задачи поиска в структурах данных.Алгоритмы поиска данных.Линейный поиск Этот вид алгоритма так же называется «Последовательный поиск» (Sequential search)[2]. Его применение достаточно широко в силу его простоты, и его можно найти, возможно, в каждом приложении для поиска данных в небольших массивах или коротких строках. Его суть очень проста: проход от элемента к элементу, пока значение элемента не станет равным ключу поиска. Конечно, этот алгоритм можно отнести к алгоритмам «грубой силы». На рис. 3 приведён псевдокод, реализующий этот алгоритм. [9] 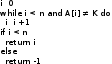 сложность алгоритма O(n) Прямой поиск подстроки Этот алгоритм изучается сразу после линейного поиска, т.к. он относится к тому же типу алгоритмов, т.е. «грубой силы» («Bruteforce») [3]. Единственная разница – ключ поиска. В этом случае требуется найти подстроку в строке. Достаточно частая задача в практическом программировании. Как и линейный поиск, этот алгоритм эффективен на небольших строках и может быть использован на практике. На рис. 6 приведён модифицированный алгоритм линейного поиска (новый тип ключа поиска). [9] 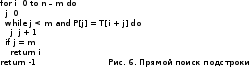 сложность алгоритма линейна и составляет O(n). В худшем случае сложность составит O(n×m). Двоичный поиск Этот алгоритм встречается под другим названием «Бинарный поиск» (Binary search). Своё название он получил, т.к. делит массив пополам, прежде чем начать поиск. Для этого алгоритма необходимо, чтобы массив был отсортирован. Логика работы алгоритма проста:[10] Ключ сравнивается со средним элементом и если они равны, то прекращает работу. Если нет, то: K < A[m], то поиск продолжается в первой половине массива K > A[m], то поиск продолжается во второй половине массива Для повышения эффективности, алгоритм должен быть рекурсивным, в противном случае его можно сделать смешанным и линейным поиском. На рис. 10 приведён псевдокод иллюстрирующий работу нерекурсивного алгоритма двоичного поиска [9]. 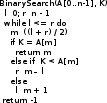 В заключение важно заметить, что этот алгоритм достаточно эффективен и его сложность варьируется в зависимости от входных данных[8]. Лучший случай O(1) Средний Значение найдено: O(log2(n – 1)) Значение не найдено: O(log2(n + 1)) Худший: O(log n) Алгоритм поиска в строке Кнута-Морриса-Пратта Есть два широко известных алгоритма, которые реализуют технику улучшения входного потока. Один из них это алгоритм Бойера-Мура (который так же будет изучен в рамках данной работы), а другой – алгоритм Кнута-Морриса-Пратта. Идея улучшения входного потока реализована алгоритмом следующим образом: ценой некоторого количества предварительных вычислений над шаблоном, шаблон сравнивается с исходным текстом не во всех позициях — часть проверок пропускаются как заведомо не дающие результата. [9][20] Алгоритм Кнута-Морриса-Пратта был опубликован в 1977 году. В основе обработки шаблона поиска лежит префикс-функция. [7] Префикс-функция вычисляет наибольшую длину наибольшего собственного суффикса подстроки, совпадающего с её префиксом. Например, для строки «abcabcd» результат работы префикс-функции: [0,0,0,1,2,3,0]. Таким образом: [8] у строки «a» нет префикса, совпадающего с суффиксом у строки «ab» нет префикса, совпадающего с суффиксом у строки «abc» нет префикса, совпадающего с суффиксом у строки «abca» префикс длины 1 совпадает с суффиксом у строки «abcab» префикс длины 2 совпадает с суффиксом у строки «abcabc» префикс длины 3 совпадает с суффиксом у строки «abcabcd» нет префикса, совпадающего с суффиксом Псевдокод алгоритма работы префикс-функции приведён на рис. 13 [9] 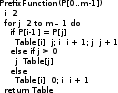 После вычисления таблицы алгоритм может приступить к поиску шаблона в строке. Псевдокод алгоритма приведён на рис. 15. На вход поступают: P – шаблон поиска. T – строка, в которой будет производиться поиск. Важно заметить, что Table – результат работы префикс-функции. [9]  В заключение важно отметить, что сложность алгоритма формируется двумя показателями: длиной шаблона (который обрабатывается заранее) и длиной строки. Поэтому, суммарная сложность составляет O(n + m) при условии, что шаблон не найден, т.к. иначе поиск закончится раньше. Средняя сложность составляет O(n / m). Важно отметить, что в формулах n – длина текста, m – длина шаблона. Алгоритм требует дополнительной памяти: O(m).[1][9] Как видно, нет выигрыша при работе с короткими строками, на которых линейный поиск может оказаться эффективнее, т.к. отсутствует предварительная работа с шаблоном Алгоритм поиска в строке Бойера-Мура Логика работы алгоритма схожа с алгоритмом Кнута-Морриса-Пратта, за исключением способа сравнивания шаблона и текста. В этом алгоритме сравнивание происходит справа-налево. Сначала совмещается начало текста с началом шаблона. Проверка начинается с последнего символа шаблона и движется справа-налево. Если все символы совпали – подстрока найдена, если встречается расхождение, то шаблон смещается вправо на величину d и проверка начинается заново. Величина смещения d вычисляется двумя способами [2][7]: Эвристика «стоп-символа» Эвристика совпавшего суффикса Эти названия используются в источнике [19], они просты и достаточно ёмки для отражения сути метода. В остальной литературе встречаются другие, более описательные названия, например «Построение таблицы сдвигов совпадающих суффиксов» [2][6][9][15]. Эвристика стоп-символа работает следующим образом: в случае несовпадения первого символа шаблона именно этот символ берётся в качестве «стоп-символа». В том случае, если части текста, которая сейчас обрабатывается, содержится «стоп-символ», то шаблон можно сдвинуть вправо так, чтобы символ в тексте (символ, равный стоп-символу) совпал с последним символом (равный стоп-символу) в шаблоне. [9][18]. На рис. 20 приведён пример работы этого случая. 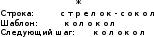 В том случае, если в обрабатываемом тексте нет символа, совпадающим со стоп-символом, тогда шаблон смещается на всю свою длину. На рис. 21 приведён пример этого случая. 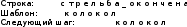 Однако в том случае, если стоп символ стоит за совпадающим символом, этот способ будет неэффективным и выполнит одну холостую проверку. На рис. 22 приведена иллюстрация. 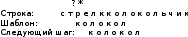 Для этого случая, есть второй метод вычисления смещения: Эвристика совпавшего суффикса. Если при сравнении строки и шаблона совпало один или больше символов, шаблон сдвигается в зависимости от того, какой суффикс совпал [18]. На рис. 23 проиллюстрирована работа этого способа. 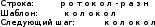 В данном случае совпал суффикс «окол», и шаблон сдвигается вправо до ближайшего «окол». Если подстроки «окол» в шаблоне больше нет, но он начинается на «кол», сдвигается до «кол». [18] Как уже было изучено и проиллюстрировано на примерах, алгоритм требует предварительной обработки шаблона, чтобы корректно его сдвигать в случаях совпадений: таблица стоп-символов и таблица суффиксов. Таблица стоп-символов строится по принципу последней позиции символа в шаблоне, кроме края шаблона. Например, для символа «а» в шаблоне «аоооаоа», последняя позиция – 4 (отсчёт начинается с нуля). Позиция на краю шаблона игнорируется из соображений быстродействия (в противном случае будут образовываться случаи, когда придётся лишний раз использовать эвристику совпавшего суффикса). [16][17] Таблица суффиксов больше по объему. Она строится исходя из следующего принципа: для каждого возможного суффикса S шаблона указываем наименьшую величину, на которую нужно сдвинуть вправо шаблон, чтобы он снова совпал с S. Если такой сдвиг невозможен, ставится |шаблон| (в обеих системах нумерации). Пример для шаблона =«abcdadcd» приведён на рис. 24. [1]: 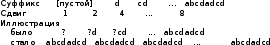 Если шаблон начинается и заканчивается одной и той же комбинацией букв, например «колокол», то эта комбинация («кол») вообще не появится в таблице. Алгоритм работы функции для вычисления таблиц сдвигов несложен, и на рис. 25 приведён её псевдокод.[6]  Как и ранее, в этом параграфе будет изучен базовый, упрощённый алгоритм, без модификаций, которые были предложены другими авторами. На рис. 26 приведён псевдокод алгоритма Бойера-Мура [9]. 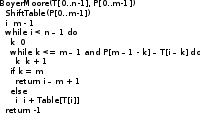 Важно отметить, что этот алгоритм широко используется на практике и, как остальные, имеет свои достоинства и недостатки [1][2][9]. К достоинствам алгоритма можно отнести: Алгоритм эффективен, особенно на текстах с естественным языком, где вероятность формирования «плохих» случаев ничтожно мала На платформе x86 есть аппаратные средства, которые могут быть использованы для оптимизации алгоритма. Например, после выполнения «rep cmpsb» в регистре ecx остаётся индекс не совпавшего символа, а указатели esi и edi указывают на соответствующие символы строк шаблона и текста. Недостатки: На коротких строках требование предварительной обработки ликвидирует выигрыш в скорости работы На больших алфавитах таблица стоп-символов занимает больше памяти На искусственно подобранных «неудачных» текстах (например, «колоколоколоколоколокол») скорость алгоритма Бойера-Мура серьёзно снижается Нужно заметить, что все достоинства алгоритма проявляются в сферах, где он применим. Недостатки же, напротив, не проявляются. Дело в том, что этот алгоритм лучше всего подходит для поиска различных шаблонов в изменяющихся строках на естественном языке. Желательно, чтобы алфавит был ограничен этим языком, а не содержал все возможные символы, как может предложить Юникод. [7] В том случае, если алгоритм реализуется на платформе, отличной от x86, то возможно, придётся оптимизировать работу алгоритма конкретно под платформу, если оптимизатор, предложенный средствами разработки, окажется неэффективным. [11][15] Алгоритм не применим во всех возможных сферах. В том случае, если строки коротки, особенно если шаблон по длине приближается к длине строки, то прямой поиск окажется эффективнее за отсутствием дополнительных предварительных обработок и относительно сложной логики. В том случае, если текст не меняется или меняется редко и, возможно, по расписанию (например, у поисковых машин), то будет эффективнее предварительно обработать сам текст, чтобы оптимизировать поиск. На больших объёмах статичного текста, эффективность алгоритмов, обрабатывающих предварительно текст, будет в разы выше, чем у алгоритма Бойра-Мура. [9][15] В заключение: алгоритм Бойера-Мура является одним из самых эффективных в своём классе. Поэтому он часто встречается в приложениях, но должен применяться с соблюдением ограничений, которые описаны ранее. Его сложность составляет O(n + m) для случая, если шаблон не найден. Для случая, если текст «неудачен», то сложность может достигать O(n × m). Средняя сложность составляет O(n / m). Здесь n – длина текста, m – длина шаблона. Алгоритм требует дополнительной памяти O(m + |∑|), где ∑ - алфавит |
