Методичка_графы. Понятие графа и его элементов. Типы графов Из истории развития теории графов
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
|
Напр.: е1 и е2 – строго параллельные дуги е3 и е4, е5 и е6 – пары нестрого параллельных дуг (!!) Нестрого параллельные дуги, отображающие ориентацию связи в обоих направлениях, по существу, равноценны неориентированной связи и могут быть заменены ребром. Опр. Граф, который содержит ребра и дуги, называется смешанным. Так, изображенный выше ориентированный граф можно изобразить в виде смешанного: v1 v2 v3 v5 v4 (!!) Всякий неориентированный граф можно превратить в ориентированный, заменив в нем каждое ребро на пару нестрого параллельных дуг. Опр. Если изменить направления всех дуг орграфа на противоположные, то получится орграф, обратный исходному. 5.2. Степени вершин орграфа В орграфе различают положительные 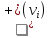 и отрицательные и отрицательные 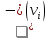 степени вершин, которые равны соответственно числу исходящих из vi и входящих в vi дуг. степени вершин, которые равны соответственно числу исходящих из vi и входящих в vi дуг. Напр.: 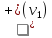 = 3 = 3 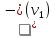 = 0 = 0v1 v2 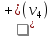 = 1 = 1 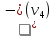 = 2 = 2v5 v4 v3 (!!) Очевидно, суммы положительных и отрицательных степеней всех вершин орграфа равны между собой и равны числу всех дуг. Опр. Вершина, 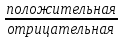 степень которой равна нулю, называется степень которой равна нулю, называется 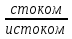 . . Так, v1 – исток, v5–сток (!!) Концевая вершина орграфа может быть либо стоком, либо истоком. 5.3. Ориентированные маршруты Маршруты на орграфе определяются аналогично, с той лишь разницей, что начальная вершина каждой последующей дуги маршрута должна совпадать с конечной вершиной предыдущей дуги. Иначе говоря, движение по маршруту допускается только в указанных направлениях (по направлению стрелок). Опр. Маршрут, не содержащий повторяющихся дуг, называется путем, а не содержащий повторяющихся вершин, - простым путем. Опр. Замкнутый путь называется контуром, а простой замкнутый путь – простым контуром. Опр. Орграф, содержащий хотя бы один контур, называется контурным. Задачи, связанные с маршрутами в орграфе, имеют большое практическое значение. Наиболее часто встает вопрос о минимальных и максимальных расстояниях и о числе маршрутов определенной длины. ПР. Дан орграф. Сколько в нем маршрутов длины 3? (8) 1 2 3 ● ● ● ● ● 4 5 5.4. Связность орграфов Связность орграфов определяется так же, как и для неориентированных (без учета направлений дуг). Специфичным для орграфа является понятие сильной связности. Опр. Орграф называется сильно связным, если для любой пары вершин существует путь из одной вершины в другую и обратно. Напр.: Опр. Компонентами сильной связности орграфа называются его максимальные по включению сильно связные подграфы. На данном примере изображен орграф, для которого найдены все три компоненты сильной связности (закрашенные области, обведенные пунктиром). 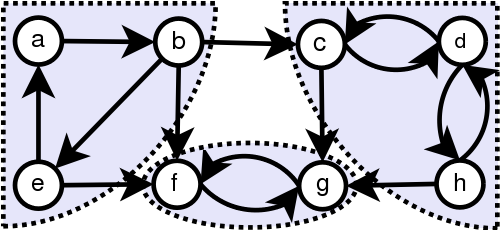 5.5. Матрица смежности орграфа Каждую дугу орграфа ек представляют как упорядоченную пару вершин (vi; vj), при этом (i; j) - элемент матрицы смежности равен числу дуг, направленных от вершины vi к вершине vj. Напр.: v1 е v2 e3 e4 e1 e2 е8 e5 v3 e6 v5 е9 v4
(!!)Матрица смежности орграфа, в общем случае, несимметрична. Петлям соответствуют единицы на главной диагонали. Нулевая строка и нулевой столбец с тем же номером соответствуют изолированной вершине. 5.6. Матрица инцидентности орграфа В случае орграфа ненулевой элемент матрицы инцидентности равен +1, если vi – начальная вершина дуги еj, и равен -1, если vi – конечная вершина дуги еj. В клетке, соответствующей петле, ставится 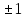 . .Напр.: Матрица смежности для приведенного выше орграфа имеет вид:
5.7. Графы и бинарные отношения Пусть на множестве Х задано бинарное отношение R. Ему соответствует ориентированный граф, вершины которого изображают элементы из Х, а дуга (xi; xj) существует тогда и только тогда, когда xi R xj. Если имеют место соотношения xi R xj и xj R xi, то вершины связываются 2-мя нестрого параллельными дугами, которые можно заменить ребром. Таким образом, симметричному отношению соответствует неориентированный граф. Соотношению xi R xi соответствует петля, выходящая из xi и входящая в ту же вершину. Значит, если R рефлексивно, то соответствующий граф имеет петли во всех вершинах. Если R транзитивно, то в графе для каждой пары рёбер (xi; xj) и (xj; xk) имеется замыкающее ребро (xi; xk). Если бинарное отношение х R у устанавливает связь между элементами х 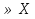 и элементами у и элементами у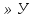 , то граф такого отношения будет ориентированным биграфом. , то граф такого отношения будет ориентированным биграфом.Рассмотрим теперь соответствие между операциями над отношениями и операциями над графами. Для каждого отношения R существует обратное ему отношение R-1, граф которого отличается от графа отношения R тем, что направления всех дуг заменены на противоположные. 6. Деревья 6.1. Понятие дерева. Свойства свободных деревьев Опр. Связный ациклический граф называется деревом. (!!) Очевидно, что деревья не имеют петель и кратных ребер, т.е. являются простыми графами. Среди различных деревьев выделяют 2 важных частных случая:
ПР. а) Различные свободные деревья с 4-мя вершинами: б) Различные свободные деревья с 5-ю вершинами: в) Различные свободные деревья с 6-ю вершинами: Очевидно:
Опр. Несвязный граф, компонентами которого являются деревья, называется лесом. (!!) Лес из к деревьев, содержащий р вершин, имеет в точности р – к ребер. Опр. Остовным деревом (остовом, каркасом или скелетом) неориентированного графа G называется его подграф, содержащий все вершины графа и являющийся деревом. Ребра графа, не входящие в остов, называются хордами графа относительно остова. 6.2. Дерево с корнем, ветви дерева Если в дереве отметить некоторую вершину 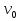 , то ее называют корнем дерева, а само дерево – деревом с корнем. , то ее называют корнем дерева, а само дерево – деревом с корнем.Обозначая вершины, смежные с вершиной v0 соответственноv1, v2,…, с v1 – v11, v12,…,а с v2 – v21, v22,…и т.д., можно построить дерево с корнем. (!!) Очевидно, что каждая вершина дерева может служить его корнем. Если v – вершина дерева с корнем v0, тогда множество всех вершин, связанных с корнем цепями, проходящими через вершину v, порождает подграф, который называется ветвью вершины v в дереве с корнем v0. Очевидно, что эта ветвь связна и сама является деревом с корнем в этой вершине v. 6.3. Типы вершин и центры деревьев Пусть дано конечное дерево G. Все его концевые вершины называются вершинами типа 1.Если удалить из графа все такие вершины вместе с инцидентными им ребрами, то получится подграф G, который будет деревом. Концевые вершины дерева G называются вершинами типа 2 в дереве G. Аналогично определяются вершины типов 3, 4, и т.д. Ясно, что в конечном дереве G имеются вершины лишь конечного числа типов. Опр. Вершины максимального типа называются центрами дерева. (!!)Дерево имеет либо 1, либо 2 центра. Опр. Каждая цепь, соединяющая центр дерева с его концевой вершиной, называется радиальной, а цепь, соединяющая две концевые вершины дерева и проходящая через его центр или оба центра (если их два), - диаметральной цепью. (!!) Если в дереве 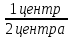 , то длина диаметральной цепи равна , то длина диаметральной цепи равна  , где к – максимальный тип вершин дерева. , где к – максимальный тип вершин дерева.6.4. Ориентированное дерево Опр. Ориентированное дерево называется прадеревом с корнем v0, если существует путь между вершиной v0и любой другой его вершиной. (!!) Прадерево имеет единственный корень, и все ребра в нем имеют направление от корня. При этом в каждую вершину ордерева входит только одно ребро. Опр. Концевая вершина ордерева называется листом. Опр. Путь из корня в лист называется ветвью. Опр. Длина наибольшей ветви ордерева называется его высотой. Опр. Уровнем вершины ордерева называется расстояние от корня до этой вершины. Вершины одного уровня образуют ярус дерева. (!!) Корень имеет уровень равный 0. Опр. Если изменить направления всех ребер ордерева на противоположные (к корню), то получится орграф, который называется сетью сборки. 6.5. Бинарные деревья Опр. Бинарным (двоичным) деревом называется ориентированное дерево, в котором каждая вершина (узел) имеет не более двух потомков. Бинарное дерево имеет корень и два непересекающихся подмножества, каждое из которых само является бинарным деревом. Эти подмножества называются правым и левым поддеревьями исходного дерева. Напр.: Для практических целей, обычно, используют два подвида бинарных деревьев: двоичное дерево поиска и двоичная куча. Опр. Двоичное дерево называется двоичным деревом поиска, если его элементы расположены так, что для каждого элемента n все элементы в левом поддереве n будут меньше, чем n, а все элементы в правом поддереве - больше, чем n. В общем случае существует огромное число двоичных деревьев поиска (различной формы) для любого заданного набора элементов. Напр.: Три двоичных дерева поиска с одним и тем же набором элементов (2, 3, 5, 7, 8) 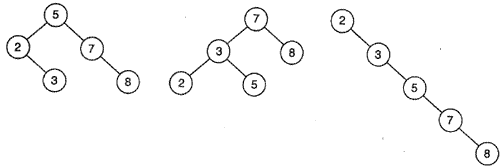 |
