Методичка_графы. Понятие графа и его элементов. Типы графов Из истории развития теории графов
 Скачать 0.79 Mb.
|
|
ПР. Предположим, что нужно сформировать двоичное дерево, узлы (элементы) которого имеют следующие значения признака: 20, 10, 35, 15, 17, 27, 24, 8, 30. В этом же порядке они и будут поступать для включения в двоичное дерево. 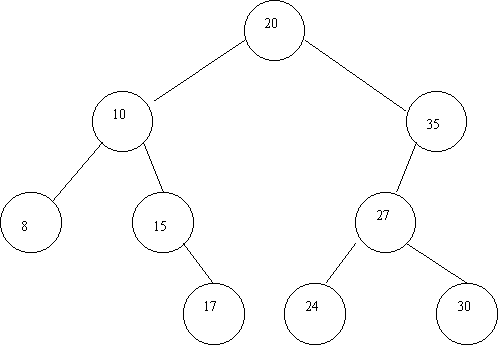 Опр. Двоичная куча (пирамида) - это такое двоичное дерево, для которого выполнены три условия: - Значение в любой вершине больше, чем значения ее потомков. - Все слои, кроме, может быть, последнего, заполнены полностью. - Последний слой заполняется слева направо. Пусть структура данных для хранения двоичной кучи имеет вид 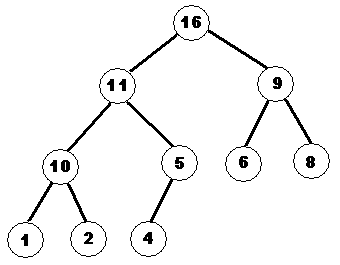  Существуют также кучи, где значение в любой вершине, наоборот, меньше, чем значения ее потомков. 7. Взвешенные графы. Раскраска графов Часто, особенно когда графы используются для моделирования реальных систем, их вершинам, или ребрам, или и тем, и другим приписываются некоторые числа. Природа этих чисел может быть самая разнообразная. Например, если граф представляет собой модель железнодорожной сети, то число, приписанное ребру, может указывать длину перегона между двумя станциями, или наибольший вес состава, который допустим для этого участка пути, или среднее число поездов, проходящих через этот участок в течение суток и т.п. Что бы ни означали эти числа, сложилась традиция называть их весами, а граф с заданными весами вершин и или ребер - взвешенным графом. В графе можно взвесить вершины таким образом, что каждой вершине будет сопоставлено целое число. Если числа трактовать как номера краски, то такое взвешивание вершин называют вершинной раскраской графа. Раскраска называется правильной, если никакие смежные вершины не окрашены в один цвет. Раскраска графа, в которой используется минимальное число красок, называется минимальной. Число красок минимальной раскраски является одной из характеристик графа и называется хроматическим числом. Так, например, хроматическое число биграфа равно 2. Двум равно и хроматическое число любого дерева. Дерево – биграф? С задачей определения минимальной раскраски графа связана известная проблема четырех красок: «Пусть имеется географическая карта. Можно ли, используя только 4 краски, изобразить эту карту так, чтобы соседние страны (имеющие общую границу) были окрашены в разный цвет?» (В соответствующем графе вершинами являются страны, а смежными вершинами являются соседние страны. После 1976 года ответ на этот вопрос является положительным.) В теории графов ставится часто вопрос о реберной раскраске графов. Какое минимальное число цветов (это число иногда называют реберно-хроматическим) нужно, чтобы раскрасить ребра графа так, что любые 2 ребра, имеющие общую вершину, были бы окрашены в разный цвет? Для реберно-хроматического числа графа верна следующая теорема Визинга: Если в графе максимальная степень вершин равна r, то реберно-хроматическое число равно либо r, либо r +1. Опр. Минимальное остовное дерево в связанном, взвешенном, неориентированном графе - это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него ребер. Задача о нахождении минимального остовного дерева часто встречается в подобной постановке: допустим, есть n городов, которые необходимо соединить дорогами, так, чтобы можно было добраться из любого города в любой другой (напрямую или через другие города). Разрешается строить дороги между заданными парами городов и известна стоимость строительства каждой такой дороги. Требуется решить, какие именно дороги нужно строить, чтобы минимизировать общую стоимость строительства. Эта задача может быть сформулирована в терминах теории графов как задача о нахождении минимального остовного дерева в графе, вершины которого представляют города, ребра - это дороги, которые можно проложить напрямую между двумя городами, а вес ребра равен стоимости строительства соответствующей дороги. Напр.: 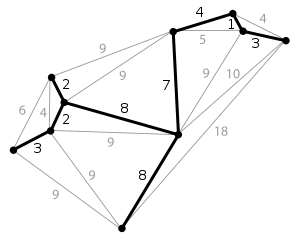 8. Приложения теории графов в различных областях науки и техники8.1. Графы и информация Двоичные деревья играют весьма важную роль в теории информации. Предположим, что определенное число сообщений требуется закодировать в виде конечных последовательностей различной длины, состоящих из нулей и единиц. Если вероятности кодовых слов заданы, то наилучшим считается код, в котором средняя длина слов минимальна по сравнению с прочими распределениями вероятности. Задачу о построении такого оптимального кода позволяет решить алгоритм Хаффмана. Двоичные кодовые деревья допускают интерпретацию в рамках теории поиска. Каждой вершине при этом сопоставляется вопрос, ответить на который можно либо "да", либо "нет". Утвердительному и отрицательному ответу соответствуют два ребра, выходящие из вершины. "Опрос" завершается, когда удается установить то, что требовалось. Таким образом, если кому-то понадобится взять интервью у различных людей, и ответ на очередной вопрос будет зависеть от заранее неизвестного ответа на предыдущий вопрос, то план такого интервью можно представить в виде двоичного дерева. 8.2. Графы и химия Еще А. Кэли рассмотрел задачу о возможных структурах насыщенных (или предельных) углеводородов. Все атомы углеводорода четырехвалентны, все атомы водорода одновалентны. Молекула каждого предельного углеводорода представляет собой дерево. Если удалить все атомы водорода, то оставшиеся атомы углеводорода также будут образовывать дерево, каждая вершина которого имеет степень не выше 4. Следовательно, число возможных структур предельных углеводородов, т. е. число гомологов данного вещества, равно числу деревьев с вершинами степени не больше четырех. Таким образом, подсчет числа гомологов предельных углеводородов также приводит к задаче о перечислении деревьев определенного типа. Эту задачу и ее обобщения рассмотрел Д. Пойа. 8.3. Графы и биология Деревья играют большую роль в биологической теории ветвящихся процессов. Для простоты мы рассмотрим только одну разновидность ветвящихся процессов - размножение бактерий. Предположим, что через определенный промежуток времени каждая бактерия либо делится на две новые, либо погибает. Тогда для потомства одной бактерии мы получим двоичное дерево. Нас будет интересовать лишь один вопрос: в скольких случаях n-е поколение одной бактерии насчитывает ровно k потомков? Рекуррентное соотношение, обозначающее число необходимых случаев, известно в биологии под названием процесса Гальтона-Ватсона. Его можно рассматривать как частный случай многих общих формул. 8.4. Графы и физика Еще недавно одной из наиболее сложных и утомительных задач для радиолюбителей было конструирование печатных схем. Печатной схемой называют пластинку из какого-либо диэлектрика (изолирующего материала), на которой в виде металлических полосок вытравлены дорожки. Пересекаться дорожки могут только в определенных точках, куда устанавливаются необходимые элементы (диоды, триоды, резисторы и другие), их пересечение в других местах вызовет замыкание электрической цепи. В ходе решения этой задачи необходимо вычертить плоский граф, с вершинами в указанных точках. Задания для самостоятельного решения
Контрольные вопросы
2014 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
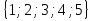задано бинарное отношение R = 
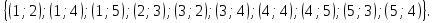Для данного отношения запишите область определения и область значений. Нарисуйте граф этого отношения. Составьте для него матрицу смежности и инцидентности.