Методичка_графы. Понятие графа и его элементов. Типы графов Из истории развития теории графов
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
|
частью графа G = (V; E), если V V и Е Е. Опр. Часть графа, которая не содержит изолированные вершины, называется подграфом. Опр. Часть графа, которая, наряду с некоторым подмножеством ребер графа, содержит и все вершины графа, называется суграфом. Напр.: v3 v3 v2 e2 v3 v2 e2 v2 e2 v2 e2 v3 e6 е7 e3 e6 e1 e1 e1 e4 v1 v4 v1e5 v1 v1 v4 граф часть графа подграф суграф Пусть даны две части графа G: G1 и G2 1. Объединение графов – это граф G = G1 U G2, множества вершин и ребер которого определяются так: V = V1 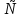 V2, E = E1 V2, E = E1 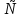 E2. E2.2. Пересечение графов – это граф G = G1 ∩ G2, множества вершин и ребер которого определяются так: V = V1  V2, E = E1 V2, E = E1  E2. E2.Если V1  V2 = V2 = 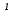 и E1 и E1  E2 = E2 = 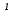 , то графы называются непересекающимися , то графы называются непересекающимися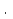 3. Сложение по модулю 2 – это граф G = G1 ⊕ G2, множество вершин которого V = V1 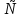 V2, а множество ребер E = (E1 V2, а множество ребер E = (E1 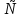 E2) \ (E1 E2) \ (E1  E2). E2).Напр.: Найдем G1 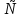 G2, G1 G2, G1  G2 и G1 ⊕ G2, если - части графа G2 и G1 ⊕ G2, если - части графа G1 v3 G2 v3 v2 v2 v1 v1 v4 v4 G1 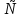 G2 v3 G1 G2 v3 G1  G2 v3 G2 v3v2 v2 v1 v1 ● v4 v4 G1 ⊕ G2 v3 v2 v1 v4 4. Дополнение графа Пусть G - часть графа G, тогда совокупность всех ребер графа G, не принадлежащих его части G, вместе с инцидентными вершинами образует дополнение частиG до графа G. Так, дополнением для G2 будет граф: v3 v2 v4 3. Маршруты. Связность графов. Эйлеровы и гамильтоновы графы 3.1. Маршруты, цепи и циклы Опр. Маршрутом длины т называется последовательность т ребер графа (не обязательно различных) таких, что два соседних ребра имеют общую вершину. e2 Напр.: v2 e3 v3 v1 e1 e6 e4 v4 v5 e5
Опр. Маршрут, все ребра которого различны, называется цепью, а маршрут, для которого различны все вершины, называетсяпростой цепью. Напр.: (е2; е4; е6) – цепь (е1; е2; е4) – простая цепь Опр. Маршрут, который приводит в ту же вершину, из которой начался, называется замкнутым. Опр. Замкнутая цепь называется циклом, а простая замкнутая цепь – простым циклом. Напр.: (е2; е4; е5; е6) – цикл (е3; е6; е4) – простой цикл Опр. Граф называется циклическим, если он содержит хотя бы один цикл, в противном случае он называется ациклическим. (!!) Очевидно, что мультиграфы и псевдографы являются циклическими. 3.2. Связность и разделимость графов Опр. Две вершины графа называется связанными, если существует маршрут, соединяющий эти вершины. Граф, любая пара вершин которого связана, называется связным графом. Очевидно, в связном графе между любыми двумя вершинами существует простая цепь, т.к. из связывающего их маршрута всегда можно удалить циклический участок, проходящий через некоторую вершину более одного раза. Если граф несвязный, то множество его вершин можно единственным образом разделить на непересекающиеся подмножества, каждое из которых содержит все связанные между собой вершины и вместе с ребрами образует связный подграф. Такие подграфы называются компонентаминесвязного графа. Напр.: Связный Несвязный Связный граф можно разделить на несвязные подграфы, если удалить из него некоторые вершины и ребра. При удалении вершин исключаются и все ребра, для которых эта вершина является граничной, при удалении же ребер вершины сохраняются. Опр. Вершина, удаление которой превращает связный граф в несвязный, называется точкой сочленения. Ребро с такими свойствами называетсямостом. (!!) При наличии моста в графе имеются, по крайней мере, одна точка сочленения. Напр.: точки сочленения мост точка сочленения Опр. Связный граф называется разделимым, если он имеет хотя бы одну точку сочленения, в противном случае граф называется неразделимым. 3.3. Эйлеровы графы Эйлеров цикл можно считать следом пера, вычерчивающего этот граф, не отрываясь от бумаги. Т.о., эйлеровы графы – это такие графы, которые можно изобразить одним росчерком пера, причем процесс такого изображения начинается и заканчивается в одной и той же точке. Напр.: Т1. (Эйлера) Конечный неориентированный граф эйлеров тогда и только тогда, когда он связен и степени всех его вершин четны. Можно поставить задачу и об отыскании цепи, которая бы начиналась в одной вершине, оканчивалась в некоторой другой вершине и проходила бы по всем ребрам в точности по одному разу. Такие цепи называется эйлеровыми. Т2.Для того чтобы на связном граф имелась эйлерова цепь, необходимо и достаточно, чтобы в графе были ровно две нечетные вершины, которые и были бы концами этой цепи. Напр.: 3.4. Гамильтоновы линии Опр. Простой цикл, который проходит через все вершины графа, называется гамильтоновым. В отличие от эйлерового этот цикл не покрывает всех ребер графа. Напр.: Если критерий существования эйлерового цикла очень прост, то для гамильтоновых циклов никакого общего правила не найдено. 4. Матричный способ задания графов Отношение смежности на множестве вершин можно определить, представив каждое ребро как пару смежных вершин, т.е. ek = (vi; vj) = (vj; vi) 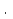 Очевидно, что петля при вершине vi представляется парой (vi; vi.). Множество вершин V вместе с определенным на нем отношением смежности полностью определяет граф. При этом граф можно представить матрицей смежности, строки и столбцы которой соответствуют вершинам графа, а ее (i; j) - элемент равен числу кратных ребер, связывающих вершины vi и vj. Напр.: Для графа e2 v2 e3 v3 v1 e1 e6 e4 v4 v5 e5 матрица смежности имеет вид:
(!!)1 Матрица смежности симметрична относительно главной диагонали. В столбцах и строках, соответствующих изолированной вершине, все элементы равны нулю. Петле соответствует «2» на главной диагонали. (!!)2 Элементы матрицы простого графа равны нулю или единице, причем все элементы главной диагонали нулевые. 4.2. Матрица инцидентности Рассматривая инцидентность вершин и ребер (p; q) – графа, можно представить его матрицей инцидентности размера p  q, строки которой соответствуют вершинам, а столбцы – ребрам. Элементы этой матрицы определяются по правилу: (i; j) - элемент равен 1, если вершина vi инцидентна ребру еj, и равен 0, если vi и еj не инцидентны. q, строки которой соответствуют вершинам, а столбцы – ребрам. Элементы этой матрицы определяются по правилу: (i; j) - элемент равен 1, если вершина vi инцидентна ребру еj, и равен 0, если vi и еj не инцидентны.Так, для изображенного в предыдущем пункте графа матрица инцидентности имеет вид:
(!!) Каждый столбец матрицы инцидентности содержит два единичных элемента. Если в вершине vi имеется петля, то в соответствующей клетке ставится цифра 2. Нулевая строка соответствует изолированной вершине. 4.3. Список ребер Это еще один способ задания графа. Каждая строка этого списка соответствует ребру: в ней записаны номера вершин, инцидентных ему. Для рассмотренного выше графа список ребер можно записать следующим образом:
5. Ориентированные графы 5.1. Понятие ориентированного графа Часто связи между объектами характеризуются вполне определенной ориентацией. Например, на некоторых улицах допускается одностороннее движение, ток по проводам течет в одном направлении. Вершины соответствующих графов оказываются неравноправными, они рассматриваются в определенном порядке. При этом каждому ребру можно приписать направление от первой из вершин ко второй. Для указания направления соответствующее ребро отмечается стрелкой. Опр. Направленные ребра называется дугами, а граф, содержащий их, - ориентированным графом. Первая по порядку вершина дуги называется ее началом, вторая – концом. Напр.: v1 е7 v2 e3 e4 e1 e2 е8 e5 v3 e6 v5 е9 v4 Опр. Две кратные дуги называются строго параллельными, если они одинаково направлены, и нестрого параллельными, если противоположно направлены. |
