Методичка_графы. Понятие графа и его элементов. Типы графов Из истории развития теории графов

• Название: Понятие графа и его элементов. Типы графов Из истории развития теории графов
• Дата: 06.03.2019
• Размер: 0.79 Mb.
• Имя файла: Методичка_графы.docx
• Тип: Решение; #69683
• страница: 1 из 4

1. 
   Понятие графа и его элементов. Типы графов
   

1.1. Из истории развития теории графов


A
Первая работа по теории графов была опубликована Л. Эйлером в 1736 году. Она содержала решение задачи о кенигсбергских мостах: «Можно ли совершить прогулку по городу таким образом, чтобы выйдя из любого места города, вернуться в него, пройдя в точности один раз по каждому мосту?»


A


B

D

B

D


C

C


Т.к. неважно, как проходит путь по частям суши, то их можно представить точками. А так как связи между этими частями осуществляются только через 7 мостов, то каждый из них можно изобразить некоторой линией, соединяющей соответствующие точки. В результате получается граф.

Эйлер дал отрицательный ответ на поставленный вопрос. Более того, он доказал, что подобный маршрут имеется только для такого графа, каждая из вершин которого связана с четным числом ребер.

Вначале теория графов имела дело в основном с математическими развлечениями и головоломками. Но уже в 19 веке графы стали использоваться при решении ряда важных практических проблем: при построении схем электрических цепей, молекулярных схем, при решении транспортных задач. Несмотря на это, теория графов как математическая дисциплина сформировалась только в 30-х годах 20 века, когда венгерский математик Денеш Кёниг ввел понятие «граф».

Теория графов тесно связана с такими разделами математики, как теория множеств, теория матриц, математическая логика и теория вероятностей. Во всех этих разделах графы применяют для представления различных математических объектов, и в то же время сама теория графов широко использует аппарат родственных разделов математики. Теория графов располагает также мощным аппаратом решения прикладных задач из самых разных областей науки и техники: в программировании, экономике, психологии, биологии.
1.2. Понятие графа. Элементы графа

Опр. Графом называется совокупность 2-х множеств: V (точек) и E (линий, соединяющих какие-либо две точки). Элементы множества V называются вершинами графа, а элементы множества E - его ребрами.

Обозначение: G

Напр.: Построим граф игр, сыгранных командами, если в соревнованиях участвуют 6 команд А, B, C, D, E и F, причем некоторые команды уже сыграли друг с другом:

А – с C, D, F; B – c C, E, F; C – c A, B;

B

C

D

F

E

A

D – c A, E, F; E – c B, D, F; F – c A,B, D, E.

Из рисунка видно, какие команды еще не играли друг с другом.

(!!) Точки пересечения некоторых ребер графа могут не являться его вершинами. Поэтому вершины графа должны отличаться отчетливо.

Опр. Две вершины, которые соединяет ребро графа, называются граничными вершинами этого ребра и являются смежными.

При этом говорят, что вершины инцидентны ребру.

Опр. Ребро, граничные вершины которого совпадают, называется петлей.

●

Опр. Ребра с одинаковыми граничными вершинами называются кратными.

Их можно изобразить так: 3

Опр. Вершины, которые не имеют инцидентных ребер, называются изолированными вершинами.

Напр.: В графе:

e₁ v₃ е₆ – петля

v₂ e₂ е₂и е₃ – кратные ребра

v₁e₁e₄e₅v₄v₄ – изолированная вершина

v₃и v₅ –

v₅ e₆
1.3. Типы графов

Опр. Если множества V и E конечны, то граф называется конечным. Конечный граф, содержащий p вершин и q ребер, называется (p; q) – графом.

Опр. Граф, состоящий только из изолированных вершин, называется пустым или нуль-графом.

Обозначение: О_п, где п – число вершин

Напр.:

О₁ -  О₂ -   О₃ -   О₄ -  

  

Опр. Граф без петель и кратных ребер называется простым.

Опр. Простой граф, в котором любые две вершины соединены ребром, называется полным.

Обозначение: U_п, где п – число вершин

Напр.:
U₂ - U₃ - U₄ -

Опр. Если множество вершин простого графа V допускает такое разбиение на два непересекающиеся подмножества V₁ и V₂ , что не существует ребер, соединяющих вершины одного и того же подмножества, то он называется двудольнымили биграфом.

Напр.:

V₁ V₂

Опр. Граф без петель, но с кратными ребрами называется мультиграфом.

Опр. Граф, содержащий хотя бы одну петлю, называется псевдографом.

(!!) В псевдографе могут быть кратные ребра.
1.4. Степень вершины. Однородные графы

Опр. Число ребер, инцидентных вершине, называется степенью вершины.

Обозначение: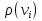

(!!) При подсчете степени вершины петля учитывается дважды.

Так, для графа игр: (А) = (В) = (Д) =(Е) = 3, (F) = 4, (C) = 2.

Опр. Вершины, степени которых являются четными числами, называются четными вершинами. Вершины с нечетной степенью называются нечетными.

Опр. Вершина, степень которой равна 1, называется концевой вершиной.

(!!) Очевидно, что:

1) степень изолированной вершины равна 0;

2) сумма степеней всех его вершин равна удвоенному числу ребер, т.е. является четным числом;

3) число нечетных вершин любого графа четно.

Опр. Граф, степени вершин которого одинаковы и равны r, называется однородным степени r.

Напр.:

- однородный степени 3 (полный)

- однородный степени 4 (неполный)


(!!) Полный граф с п вершинами – всегда однородный степени (п – 1), а пустой граф – однородный степени 0.

1.5. Изоморфные графы

Один и тот же граф можно изобразить по-разному, т.к. вершины можно располагать на плоскости произвольно и ребра рисовать либо прямыми линиями, либо кривыми.


A
Так, например, три графа, изображенные на рисунках,


E
A

F

B

C

D

E

B

C

D

F

E

A


D



C



F

B


в некотором смысле, один и тот же граф, т.к. они содержат одну и ту же информацию.

Опр. Два графа называются изоморфными, если они имеют одно и то же число вершин, и для любых 2-х вершин первого графа, соединенных ребром, соответствующие им вершины второго графа тоже соединены ребром и обратно.

Нередко приходится решать вопрос о том, являются ли два данных графа изоморфными. Иногда сразу ясно, что это не так. Например, графы

не могут быть изоморфными, т.к. они имеют разное число вершин.

Не могут быть изоморфными и графы

т.к. у них неодинаковое число ребер.

Однако, если сразу не видно, как доказать, что два графа не изоморфны, то вопрос об их изоморфности может оказаться довольно трудным. Например, рассмотрим два изоморфных графа:


1

1


2

3

4

5

6

7


5

4



2

7



6

3


Их изоморфность становится очевидной только после соответствующего обозначения их вершин.

1.6. Плоские и неплоские графы

Сравним два изоморфных графа, изображенных на рисунках:

На первом из них ребра пересекаются в точке, не являющейся вершиной графа, на втором – все точки пересечения ребер графа служат его вершинами.

Опр. Граф называется плоским, если его ребра не пересекаются в точках, отличных от вершин данного графа.

Опр. Граф называется планарным, если существует изоморфный ему плоский граф, т.е. если его можно изобразить на плоскости таким образом, чтобы его ребра пересекались только в вершинах.

Так, граф, изображенный на первом рисунке, является планарным, т.к. существует изоморфный ему граф, не имеющий лишних точек пересечения.

Примерами плоских графов являются карты дорог, планы городов, где улицы служат ребрами, а площади и уличные перекрестки – вершинами. Еще одним примером применения плоских графов служит построение схем электрических цепей. Так, один из наиболее эффективных способов массового производства стандартных электрических схем для радио- и телевизионных приемников состоит в том, что схема наносится печатным способом в виде металлической фольги на бумажную или пластмассовую основу. Однако, для того чтобы оно было осуществимо, граф рассматриваемой сети проводов должен иметь плоское представление, ведь пересечение 2-х ребер привело бы к короткому замыканию в системе.

Задача о трех колодцах. Можно ли от каждого из 3-х домов проложить тропинку к каждому из 3-х колодцев так, чтобы тропинки не пересекались?
● ● ●

● ● ●

Задача не может быть решена положительно, т.к. граф этой задачи не является плоским.
2. Части графа. Операции с частями графа

Опр. Граф G = (V; E) называется