ответы. Понятие нейрокомпьютера. Виды нейрокомпьютеров
 Скачать 1.89 Mb. Скачать 1.89 Mb.
|
|
Сети Хопфилда. Структура. Принцип работы. Сеть Хопфилда использует три слоя: входной, слой Хопфилда и выходной слой. Каждый слой имеет одинаковое количество нейронов. Входы слоя Хопфилда подсоединены к выходам соответствующих нейронов входного слоя через изменяющиеся веса соединений. Выходы слоя Хопфилда подсоединяются ко входам всех нейронов слоя Хопфилда, за исключением самого себя, а также к соответствующим элементам в выходном слое. В режиме функционирования, сеть направляет данные из входного слоя через фиксированные веса соединений к слою Хопфилда. Структурная схема сети Хопфилда представлена на рис. 1. 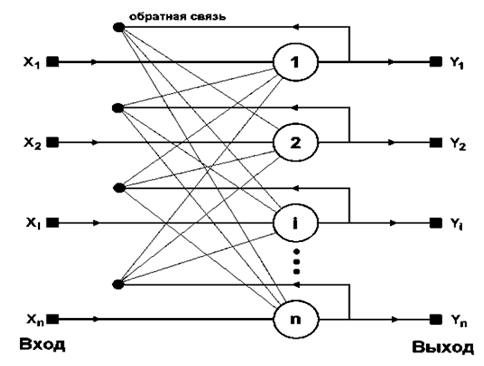 Рис. 1. - Схема сети Хопфилда Сеть Хопфилда состоит из N искусственных нейронов. Граница ёмкости памятидля сети (то есть количество образов, которое она может запомнить) составляет приблизительно 15% от числа нейронов в слое Хопфилда (N*0,15). При этом запоминаемые образы не должны быть сильно коррелированны. Размерности входных и выходных сигналов в сети ограничены при программной реализации только возможностями вычислительной системы, на которой моделируется нейронная сеть, при аппаратной реализации — технологическими возможностями. Размерности входных и выходных сигналов совпадают. Каждый нейрон системы может принимать одно из двух состояний (что аналогично выходу нейрона с пороговой функцией активации): Благодаря своей биполярной природе нейроны сети Хопфилда иногда называют спинами. Взаимодействие спинов сети описывается выражением («энергетической» функцией, которая уменьшается в процессе функционирования сети): 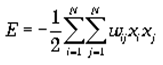 где wij элемент матрицы взаимодействий W, которая состоит из весовых коэффициентов связей между нейронами. В эту матрицу в процессе обучения записывается М «образов» — N-мерных бинарных векторов: Sm = (sm1,sm2,...,smN). В сети Хопфилда матрица связей является симметричной (wij = wji), а диагональные элементы матрицы полагаются равными нулю (wii = 0), что исключает эффект воздействия нейрона на самого себя и является необходимым для сети Хопфилда. Рассмотрим общий алгоритм работы сети:
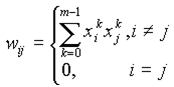 Где i и j ()– индексы, соответственно, предсинаптического (входного) и постсинаптического (выходного) нейронов; wij — i-й синаптический вес j-го нейрона; xik, xjk – i-ый и j-ый элементы вектора k-ого образца.
yj(0) = xj , j = 0...n-1, где yj — аксон (т.е. выход) j-го нейрона. Поэтому обозначение на схеме сети входных синапсов в явном виде носит чисто условный характер. Ноль в скобке справа от yj означает нулевую итерацию в цикле работы сети. 3. Рассчитывается новое состояние нейронов и новые значения аксонов: 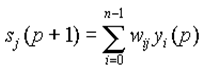 , ,где j=0...n-1, p – номер (конкретный шаг) итерации, - новое состояние нейрона; где f – активационная функция в виде скачка, приведённая на рис. 2б. 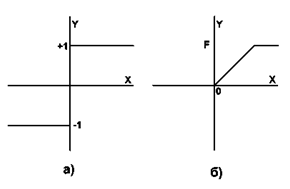 Рис. 2: а) жёсткая пороговая (передаточная)функция сети Хопфилда; б) активационная функция сети Хопфилда. 4. Проверка: изменились ли выходные значения аксонов за последнюю итерацию. Если да – переход к пункту 2, иначе (если выходы застабилизировались) – конец. При этом выходной вектор представляет собой образец, наилучшим образом сочетающийся с входными данными. Алгоритм обучения сети Хопфилда имеет существенные отличия в сравнении с такими классическими алгоритмами обучения перцептронов как метод коррекции ошибки или метод обратного распространения ошибки. Отличие заключается в том, что вместо последовательного приближения к нужному состоянию с вычислением ошибок, все коэффициенты матрицы рассчитываются по одной формуле, за один цикл, после чего сеть сразу готова к работе. Вычисление коэффициентов базируется на следующем правиле: для всех запомненных образов Xi матрица связи должна удовлетворять уравнению: Поскольку именно при этом условии состояния сети Xi будут устойчивы - попав в такое состояние, сеть в нём и останется. Некоторые авторы относят сеть Хопфилда к обучению без учителя. Но это неверно, т.к. обучение без учителя предполагает отсутствие информации о том, к каким классам нужно относить тот или иной образ. Для сети Хопфилда без этой информации нельзя настроить весовые коэффициенты, поэтому здесь можно говорить лишь о том, что такую сеть можно отнести к классу оптимизирующих сетей (фильтров). Отличительной особенностью фильтров является то, что матрица весовых коэффициентов настраивается детерминированным алгоритмом раз и навсегда, и затем весовые коэффициенты больше не изменяются. В сети Хопфилда есть обратные связи и из-за этого нужно решать проблему устойчивости. Веса между нейронами в сети Хопфилда могут рассматриваться в виде матрицы взаимодействий W. Сеть с обратными связями является устойчивой, если её матрица симметрична и имеет нули на главной диагонали. В случае сети Хопфилда условие симметричности является необходимым, но не достаточным, в том смысле, что на достижение устойчивого состояния влияет ещё и режим работы сети. Ниже будет показано, что только асинхронный режим работы сети гарантирует достижение устойчивого состояния сети, в синхронном случае возможно бесконечное переключение между двумя разными состояниями (такая ситуация называется динамическим аттрактором, в то время как устойчивое состояние принято называть статическим аттрактором). Расчёт весовых коэффициентов (обучением сети) происходит по следующей формуле : 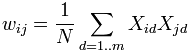 где N - размерность векторов, m – число запоминаемых выходных векторов; d – номер запоминаемого выходного вектора; Xij – i-я компонента запоминаемого выходного j-го вектора. Это выражение может стать более ясным, если заметить, что весовая матрица W может быть найдена вычислением внешнего произведения каждого запоминаемого вектора с самим собой и суммированием матриц, полученных таким образом. Это может быть записано в виде 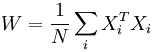 где Xi – i-й запоминаемый вектор-строка. Как только веса заданы, сеть может быть использована для получения запомненного выходного вектора по данному входному вектору, который может быть частично неправильным или неполным. Для этого выходам сети сначала придают значения этого начального вектора. Затем сеть последовательно меняет свои состояния согласно формулам 3-его этапа алгоритма функционирования сети. Полученное устойчивое состояние yj (статический аттрактор), или, возможно, в синхронном случае пара { yj, yj+1 } (динамический аттрактор), является ответом сети на данный входной образ. Существуют 3 режима работы сети Хопфилда: 1) режим фильтрации; 2) синхронный режим; 3) асинхронный режим. Рассмотрим коротко работу сети в режиме фильтрации (восстановление повреждённых образов). Как только веса заданы, сеть может быть использована для получения запомненного выходного вектора по данному входному вектору, который может быть частично неправильным или неполным. Для этого выходам сети сначала придают значения этого начального вектора. Затем сеть последовательно меняет свои состояния согласно формуле нахождения общего алгоритма. Этот процесс называется конвергенцией сети. Это же можно описать так называемым локальным полем ai действующим на нейрон xi со стороны всех остальных нейронов сети: 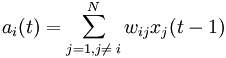 . .После расчёта локального поля нейрона ai(t) это значение используется для расчёта значения выхода через функцию активации, которая в данном случае является пороговой (с нулевым порогом). Соответственно, значение выхода xi(t) нейрона і в текущий момент времени t рассчитывается по формуле: 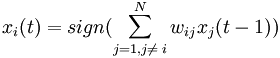 . .Где xj(t ? 1) - значения выходов нейрона j в предыдущий момент времени. Обычно ответом является такое устойчивое состояние, которое совпадает с одним из запомненных при обучении векторов, однако при некоторых условиях (в частности, при слишком большом количестве запомненных образов) результатом работы может стать так называемый ложный аттрактор ("химера"), состоящий из нескольких частей разных запомненных образов, а также в синхронном режиме сеть может прийти к динамическому аттрактору. Обе эти ситуации в общем случае являются нежелательными, поскольку не соответствуют ни одному запомненному вектору - а соответственно, не определяют класс, к которому сеть отнесла входной образ. Рассмотрим коротко работу сети в синхронном режиме работы. Если работа сети моделируется на одном процессоре, то при данном режиме последовательно просматриваются нейроны, однако их состояния запоминаются отдельно и не меняются до тех пор, пока не будут пройдены все нейроны сети. Когда все нейроны просмотрены, их состояния одновременно (т.е. синхронно, отсюда и название) меняются на новые. Таким образом, достигается моделирование параллельной работы последовательным алгоритмом. При реально параллельном моделировании, этот режим фактически означает, что время передачи ?ij для каждой связи между элементами ui и uj одинаковое для каждой связи, что приводит к параллельной работе всех связей, они одновременно меняют свои состояния, основываясь только на предыдущем моменте времени. Наличие таких синхронных тактов, которые можно легко выделить и приводит к пониманию синхронного режима. При синхронном режиме возможно (хотя и далеко не всегда наблюдается) бесконечное чередование двух состояний с разной энергией (динамический аттрактор). Поэтому синхронный режим практически для сети Хопфилда не используется, и рассматривается лишь как основа для понимания более сложного асинхронного режима. Рассмотрим коротко работу сети в асинхронном режиме работы сети. Если моделировать работу сети как последовательный алгоритм, то в данном режиме работы состояния нейронов в следующий момент времени меняются последовательно: вычисляется локальное поле для первого нейрона в момент t, определяется его реакция, и нейрон устанавливается в новое состояние (которое соответствует его выходу в момент t+1), потом вычисляется локальное поле для второго нейрона с учётом нового состояния первого, меняется состояние второго нейрона, и так далее - состояние каждого следующего нейрона вычисляется с учетом всех изменений состояний рассмотренных ранее нейронов. По сути при последовательной реализации сети Хопфилда явно не видно в чём заключается асинхронность, но это видно если сеть Хопфилда реализовать с параллельными вычислениями. В этом случае асинхронный режим сети Хопфилда упрощён, и носит частный случай по сравнению с общим видом асинхронных сетей, где время передачи ?ij для каждой связи между элементами ui и uj свое, но постоянное. Чтобы рассмотреть работу сети при параллельной реализации, необходимо ввести понятие такта - как минимальное время за которое происходит передача сигнала по связи, т.е. при ?ij = 1. Тогда за промежуток времени между t и (t+1) происходит определённое количество тактов N. И именно в пределах времени из N тактов происходит асинхронность протекания сигналов и выполнения расчётов. То есть, например, когда нужно рассчитать состояние нейрона №3 необходимо рассчитать состояния нейрона №1 и состояния нейрона №2 и умножить это на соответствующие веса (рис.1). Но оказывается, для того чтобы рассчитать состояние нейрона №2 нам нужно знать обновленное состояние нейрона №1 и старое состояние нейрона №3, умножить их на соответствующие веса. Понятно, что физически невозможно рассчитать состояние нейрона №1 и состояние нейрона №2 за одно и то же время, т.к. состояние нейрона №2 зависит от состояния нейрона №1. Поэтому связь между нейроном №1 и нейроном №3 имеете время передачи ?ij = 2, и достигает нейрона №3 за два такта. Именное такое разное время передачи ?ij и позволяет говорить о сети Хопфилда как о сети с асинхронным режимом. В асинхронном режиме невозможен динамический аттрактор - вне зависимости от количества запомненных образов и начального состояния, сеть непременно придет к устойчивому состоянию (статическому аттрактору).
Правило обучения для сети Хопфилда опирается на исследования Дональда Хебба (D.Hebb, 1949), который предположил, что синаптическая связь, соединяющая два нейрона будет усиливатьося, если в процессе обучения оба нейрона согласованно испытывают возбуждение либо торможение. Простой алгоритм, реализующий такой механизм обучения, получил название правила Хебба. Рассмотрим его подробно. Пусть задана обучающая выборка образов x a, a = 1..p. Требуется построить процесс получения матрицы связей W, такой, что соответствующая нейронная сеть будет иметь в качестве стационарных состояний образы обучающей выборки (значения порогов нейронов T обычно полагаются равными нулю). В случае одного обучающего образа правило Хебба приводит к требуемой матрице: Покажем, что состояние S=x является стационарным для сети Хопфилда с указанной матрицей. Действительно, для любой пары нейронов i и j энергия их взаимодействия в состоянии x достигает своего минимально возможного значения Eij = -(1/2) x i x j x i x j = -1/2. При этом Е -полная энергия равна E = -(1/2) N 2, что отвечает глобальному минимуму. Для запоминания других образов может применяется итерационный процесс: который приводит к полной матрице связей в форме Хебба:  Устойчивость совокупности образов не столь очевидна, как в случае одного образа. Ряд исследований показывает, что нейронная сеть, обученная по правилу Хебба, может в среднем, при больших размерах сети N, хранить не более чем p » 0.14 N различных образов. Устойчивость может быть показана для совокупности ортогональных образов, когда  В этом случае для каждого состояния x a произведение суммарного входа i-го нейрона hi на величину его активности Si = x ai оказывается положительным, следовательно само состояние xa является состоянием притяжения (устойчивым аттрактором): Таким образом, правило Хебба обеспечивает устойчивость сети Хопфилда на заданном наборе относительно небольшого числа ортогональных образов. В следующем пункте мы остановимся на особенностях памяти полученной нейронной сети.
Сеть Хопфилда Сеть разработана Хопфилдом в 1984 году. С тех пор были предложены многочисленные модификации. Сеть используется как ассоциативная память, классификатор и для решения некоторых задач оптимизации. Одна из первых предложенных моделей сети Хопфилда используется как ассоциативная память. Исходными данными для расчета значений синаптических весов сети являются векторы - образцы классов. Сеть функционирует циклически. Выход каждого из нейронов подается на входы всех остальных нейронов. Нейроны сети имеют жесткие пороговые функции. Итерации сети завершаются после того, как выходные сигналы нейронов перестают меняться. Тип входных и выходных сигналов: биполярные (+1 и -1). Размерности входных и выходных сигналов совпадают. Несколько слов о емкости сети Хопфилда: сеть, содержащая N нейронов может запомнить не более М=0.15 *N образов. При этом запоминаемые образы не должны быть сильно коррелированы. Области применения: ассоциативная память, адресуемая по содержанию, задачи распознавания образов, задачи оптимизации. Сеть обладает небольшой емкостью. Наряду с запомненными образами в сети хранятся и их негативы. Размерность и тип входных сигналов с точностью совпадают с размерностью и типом выходных сигналов. Это существенно ограничивает применение сети в задаче распознавания образов. При использовании коррелированных векторов-образцов возможно зацикливание сети в процессе функционирования. Квадратичный рост числа синапсов при увеличении размерности входного сигнала также можно считать недостатком сети. Сеть имеет огромное историческое значение. С этой модели началось возрождение интереса к нейронным сетям в середине 80-х годов. Существует модель сети Хопфилда с бинарными входными сигналами. Одна из модификаций сети предназначена для решения задач оптимизации, в частности задачи распределения работ между исполнителями. Для увеличения емкости сети и повышения качества распознавания образов используют мультипликативные нейроны. Сети, состоящие из таких нейронов, называются сетями высших порядков. Были предложены многослойные сети Хопфилда, которые обладают определенными преимуществами по сравнению с первоначальной моделью.
Сеть Хопфилда может быть использована как ассоциативная память, для решения некоторых задач оптимизации, а также как фильтр (задачи распознавания образов). Чтобы организовать устойчивую автоассоциативную память с помощью данной сети с обратными связями, веса должны выбираться так, чтобы образовывать энергетические минимумы в нужных вершинах единичного гиперкуба. На каждом итерации алгоритма функционирования сети понижается значение энергии нейронной сети. Это позволяет решать комбинаторные задачи оптимизации, если они могут быть сформулированы как задачи минимизации энергии. Рассмотрим пример восстановления повреждённого изображения. Если во время обучения сформировать матрицу весовых коэффициентов на основании эталонных бинарных векторов, то нейронная сеть в процессе работы будет менять состояния нейронов до тех пор, пока не перейдет к одному из устойчивых состояний. Пусть имеется нейронная сеть размерностью N=100 , в матрицу связей записан набор чёрно-белых картинок (-1 — чёрный цвет, +1 — белый), среди которых есть изображение собачки (рис. 3б). Если установить начальное состояние сети близким к этому вектору (рис. 3а), то в ходе динамики нейронная сеть восстановит исходное изображение (рис. 3б). В этом смысле можно говорить о том, что сеть Хопфилда решает задачу распознавания образов (хотя строго говоря, полученное эталонное изображение ещё нужно превратить в номер класса, что в некоторых случаях может быть весьма вычислительно ёмкой задачей). 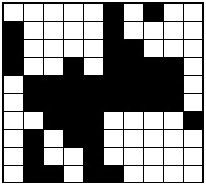 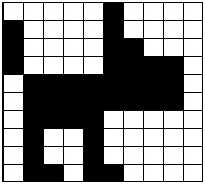 а) б) Рис. 3: а) начальное состояние для сети Хопфилда; б) восстановленное изображение. 4. Достоинства, недостатки и модификации Сети хопфилда Достоинством сети Хопфилда является то, что она имеет огромное историческое значение. С этой модели началось возрождение интереса к нейронным сетям в середине 80-х годов. Также имеющиеся модификации применимы к решению современных задач области применения данной сети. К сожалению, у нейронной сети Хопфилда есть ряд недостатков: 1. Относительно небольшой объём памяти, величину которого можно оценить выражением: Попытка записи большего числа образов приводит к тому, что нейронная сеть перестаёт их распознавать. 2. Достижение устойчивого состояния не гарантирует правильный ответ сети. Это происходит из-за того, что сеть может сойтись к так называемым ложным аттракторам, иногда называемым "химерой" (как правило, химеры склеены из фрагментов различных образов). 3. При использовании коррелированных векторов-образцов возможно зацикливание сети в процессе функционирования. 4. Наряду с запомненными образами в сети хранятся и их негативы. У сети Хопфилда существуют модификации. Одна из них предназначена для решения задач оптимизации, в частности задачи распределения работ между исполнителями. Существует модель сети Хопфилда с бинарными входными сигналами. Для увеличения ёмкости сети и повышения качества распознавания образов используют мультипликативные нейроны. Сети, состоящие из таких нейронов, называются сетями высших порядков. Разработаны к настоящему моменту многослойные сети Хопфилда, которые обладают определёнными преимуществами по сравнению с первоначальной моделью.
Самоорганизующиеся карты могут использоваться для решения задач моделирования, прогнозирования, кластеризации, поиска закономерностей в больших массивах данных, выявления наборов независимых признаков и сжатии информации. Наиболее распространенное применение сетей Кохонена - решение задачи классификации без учителя, т.е. кластеризации. Напомним, что при такой постановке задачи нам дан набор объектов, каждому из которых сопоставлена строка таблицы (вектор значений признаков). Требуется разбить исходное множество на классы, т.е. для каждого объекта найти класс, к которому он принадлежит. В результате получения новой информации о классах возможна коррекция существующих правил классификации объектов. Самым распространенным применением карт Кохонена является: ·разведочный анализ данных ·обнаружение новых явлений В первом случае сеть Кохонена способна распознавать кластеры в данных, а также устанавливать близость классов. Таким образом, пользователь может улучшить свое понимание структуры данных, чтобы затем уточнить нейросетевую модель. Если в данных распознаны классы, то их можно обозначить, после чего сеть сможет решать задачи классификации. Сети Кохонена можно использовать и в тех задачах классификации, где классы уже заданы, - тогда преимущество будет в том, что сеть сможет выявить сходство между различными классами. Во втором случае сеть Кохонена распознает кластеры в обучающих данных и относит все данные к тем или иным кластерам. Если после этого сеть встретится с набором данных, непохожим ни на один из известных образцов, то она не сможет классифицировать такой набор и тем самым выявит его новизну.
Сеть Жордана (Джордана) – это один из видов рекуррентных сетей, которая получается из многослойного персептрона путем введения обратных связей: на вход помимо входного сектора подается выходной с задержкой на один или несколько тактов. Структура этой сети позволяет запоминать последовательности выполняемых действий над объектами, что является важным при решении задачи оптимизации технологических процессов изготовления деталей. Структура сет Д. позволяет учесть «предысторию» выполняемого процесса, накопить информацию для выбора необходимого варианта решения поставленной задач многокритериальной оптимизации перспективного технологического процесса согласно выбранным критериям оптимизации ресурсосбережения (материало, -трудо, -фондо и энергосбережения).  АрхитектурареккурентнойсетиДжордана
Рассмотрим особый класс нейронных сетей, который называется картами самоорганизации. Эти сети основаны на конкурентом обучении. Определение: Самоорганизация – это активное изменение структуры НС или соответствующих ей синоптических весов в результате отклика на обучающие символы. Основой самоорганизации является закономерность, которая состоит в том что глобальное упорядочение глобальной сети возможно в результате самооргранизующих самооперации, которые не зависимо друг от друга проводится в различных локальных сегментах сети. В соответствии с поданными выходными сигналами происходит активация нейронов. Вследствие изменения синоптических весов нейроны адаптируются к поступающим обучающим выборкам. В процессе обучения наблюдается тенденция к росту синоптических весов что приводит к созданию положительной обратной связи: Более мощные возбуждающие стимулы, более высокие значения синоптических весов – большая активность нейронов. В этом случаи происходит естественное расслоение нейронов на различные группы, отдельные нейроны либо их группы сотрудничают между собой, они активируются , в ответ на возбуждение которые создается конкретными обучающими выборками подавляя своей активностью другие нейроны. При этом может быть сотрудничество между нейронами внутри группы так и конкуренция между ними, а так же между различными группами, существует 4 принципа самоорганизации: 1. Изменения синоптических весов ведет к само-усилению НС. 2. Ограниченность ресурсов ведет к конкуренции между синапсами и к успеху более развивающих синапсов за счет других, т.е. наиболее подходящих. 3. Модификация синоптических весов ведет к кооперации. Присутствие сильного синапса может усилить и другие синапсы при общей конкуренции в сети. 4. Порядок и структура образов активации содержит избыточную информацию, которая накапливается сетью в форме знаний являющихся не обходим условием самоорганизующиеся обучения. Данные принципы СО образуют нейробиологический базис для самоорганизующиеся карт кохонина. В картах самоорганизации нейроны помешаются в одно или двухмерной, карты более высокой размерности используются редко. Однако процесс сегментации т.е. сжатие данных большой размерности некоторого набора кластера позволяет визуализировать данные, которые иным способом понять не возможно. Отличительные особенности самоорганизующиеся НС на основе конкуренции. Введенные Кохониным самоорганизующиеся карта признаков(СОК) является НС без обратных связей, которая принципиально отличается от всех типов сетей, сети Кохонена рассчитаны на не управляемое обучение. Они рассчитаны на самостоятельное обучение, во время обучения сообщать им правильные ответы не обязательно. Нейронные сети, обучаемые без учителя служат средством для кластеризации организации и визуального представления больших объемов данных. СОК имеет два слоя: 1. Входной 2. Выходной (составленный обычно из радиальных элементов), так же слой топологической карты. 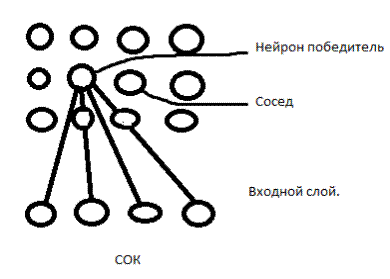 Нейронная сеть обучаемая без учителя. Число нейронов в выходном слое сколько кластеров нейронная сеть может распознать. СОК в отличии от других нейронных сетей не содержит скрытого слоя. Каждый нейрон соединен со всеми компонентами n-мерного входного вектора. Как и в любой нейронной сети, каждой связи свои синоптический вес, в большинстве каждый выходной нейрон соединяется и со своими соседями, эти внутри слойные связи важны в процессе обучения. Поскольку корректировка весов происходит только в окрестности того нейрона, который наилучшем образов откликается на очередной вход. Когда образ предъявляется на образ нейронной сети, каждый нейрон стремится достигнуть наибольшего соответствия с входным образом. Выходной нейрон ближайших к входному образу признается победителем. Синоптические веса нейрона победителя затем корректируются, т.е. сдвигаются в направлении входного образа, это осуществляется с помощью множителя, который определяется темпом или нормой обучения. В этом и состоит сущность СОНС на основе конкуренции. СОК обладает способностью к обобщению – это означает, что подобные нейронные сети могут узнавать или характеризовать входные данные, с которыми они прежде не имеют данные. Новый вектор входных данных соотносится с тем элементом карты, на которой он отображается. Кроме того, для поиска или прогнозирования знание пропущенных данных при применении раннее обученной карты, они могут использовать даже входные векторами с пропущенными данными.
Развитием когнитрона является неокогнитрон, представляющий собой многоуровневую иерархическую нейронную сеть организация и принципы функционирования которой наиболее соответствуют модели зрительной коры головного мозга Неокогнитрон достаточно универсален и находит широкое применение не только для обработки визуальных данных, но и в качестве обобщенной системы распознавания образов Он имеет иерархическую структуру, состоящую из последовательности слоев нейронов (рис 2 15) Входной образ подается на первый слой и передается далее до достижения выходного слоя, в котором он распознается Входной слой неокогнитрона распознает линии и углы определенной ориентации Каждый нейрон в слое, близком к входному, реагирует на определенные образы в определенном месте с определенной ориентацией Каждый последующий слой имеет более абстрактную, менее специфическую реакцию по сравнению с предыдущим В последующих слоях распознаются все более сложные образы независимо от их положения, размера, ориентации и искажений Каждый слой неокогнитрона состоит из двух плоскостей, разделенных на двумерные массивы нейронов Первая плоскость, содержащая простые нейроны, получает сигналы с выходов сложных нейронов предыдущего слоя, выделяет определенные образы и затем передает их во вторую плоскость данного слоя, содержащую сложные нейроны, где образы обрабатываются таким образом, чтобы обеспечить их меньшую позиционную зависимость Внутри отдельного слоя массивы простых и сложных нейронов соответствуют друг другу Рецептивное поле каждого нейрона от слоя к слою возрастает, количество же нейронов в слое при этом уменьшается Наконец, в каждом массиве выходного слоя имеется только один сложный нейрон, который реагирует на определенный входной образ. В процессе распознавания входной образ подается на вход неокогнитрона, а вычисления осуществляются слой за слоем Так как только небольшая часть входного образа подается на вход каждого простого нейрона входного слоя, некоторые простые нейроны реагируют на наличие характеристик, которым они обучены, и возбуждаются В следующих слоях выделяются более сложные характеристики как определенные комбинации выходов сложных нейронов, и уменьшается позиционная зависимость.  Рис. 2.15 Структура неокогнитрона Если используется латеральное торможение, то возбуждается только один нейрон выходного слоя с максимальным значением выхода Однако это часто является не лучшим вариантом Обычно используется подход, при котором будут активизироваться несколько нейронов с различной степенью возбуждения, и входной образ должен быть определен с учетом соотношения их выходов Это позволяет улучшить точность распознавания Простые нейроны. Отдельный массив плоскости простых нейронов настраивается на один специфический входной образ Каждый простой нейрон массива реагирует на ограниченную область входного образа, называемую его рецептивной областью Нейрон реагирует, если часть образа, на которую он настроен, встречается во входном образе и обнаружена в его рецептивной области. Другие массивы простых нейронов первой плоскости в этом слое могут быть настроены, например, на повороты образов Причем для выделения каждого дополнительного образа (или его версии) требуется дополнительная плоскость. Рецептивные области простых нейронов в каждом массиве первой плоскости перекрываются для покрытия всего входного поля этого слоя. Каждый такой нейрон получает сигналы от соответствующих рецептивных областей всех массивов второй плоскости из предыдущего слоя. Следовательно, простой нейрон реагирует на появление своего образа в любой сложной плоскости предыдущего слоя, если он окажется внутри его рецептивной области Простые нейроны неокогнитрона имеют такие же свойства, что и в когнитроне, и для определения их выхода используются те же формулы. Простые нейроны в отличие от сложных имеют настраиваемые веса связей, соединяющих простой нейрон со сложными нейронами в предыдущем слое, настраиваемые таким образом, чтобы выработать максимальную реакцию на определенные образы. Помимо возбуждающих синапсов, к простому нейрону подключены тормозящие, стремящиеся уменьшить значение на его выходе. Сложные нейроны. Сложные нейроны решают задачу уменьшения позиционной зависимости реакции неокогнитрона на образы. Для этого на входы каждого сложного нейрона подаются выходные сигналы с набора простых нейронов из соответствующего множества первой плоскости того же слоя. Активизация любого простого нейрона из рецептивной области сложного нейрона является достаточным условием для возбуждения данного сложного нейрона. Таким образом, сложный нейрон реагирует на тот же образ, что и простые нейроны в соответствующем ему массиве, но он менее чувствителен к позиции образа, чем любой из них. Каждый слой сложных нейронов реагирует на все большую область входного образа, по сравнению с предшествующими слоями, что приводит к требуемому уменьшению позиционной зависимости реакции неокогнитрона на образы в целом. Помимо активизирующих, в плоскости сложных нейронов присутствуют тормозящие нейроны, которые вырабатывают выходные сигналы, пропорциональные квадратному корню из взвешенной суммы квадратов их входных сигналов. При этом на входы тормозящего нейрона подаются сигналы с выходов сложных нейронов из соответствующей рецептивной области для заданного простого нейрона следующего слоя. В символьном виде: где На рис. 2.16 показана организация взаимосвязей между простым нейроном и сложными нейронами из одного из массивов предыдущего слоя. Обучение. Как и для когнитрона, процесс обучения неокогнитрона представляет собой обучение без учителя, в результате которого сеть самоорганизуется. При этом на вход неокогнитрона подается образ, который необходимо распознать, и веса синапсов настраиваются слой за слоем. Значение веса от каждого сложного нейрона к заданному простому увеличивается, когда удовлетворяются следующие два условия: • активизируется сложный нейрон; • реакция одного из простых нейронов больше, чем у его соседей из любой из области конкуренции. Это приводит к тому, что простой нейрон обучается реагировать более сильно на образы, появляющиеся наиболее часто в его рецептивной области. Если распознаваемый образ отсутствует на входе, тормозящий нейрон предохраняет от случайной активизации соответствующий простой нейрон. Процедура обучения и подход при реализации латерального торможения когнитрона и неокогнитрона аналогичны. При этом выходы простых и сложных нейронов являются непрерывными, неотрицательными и изменяются по линейному закону. При срабатывании на входной образ простого нейрона его веса должны быть увеличены. Также увеличиваются веса всех  Рис. 2.16 Взаимосвязь простого нейрона со сложными нейронами из предыдущего слоя простых нейронов из данного массива для этого самого образа. Таким образом, все нейроны в массиве обучаются распознавать одни и те же свойства образа, и после обучения будут делать это независимо от позиции образа в поле сложных нейронов из предшествующего слоя Это определяет способность неокогнитрона к самовосстановлению. Так, если активизируемый нейрон выйдет из строя, среди других выбирается другой, реагирующий наиболее сильно, который и будет обучен распознаванию входного образа, заменяя отказавший нейрон. При обучении с учителем требуемые значения выходов нейронов каждого слоя определяется заранее. Их веса настраиваются с использованием обычных процедур. Например, входной слой настраивался для распознавания отрезков линий в различных ориентациях. Последующие слои обучаются реагировать на более сложные свойства до тех пор, пока в выходном слое требуемый образ не будет выделен.
Уже сегодня искусственные нейронные сети используются во многих областях, но прежде чем их можно будет применять там, где на карту поставлены человеческие жизни или значительные материальные ресурсы, должны быть решены важные вопросы, касающиеся надежности их работы. Поэтому уровень допустимых ошибок следует определять исходя из природы самой задачи. Некоторые проблемы с анализом вопросов надежности возникают из-за допущения полной безошибочности компьютеров, тогда как искусственные нейронные сети могут быть неточны даже при их правильном функционировании. На самом же деле компьютеры, как и люди, тоже могут ошибаться. Первые — в силу различных технических проблем или ошибок в программах, вторые — из-за невнимательности, усталости или непрофессионализма. Следовательно, для особо критических задач необходимо, чтобы эти системы дублировали и страховали друг друга. А это значит, при решении таких задач нейронные сети должны выступать не в качестве единственных средств, а в качестве дополнительных, предупреждающих особые ситуации или берущих на себя управление, когда проблема не решается стандартным образом и какие-либо задержки могут привести к катастрофе. Другая трудность использования нейронных сетей состоит в том, что традиционные нейронные сети неспособны объяснить, каким образом они решают задачу. Внутреннее представление результатов обучения зачастую настолько сложно, что его невозможно проанализировать, за исключением некоторых простейших случаев, обычно не представляющих интереса. В последнее время предпринимаются активные попытки объединения искусственных нейронных сетей и экспертных систем. В такой системе искусственная нейронная сеть может реагировать на большинство относительно простых случаев, а все остальные передаются для рассмотрения экспертной системе. В результате сложные случаи принимаются на более высоком уровне, при этом, возможно, со сбором дополнительных данных или даже с привлечением экспертов. Нейросетевые прикладные пакеты, разрабатываемые рядом компаний, позволяют пользователям работать с разными видами нейронных сетей и с различными способами их обучения. Они могут быть как специализированными (например, для предсказания курса акций), так и достаточно универсальными. Области применения нейронных сетей весьма разнообразны — это распознавание текста и речи, семантический поиск, экспертные системы и системы поддержки принятия решений, предсказание курсов акций, системы безопасности, анализ текстов. Рассмотрим несколько особенно ярких и интересных примеров использования нейронных сетей в разных областях. Необходимо отметить, что мы старались по возможности выбирать наиболее ранние случаи применения нейронных сетей при решении соответствующей задачи. |
