закон гука. Документ Microsoft Word. Понятие о напряжениях и деформации
 Скачать 166.15 Kb. Скачать 166.15 Kb.
|
|
Понятие о напряжениях и деформации Теория упругих волн в горных породах базируется на изучении деформаций и связи их с действующими напряжениями. Деформация (от лат. deformatio – искажение) изменение взаимного расположение точек твердого тела, при котором меняется расстояние между ними, в результате внешних воздействий. Деформация называется упругой, если она исчезает после удаления воздействия, и пластической, если она полостью исчезает. Рассматривая очень маленький объем в упругом теле, различают два основных вида деформаций. В одном случае под действием приложенных сил изменяется объем тела, в то время как его форма (углы между гранями) остается неизменной. Такие деформации называют нормальными деформациями или деформациями объема. В другом случае, наоборот, объем малого параллелепипеда остается неизменным, но его форма (углы между гранями) изменяется. Такие деформации называют деформациями формы или сдвигами. Мерой деформации служат удлинение сторон параллелепипеда, изменение его объема, изменение углов между сторонами. Рассмотрим прямоугольник PQRS в декартовой системе координат. 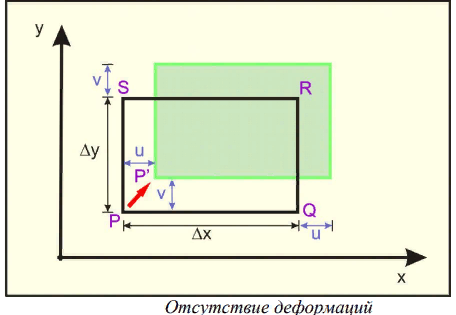 Под действием приложенных сил (напряжений) точка P переместится в положения P’. Смещение по оси x составит u, по оси y – v. Если вершины QRS испытывают такое же смещение, то прямоугольник просто переместится на величины u и v. В этом случае не происходит изменение размеров и формы, а следовательно не происходит деформации. Если смещение различно для разных вершин, то прямоугольник будет испытывать изменение размеров и формы. Таким образом, возникнут деформации. 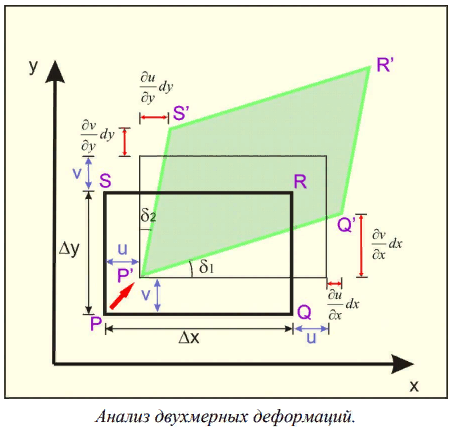 В теории упругости доказывается, что всякую деформацию в упругой среде можно представить всегда как результат наложения происшедших одновременно деформаций — деформаций объема и сдвига. Таким образом, изучение различных сложных видов деформаций может быть сведено к исследованию этих двух основных видов. Деформации определяется как относительные изменения размеров или формы тела. Величины 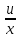 и и 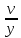 являются относительными увеличениями длины в направлении осей x и y, и их называют нормальными деформациями. являются относительными увеличениями длины в направлении осей x и y, и их называют нормальными деформациями. Нормальные деформации точки P (x,y,z) с компонентами смещения точки в трех измерениях (u, v, w) обозначаются: xx 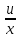 , yy , yy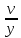 , yy , yy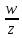 Сумма 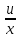 + + 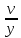 представляет собой величину, на которую уменьшается прямой угол в плоскости xy, т.е. является мерой изменения формы тела и называется сдвиговой деформацией: представляет собой величину, на которую уменьшается прямой угол в плоскости xy, т.е. является мерой изменения формы тела и называется сдвиговой деформацией:xy yx= 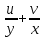 , yz zy= , yz zy=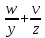 , zx xz= , zx xz=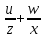 Возникновение деформаций в упругом теле всегда связано с действием внешних или внутренних сил. Предположим, что к упругому телу приложена система внешних сил. Под их действием упругое тело принимает новую форму, т. е. деформируется. Для определения величины силы вне зависимости от размеров тела введено понятие о напряжении. Под напряжением понимают внутреннюю силу, действующую на элементарную площадь в упругом теле, уравновешивающую действие окружающей упругой среды и отнесенную к единице площади. Представим малый элемент объема напряженного тела в виде кубика с ребрами, ориентированными по координатным осям. 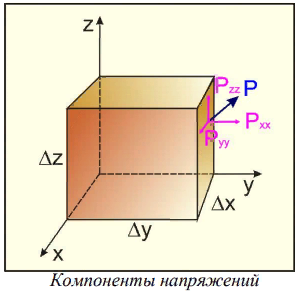 К центру каждой грани кубика приложены произвольные напряжения Р. Эти напряжения раскладываются на нормальные компоненты: Pxx , Pyy , Pzz (взаимно перпендикулярные); и касательные компоненты Pxy=Pyx, Pxz=Pzx, Pyz=Pzy, которые вместе составляют тензор напряжения. Поэтому для определения величины действующих внутренних сил на параллелепипед произвольных размеров, достаточно знать величину нормальных и касательных напряжений. Между напряжениями и деформациями существует связь. Каждая из шести компонент напряжений является линейной функцией шести компонент деформаций. Эта зависимость устанавливается законом Гука, согласно которому величина деформации прямо пропорциональна величине напряжений. Обобщенный закон Гука В основе классической теории упругости лежит обобщенный закон Гука, т. е. предположение о линейной зависимости между прилагаемым к телу напряжением и вызываемой этим напряжением деформацией. Практика показывает, что это предположение оказывается оправданным при малых деформациях и в тех случаях, когда напряжение в среде не превышает предела упругости. Рассмотрим в качестве примера упругий длинный брус круглого сечения, закрепленный торцом на неподвижной опоре. 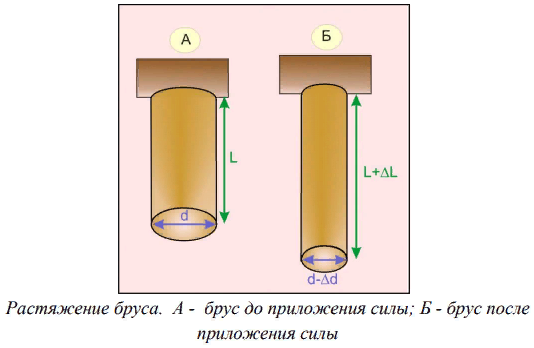 К противоположному торцу бруса приложена сила F. Пусть длина бруса до приложения силы равна l, а диаметр его равен d. Под действием силы F размер и форма бруса изменятся: он удлинится на величину Δl, в то время как диаметр его уменьшится на величину Δd. Согласно закону Гука, между приложенным напряжением и возникающими деформациями должна существовать прямая пропорциональность. Величина напряжения, действующего на единицу площади поперечного сечения бруса 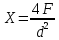 и, следовательно, l aX , d bX Введенные величины a и b зависят не только от свойств вещества, но и от размеров бруса. Чтобы коэффициенты пропорциональности характеризовали только упругие свойства вещества, вводят понятие об относительном удлинении 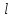 и относительном поперечном сжатии и относительном поперечном сжатии 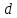 : , : , Подставляя в эти формулы выражения получим 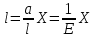 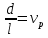 Величина E называется модулем продольного растяжения или модулем Юнга. Модуль Юнга характеризует связь между нормальным напряжением и продольной деформацией в стержне. Другими словами это сопротивление упругого вещества растягивающей (сжимающей) силе. Он численно равен напряжению (силе, действующей на единичную площадь) при котором объемный элемент вещества вдвое растягивается (сжимается). В реальных средах модуль Юнга может различаться в сотни и тысячи раз. Величина 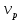 является модулем поперечного сжатия и называется коэффициентом Пуассона. Коэффициент Пуассона это отношение поперечной и продольной деформаций стержня при его продольном растяжении или сжатия. Величина коэффициента Пуассона изменятся от 0 до 0,5. является модулем поперечного сжатия и называется коэффициентом Пуассона. Коэффициент Пуассона это отношение поперечной и продольной деформаций стержня при его продольном растяжении или сжатия. Величина коэффициента Пуассона изменятся от 0 до 0,5. Величины E и 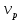 не зависят от размеров и формы тела, а также друг от друга; они характеризуют только упругие свойства вещества. Упругие свойства всякого изотропного упругого тела полностью определены, если известны значения Е и не зависят от размеров и формы тела, а также друг от друга; они характеризуют только упругие свойства вещества. Упругие свойства всякого изотропного упругого тела полностью определены, если известны значения Е и 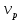 . . В общем случае закон Гука приводит к сложным соотношениям, но если среда изотропна, то ее свойства не зависят от направления. Тогда закон Гука можно выразить в относительно простой форме, используя упругие постоянные Ламе: Pii 2ii , i=x,y,z Pij ij , i, j=x,y,z, i j где Δ=εxx+ εyy+ εzz – относительное изменение объема среды, или дилатация; λ и μ – модули Ламe. Если написать 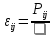 , то ясно, что деформация тем меньше, чем больше модуль μ. Следовательно, μ является мерой сопротивляемости тела действию сдвиговой деформации и называется модулем сдвига. , то ясно, что деформация тем меньше, чем больше модуль μ. Следовательно, μ является мерой сопротивляемости тела действию сдвиговой деформации и называется модулем сдвига. Модуль λ – коэффициент при дилатации в уравнении связи между деформациями сжатия-растяжения и нормальным напряжением. В жидких и газообразных средах, где отсутствуют сдвиговые деформации (μ=0), модуль λ численно равен модулю объемного сжатия K. Модуль всестороннего сжатия характеризует связь между объемной деформацией и величиной равномерного всестороннего давления, т.е. суммой нормальных напряжений. Однако все эти величины связаны между собой и могут быть вычислены, если известны два каких-либо упругих модуля. Закон Гука установлен для абсолютно упругих тел. Он справедлив для большинства горных пород, если деформации и напряжения не слишком велики. Чем меньше величина наблюдаемых деформаций, тем ближе оказывается вещество по своим свойствам к абсолютно упругому телу. Необходимо помнить об ограничении закона Гука. Вблизи области взрыва возникают колоссальные напряжения, и здесь закон Гука неприменим. Лишь для областей, расположенных на некотором удалении от места взрыва, где деформации оказываются достаточно малыми, можно использовать выводы, вытекающие из этого закона. |
