------шпоры_ПССАПР. Понятие проектирования Техническая система
 Скачать 203.32 Kb.
|
|
Экономичность (Вычислительная эффективность) определяется затратами ресурсов, требуемых для реализации модели. Поскольку в САПР используются математические модели, далее речь пойдет о характеристиках именно математических моделей, и экономичность будет характеризоваться затратами машинных времени и памяти. Универсальные модели и методы характеризуются сравнительно большим объемом вычислений, растущим с увеличением размерности задач. Поэтому при решении большинства задач в САПР затраты машинного времени Tм значительны. Обычно именно Tм являются главным ограничивающим фактором при попытках повысить сложность проектируемых на ЭВМ объектов и тщательность их исследования. Поэтому требование экономичности по Tм - одно из основных требований к МО САПР. При использовании в САПР многопроцессорных ВС уменьшить время счета можно с помощью параллельных вычислений. В связи с этим один из показателей экономичности МО - его приспособленность к распараллеливанию вычислительного процесса. В САПР целесообразно иметь библиотеки с наборами моделей и методов, перекрывающими потребности всех пользователей САПР. Затраты памяти являются вторым после затрат машинного времени показателем экономичности МО. Они определяются длиной программы и объемом используемых массивов данных. Несмотря на значительное увеличение емкости оперативной памяти в современных ЭВМ, требование экономичности по затратам памяти остается актуальным. Это связано с тем, что в мультипрограммном режиме функционирования ЭВМ задача с запросом большого объема памяти получает более низкий приоритет и в результате время ее пребывания в системе увеличивается. Улучшить экономичность по затратам оперативной памяти можно путем использования внешней памяти. Однако частые обмены данными между оперативной памятью и внешней могут привести к недопустимому росту Tм. Сущность и история развития математического моделирования Сущность этой методологии состоит в замене исходного объекта его «образом» — математической моделью — и дальнейшем изучении модели с помощью реализуемых на компьютерах вычислительно-логических алгоритмов. Элементы математического моделирования использовались с самого начала появления точных наук. Второе «рождение» этой методологии пришлось на конец 40-х—начало 50-х годов XX века и было обусловлено по крайней мере двумя причинами. Первая из них — появление ЭВМ (компьютеров), хотя и скромных по нынешним меркам, но тем не менее избавивших ученых от огромной по объему рутинной вычислительной работы. Вторая — беспрецедентный социальный заказ — выполнение национальных программ СССР и США по созданию ракетно-ядерного щита, которые не могли быть реализованы традиционными методами. Математическое моделирование справилось с этой задачей: ядерные взрывы и полеты ракет и спутников были предварительно «осуществлены» в недрах ЭВМ с помощью математических моделей и лишь затем претворены на практике. Сейчас математическое моделирование вступает в третий принципиально важный этап своего развития, «встраиваясь» в структуры так называемого информационного общества. Впечатляющий прогресс средств переработки, передачи и хранения информации отвечает мировым тенденциям к усложнению и взаимному проникновению различных сфер человеческой деятельности. Без владения информационными «ресурсами» нельзя и думать о решении все более укрупняющихся и все более разнообразных проблем, стоящих перед мировым сообществом. Однако информация как таковая зачастую мало что дает для анализа и прогноза, для принятия решений и контроля за их исполнением. Нужны надежные способы переработки информационного «сырья» в готовый «продукт», т. е. в точное знание. История методологии математического моделирования убеждает: она может и должна быть интеллектуальным ядром информационных технологий, всего процесса информатизации общества. Технические, экологические, экономические и иные системы, изучаемые современной наукой, больше не поддаются исследованию (в нужной полноте и точности) обычными теоретическими методами. Прямой натурный эксперимент над ними долог, дорог, часто либо опасен, либо попросту невозможен, так как многие из этих систем существуют в «единственном экземпляре». Цена ошибок и просчетов в обращении с ними недопустимо высока. Поэтому математическое (шире — информационное) моделирование является неизбежной составляющей научно-технического прогресса. Этапы математического моделирования Сама постановка вопроса о математическом моделировании какого-либо объекта порождает четкий план действий. Его можно условно разбить на три этапа: модель — алгоритм — программа. На первом этапе выбирается (или строится) «эквивалент» объекта, отражающий в математической форме важнейшие его свойства — законы, которым он подчиняется, связи, присущие составляющим его частям, и т. д. Математическая модель (или ее фрагменты) исследуется теоретическими методами, что позволяет получить важные предварительные знания об объекте. Второй этап — выбор (или разработка) алгоритма для реализации модели на компьютере. Модель представляется в форме, удобной для применения численных методов, определяется последовательность вычислительных и логических операций, которые нужно произвести, чтобы найти искомые величины с заданной точностью. Вычислительные алгоритмы должны не искажать основные свойства модели и, следовательно, исходного объекта, быть экономичными и адаптирующимися к особенностям решаемых задач и используемых компьютеров. На третьем этапе создаются программы, «переводящие» модель и алгоритм на доступный компьютеру язык. К ним также предъявляются требования экономичности и адаптивности. Их можно назвать «электронным» эквивалентом изучаемого объекта, уже пригодным для непосредственного испытания на «экспериментальной установке» — компьютере. 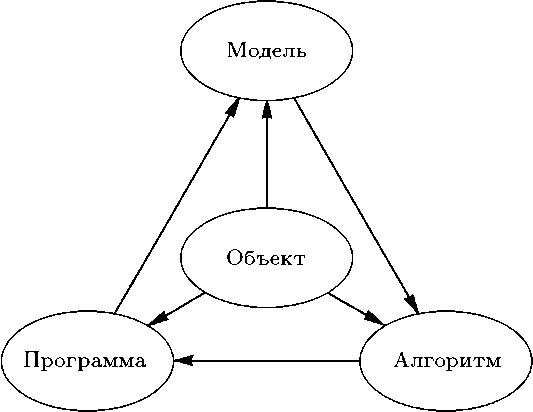 Моделирование присутствует почти во всех видах творческой активности людей различных «специальностей» — исследователей и предпринимателей, политиков и военачальников. Привнесение в эти сферы точного знания помогает ограничить интуитивное умозрительное «моделирование», расширяет поле приложений рациональных методов. Построение математических моделей на основе фундаментальных законов природы Наиболее распространенный метод построения моделей состоит в применении фундаментальных законов природы к конкретной ситуации. Эти законы общепризнаны, многократно подтверждены опытом, служат основой множества научно-технических достижений. Поэтому их обоснованность не вызывает сомнений, что, помимо всего прочего, обеспечивает исследователю мощную психологическую поддержку. На первый план выдвигаются вопросы, связанные с тем, какой закон (законы) следует применять в данном случае и как это делать. Этот закон известен почти двести лет и занимает, пожалуй, наиболее почетное место среди великих законов природы. Полагаясь на него, эксперт по баллистике, желающий быстро определить скорость револьверной пули и не имеющий поблизости специальной лаборатории, может воспользоваться относительно простым устройством типа маятника — груза, подвешенного на легком жестком и свободно вращающемся стержне. Построение математических моделей на основе вариационных принципов Вариационные принципы Они представляют собой весьма общие утверждения о рассматриваемом объекте (системе, явлении) и гласят, что из всех возможных вариантов его поведения (движения, эволюции) выбираются лишь те, которые удовлетворяют определенному условию. Обычно согласно этому условию некоторая связанная с объектом величина достигает экстремального значения при его переходе из одного состояния в другое. Допустим, автомобиль, движущийся с постоянной скоростью v, должен попасть из точки А в точку В и при этом коснуться некоторой прямой линии С (рис. 4). Водитель автомобиля очень торопится и выбирает из множества траекторий путь, требующий минимальных затрат времени. Однако сейчас для нас важно другое — условие минимальных затрат времени привело к выбору соответствующей траектории по правилу «угол падения равен углу отражения». Сформулированные применительно к какому-либо классу явлений вариационные принципы позволяют единообразно строить соответствующие математические модели. Их универсальность выражается также в том, что, используя их, можно в определенной степени отвлекаться от конкретной природы процесса. Так, водитель автомобиля, следующий принципу «минимального времени» и желающий попасть из точки А, находящейся на песчаной почве (одна скорость), в точку Б, расположенную на травянистом лугу (другая скорость), обязан поехать не по прямой, соединяющей А и Б, а по ломанной траектории, сделав необходимое «преломление» на линии, разделяющей песок и траву. Применение аналогий при построении математических моделей В огромном числе случаев при попытке построить модель какого-либо объекта либо невозможно прямо указать фундаментальные законы или вариационные принципы, которым он подчиняется, либо, с точки зрения наших сегодняшних знаний, вообще нет уверенности в существовании подобных законов, допускающих математическую формулировку. Одним из плодотворных подходов к такого рода объектам является использование аналогий с уже изученными явлениями. Что, казалось бы, общего между радиоактивным распадом и динамикой популяций, в частности изменением численности населения нашей планеты? Однако на простейшем уровне такая аналогия вполне просматривается, о чем свидетельствует одна из простейших моделей популяций, называемая моделью Мальтуса. В ее основу положено простое утверждение — скорость изменения населения со временем t пропорциональна его текущей численности N(t), умноженной на сумму коэффициентов рождаемости α(t)≥0 и смертности β(t)≤0. В результате приходим к уравнению 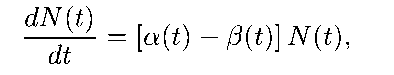 весьма похожему на уравнение радиоактивного распада и совпадающего с ним при α<β (если α и β постоянные). Это неудивительно, так как при их выводе использовались одинаковые соображения. Иерархический подход к получению математических моделей Естествен подход, реализующий принцип «от простого — к сложному», когда следующий шаг делается после достаточно подробного изучения не очень сложной модели. При этом возникает цепочка (иерархия) все более полных моделей, каждая из которых обобщает предыдущие, включая их в качестве частного случая. Построение иерархической цепочки позволило относительно просто прийти к этим важным выводам. Иерархия математических моделей часто строится и по противоположному принципу «от сложного к простому». В этом случае реализуется путь «сверху вниз» — из достаточно общей и сложной модели при соответствующих упрощающих предположениях получается последовательность все более простых (но имеющих уменьшающуюся область применимости) моделей. Нелинейность математических моделей Простота рассмотренных выше моделей во многом связана с их линейностью. В математическом плане это важное понятие означает, что справедлив принцип суперпозиции, т. е. любая линейная комбинация решений (например, их сумма) также является решением задачи. Пользуясь принципом суперпозиции, нетрудно, найдя решение в каком-либо частном случае, построить решение в более общей ситуации. Для нелинейных явлений, математические модели которых не подчиняются принципу суперпозиции, знание о поведении части объекта еще не гарантирует знания поведения всего объекта, а его отклик на изменение условий может качественно зависеть от величины этого изменения. Большинство реальных процессов и соответствующих им математических моделей нелинейны. Линейные же модели отвечают весьма частным случаям и, как правило, служат лишь первым приближением к реальности. Например, популяционные модели сразу становятся нелинейными, если принять во внимание ограниченность доступных популяции ресурсов. При их выводе считается, что: существует «равновесная» численность популяции Np, которую может обеспечить окружающая среда; скорость изменения численности популяции пропорциональна самой численности, умноженной (в отличие от модели Мальтуса) на величину ее отклонения от равновесного значения, т. е. 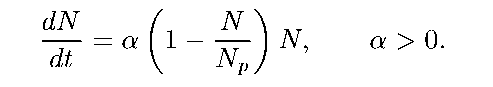 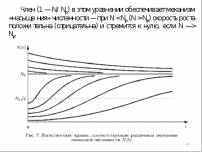 Поведение функции N(t) описывается так называемой логистической кривой (рис. 7). При любом N(0) численность стремится к равновесному значению Np, причем тем медленней, чем величина N(t) ближе к N(0). Тем самым равновесие, в отличие от случая модели (10), устойчиво. Логистическая модель более реалистично отражает динамику популяции в сравнении с моделью Мальтуса, но сама она с необходимостью становится нелинейной и поэтому более сложной. Заметим, что предположения о механизмах насыщения используются при построении многих моделей в различных областях знаний. Этапы создания математической модели Процесс построения моделей может быть условно разбит на следующие этапы. 1. Конструирование модели начинается со словесно-смыслового описания объекта или явления. Помимо сведений общего характера о природе объекта и целях его исследования эта стадия может содержать также некоторые предположения (невесомый стержень, толстый слой вещества, прямолинейное распространение световых лучей и т. д.). Данный этап можно назвать формулировкой предмодели. 2. Следующий этап — завершение идеализации объекта. Отбрасываются все факторы и эффекты, которые представляются не самыми существенными для его поведения. Например, при составлении баланса материи не учитывался, ввиду его малости, дефект масс, которым сопровождается радиоактивный распад. По возможности идеализирующие предположения записываются в математической форме (подобно условию λi >>Li)), с тем чтобы их справедливость поддавалась количественному контролю. 3. После выполнения первых двух этапов можно переходить к выбору или формулировке закона (вариационного принципа, аналогии и т. п.), которому подчиняется объект, и его записи в математической форме. При необходимости используются дополнительные сведения об объекте, также записываемые математически (например, постоянство величины с для всех траекторий лучей света, вытекающее из геометрии задачи). Следует иметь в виду, что даже для простых объектов выбор соответствующего закона отнюдь не тривиальная задача. 4. Завершает формулировку модели ее «оснащение». Например, необходимо задать сведения о начальном состоянии объекта (скорость ракеты и ее массу в момент t = 0) или иные его характеристики (величины I, g; α, λI, λII; α(t) и β(t)), без знания которых невозможно определить поведение объекта. И, наконец, формулируется цель исследования модели (найти закон преломления света, достичь понимания закономерностей изменения популяции, определить требования к конструкции ракеты, запускающей спутник, и т. д.). 5. Построенная модель изучается всеми доступными исследователю методами, в том числе со взаимной проверкой различных подходов. В отличие от рассмотренных простейших случаев, большинство моделей не поддаются чисто теоретическому анализу, и поэтому необходимо широко использовать вычислительные методы. Это обстоятельство особенно важно при изучении нелинейных объектов, так как их качественное поведение заранее, как правило, неизвестно. 6. В результате исследования модели не только достигается поставленная цель, но и должна быть установлена всеми возможными способами (сравнением с практикой, сопоставлением с другими подходами) ее адекватность — соответствие объекту и сформулированным предположениям. Неадекватная модель может дать результат, сколь угодно отличающийся от истинного, и должна быть либо отброшена, либо соответствующим образом модифицирована Современное состояние рынка САПР. Тенденции развития САПР Архитектура и характеристики современных САПР: AutoCAD AutoCAD— 2- и 3-мерная система автоматизированного проектирования и черчения, разработанная компанией Autodesk. AutoCAD является наиболее распространённой САПР в благодаря средствам черчения. Функциональные возможности Ранние версии AutoCAD оперировали элементарными объектами, такими как круги, линии, дуги и др. Однако на современном этапе программа включает в себя полный набор средств, обеспечивающих комплексное трёхмерное моделирование, в том числе работу с произвольными формами, создание и редактирование 3D-моделей тел и поверхностей, улучшенную 3D-навигацию и эффективные средства выпуска рабочей документации. Начиная с версии 2010, в AutoCAD реализована поддержка параметрического черчения, то есть возможность налагать на объект геометрические или размерные зависимости. Средства разработки и адаптации Популярность AutoCAD в мире обусловлена весьма развитыми средствами разработки и адаптации, которые позволяют создавать специализированные приложения, такие как AutoCAD Mechanical, AutoCAD Electrіс. Всего в мире насчитывается более 10000 коммерческих продуктов основанных на AutoCAD. Макрокоманды Макрокоманды (макросы) в AutoCAD являются одним из самых простых средств адаптации, доступных большинству пользователей. Макросы AutoCAD не следует путать с макросами, создаваемыми посредством VBA. |