Понятие схемы Бернулли. Лекция формула Бернулли и наивероятнейшее число успехо.rtf. Понятие схемы Бернулли. Решение задач

• Название: Понятие схемы Бернулли. Решение задач
• Анкор: Понятие схемы Бернулли
• Дата: 07.06.2022
• Размер: 44.2 Kb.
• Имя файла: Лекция формула Бернулли и наивероятнейшее число успехо.rtf.docx
• Тип: Лекция; #575057

Лекция

Тема : Понятие схемы Бернулли. Решение задач.

Цель –

План

1. 
   Формула Бернулли.
   
2. 
   Наивероятнейшее число успехов в схеме Бернулли.
   

1. Формула Бернулли
Формула Бернулли. Схема повторных ис пытаний Бернулли лежит в основе большинства задач по теории

вероятно стей (в том числе и тех, что вы уже решали в первых лекциях.

Здесь мы снова возвращаемся к понятиям случайного опыта, случай ного события и его вероятности.

В явном виде формулируется еще одно важное требование — независимости повторных испытаний.

Для большин ства опытов независимость следует из самой сути явления (бросание мо неты или кубика,

случайный выбор с возвращением и т.д.). В более слож ных экспериментах зависимостью испытаний

приходится просто пренеб регать (например, случайный выбор без возвращения из большой сово купности

объектов).

Испытания Бернулли выделяются из общей схемы повторных неза висимых испытаний тем, что мы

забываем обо всех деталях опыта и фактически разделяем все множество исходов на два класса:

те, что благоприятствуют наступлению некоторого случайного события А (ус пех), и все остальные (неуспех).

С этой точки зрения любые повтор ные независимые испытания можно считать испытаниями Бернулли,

если договориться, какое случайное событие мы будем при этом рассмат ривать в качестве успеха.

Получается, что в каждой схеме повторных независимых испытаний скрыто много разных схем Бернулли:

выбор каждой конкретной из них определяется выбором соответствующего события А.

Таким образом, первое важное умение, которое закладывается в этом разделе, — «увидеть» в опыте

схему Бернулли или убедиться в ее отсут ствии.

Формула Бернулли — одна из первых нетривиальных формул теории вероятностей, доступная для понимания

. Кроме того, она дает ключ к решению многих содержательных задач.

Формула Бернулли в сочетании с другими формулами теории вероят ностей дает возможность вычислить

вероятность сложных событий, воз никающих в схеме Бернулли: вероятность того, что число успехов будет

не больше (не меньше) заданного числа; что она будет лежать в заданном интервале и т.д. Для этого достаточно

просуммировать вероятности со ответствующих исходов, найденные по формуле Бернулли.

Так называемые предельные теоремы в схеме Бернулли позволяют при близить точные значения вероятностей,

которые можно получить по фор муле Бернулли, вероятностями, полученными из других распределений:

нормального и Пуассона.
Если происходит несколько испытаний, причем вероятность события A в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события A.

Пусть производиться n независимых испытаний, в каждом из которых событие A может появиться либо не появиться. Вероятность события в каждом испытании одна и та же, равная p. Вероятность ненаступления события в каждом испытании q = 1 – p.

Вероятность P_n(k) того, что при n испытаниях событие A осуществляется ровно k раз и не осуществляется n – k раз вычисляется по формуле Бернулли:

,

где p^k q^{n - k} – умножение вероятностей независимых событий; – столько можно составить сочетаний из n элементов и k элементов.

Вероятность того, что в n испытаниях событие наступит: а) менее m раз; б) более m раз; в) не менее m раз; г) не более m раз, находят соответственно по формулам:

P_n(0) + P_n(1) +…+ P_n(m – 1);

P_n(m + 1) + P_n(m + 2) +…+ P_n(n);

P_n(m) + P_n(m + 1) +…+ P_n(n);

P_n(0) + P_n(1) +…+ P_n(m).


Пример 1.В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент: а) включено 4 мотора; б) включены все моторы; в) выключены все моторы.

Решение.

1) ;

2) ;

3) .
2.Наивероятнейшее число успехов в схеме Бернулли.

Пусть, как и раньше, P_n(k) есть вероятность того, что событие A наступит ровно k раз в серии из n испытаний Бернулли, и требуется отыскать то число k наступлений события A, которому отвечает наибольшая вероятность P_n(k). Тогда искомыми являются значения k, принадлежащие сегменту [np – q, np + p]. Если при этом число np – q нецелое, то сегмент [np – q, np + p] содержит единственную целочисленную точку k₀, np – q < k₀ < np + p, и для неё P_n(k) < P_n(k₀),

k ≠ k₀. Если np – q – целое, то на сегменте [np – q, np + p] находятся две целочисленных точки

k₁ = np – q и k₂ = np + p; при этом P_n(k₁) = P_n(k₂) и P_n(k) < P_n(k₁) = P_n(k₂), если k отлично от k₁ и k₂.

Отметим, что в литературе часто используется следующая терминология: если в данном опыте (испытании) наступает событие A, то говорят об успехе, в противном случае – о неудаче. С этой точки зрения любая целочисленная точка сегмента [np – q, np + p] является наиболее вероятным (наивероятнейшим) числом успехов в серии из n испытаний Бернулли.

Пример 2. Каково наиболее вероятное число выпадений грани с одной точкой при 26 подбрасываниях игральной кости? Чему равна соответствующая этому числу выпадений вероятность?

Решение. Здесь число n опытов (подбрасываний кости) равно 26, p – вероятность выпадения грани с одной точкой равна 1/6, q =1 – p =5/6. В рассматриваемом случае np – q == = 3,5 – нецелое число, единственное искомое наивероятнейшее число k₀ выпадений грани с одной точкой определяется из условий np – q < k₀ < np + p, в нашем случае 3,5 < k₀ < 4,5, т. е.,

k₀ = 4. (Отметим также, что при нецелом np – q k₀ всегда является ближайшей к числу np – q целочисленной точкой справа). Вероятность P₂₆(4) может быть найдена по формуле Бернулли

.

Пример 3. Вероятность попадания в цель при выстреле из каждого из двух орудий равна 2/3. Залп из двух орудий считается успешным, если хотя бы один снаряд попадёт в цель. Произведено 8 залпов. Каково наиболее вероятное число успешных залпов?

Решение. Вероятность успешного залпа найдём, вычислив предварительно вероятность противоположного события – двух промахов при залпе из двух орудий. Она равна , следовательно, вероятность успешного залпа . Кроме того, число залпов n = 8 и q = 1 – p = . Тогда – целое. Значит, 7 и 8 (8 = np + p) успешных залпов наиболее вероятны (оба случая имеют равную вероятность).

Пример 4. Каким должно быть число подбрасываний игральной кости, чтобы наивероятнейшее число выпадений грани с единицей оказалось равным 5?

Решение. Искомое число подбрасываний n должно быть таким, чтобы значение k = 5 принадлежало сегменту [np – q, np + p]. В рассматриваемом случае , , следовательно, n определяется из неравенств , откуда находим 29 ≤ n ≤ 35.

Отметим, что среди найденных значений n в пяти случаях (n = 30, 31, 32, 33, 34) значение k = 5 является единственным наивероятнейшим числом выпадений грани с единицей (соответствующее np – q – нецелое) и в двух случаях (n = 29, 35) наряду с k = 5 существует другое наиболее вероятное число появлений единицы (np – q – целое).

Пример 5. В семье шесть детей. Вероятность рождения девочки равна 0,49. Найти вероятность того, что среди этих детей одна девочка.

Решение

Событие A – родилась девочка.

P = P(A) = 0,49;

q = 1 – p = 1 – 0,49 = 0,51.

Формула Бернулли:



Всего шесть детей, значит n=6.

Надо найти вероятность того, что среди них точно одна девочка, значит m = 1.




Ответ:
Пример 6. Отрезок AB разделен точной C в отношении 2:1. На этот отрезок наудачу брошено 6 точек. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения. Найти вероятность того, что более одной точки окажется правее точки C.

Решение



Событие A – случайная точка попала на отрезок CB (правее точки C).

Так как C делит AB в отношении 2:1, то:



Значит:

2CB=AC;

2CB+CB=AC+CB;

3CB=AB;



Опираясь на геометрическое определение вероятности, получаем:





Формула Бернулли:



Всего на отрезок AB брошено 6 точек, значит n = 6.

Событие B – более одной точки окажется правее точки C.

Противоположное событие:

– не более одной точки окажется правее точки C, то есть ни одной точки или ровно одна точка.











Ответ:
Пример 7 .Монету бросают 6 раз. Найти вероятность того, что не более 5 раз выпадет герб.

Решение

Событие A – при подбрасывании монеты выпадает герб.



Монета подбрасывается 6 раз, значит n = 6.

Событие B – герб выпадет не более 5 раз.

Противоположное событие: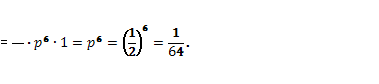

– герб выпадет более 5 раз, то есть 6 раз.







Ответ:
Пример 8. С помощью наблюдений установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность того, что из наугад взятых в этом месяце 8-ми дней 3 будут дождливыми?

Решение:

Поскольку количество испытаний невелико (n = 8), то для нахождения вероятности того, что событие А появится точно k = 3 раза воспользуемся формулой Бернулли:

, где q = 1 – p

По условию задачи вероятность дождя равна p = 12/30 = 6/15, (в сентябре 30 дней).

Значит вероятность ясного дня равна q = 1 – p = 1 – 6/15 = 9/15.

≈ 0,28.
Пример 9. В условиях примера 8 найти вероятность наивероятнейшего числа дней без дождя. (Задача 8. С помощью наблюдений установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность того, что из наугад взятых в этом месяце 8-ми дней 3 будут дождливыми?)

Решение:

Число m₀ называется наивероятнейшим в n независимых испытаниях, если вероятность наступления события А при этом числе наибольшая.

n·p – q ≤ m₀ ≤ n·p + p

По условию задачи 8 вероятность дня без дождя равна p = 9/15, значит вероятность дождливого дня равна q = 6/15. Составим неравенство
17,6 ≤ m₀ ≤ 18,6 ⇒ m₀ = 18

Наивероятнейшее число дней без дождя равно 18.

Пример 10. Вероятность получения удачного результата при проведении сложного химического опыта равна 3/4. Найти вероятность шести удачных результатов в 10-ти опытах.

Решение:

Поскольку количество испытаний невелико (n = 10), то для нахождения вероятности того, что событие А появится точно k = 6 раз воспользуемся формулой Бернулли:

, где q = 1 – p

По условию задачи p = 3/4, значит q = 1 – p = 1 – 3/4 = 1/4.

= ≈ 0,146

Пример 11.Вероятность рождения мальчика равна 0,515, девочки – 0,485. В некоторой семье шестеро детей. Найти вероятность того, что среди низ не больше двух девочек.

Решение:

Пусть событие А состоит в том, что в семье, где шестеро детей, не больше двух девочек, т.е. в указанной семье или одна девочка или две девочки или все мальчики. Поскольку количество испытаний невелико (n = 6), то для нахождения вероятности события А воспользуемся формулой Бернулли:

, где q = 1 – p

По условию задачи вероятность рождения девочки равна p = 0,485 и вероятность рождения мальчика равна q = 0,515, тогда искомая вероятность будет равна

Р(А) = Р₆(0) + Р₆(1) + Р₆(2) = + + =

= 0,018657 + 0,105421 + 0,248201 ≈ 0,37228.
Пример 12. Что вероятнее: выиграть у равносильного противника (включая ничью) три партии из пяти или пять из восьми?

Решение:

Вероятность выиграть у равносильного противника равна p = 0,5, соответственно вероятность проиграть у равносильного противника равна q = 1 – p = 1 – 0,5 = 0,5.

Найдем и сравним такие вероятность Р₅(3) и Р₈(5)

Поскольку количество испытаний невелико (n = 5 и n = 8), то для нахождения вероятности того, что событие А появится точно k = 3 раза (k = 8 раз) воспользуемся формулой Бернулли: , где q = 1 – p

= 10⋅0,03125 = 0,3125;

= 0,2186.

Сравнивая полученные значения вероятностей Р₅(3) = 0,3125 > Р₈(5) = 0,2186 получаем, что вероятнее выиграть у равносильного противника три партии из пяти чем пять из восьми.