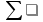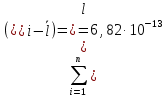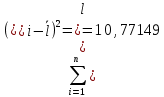Метрология. 3. Границы максимальной неопределенность случайной составляющей погрешности результата наблюдений
 Скачать 242.87 Kb. Скачать 242.87 Kb.
|
|
maЗадача 1. Для определения расстояния до места повреждения кабельной линии связи был использован импульсный рефлектометр. С его помощью получено nрезультатоводнократных измерений (результатов наблюдений) расстояния  до места повреждения. до места повреждения. Считая, что случайная составляющая погрешности рефлектометра распределена по нормальному закону, определить: 1. Результат измерения с многократными наблюдениями расстояния до места повреждения кабеля 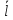 . .2. Оценку среднего квадратического отклонения (СКО) погрешности результата наблюдений (стандартную неопределенность единичного измерения) S; 3. Границы максимальной неопределенность случайной составляющей погрешности результата наблюдений Δмакс; 4. Оценку среднего квадратического отклонения погрешности случайной составляющей результата измерения (стандартную неопределенность результата измерения) 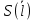 ; ;5. Границы доверительного интервала (расширенную неопределенность) для результата измерения расстояния до места поврежденияεпри заданной доверительной вероятности α ; 6. Записать результат измерения расстояния до места повреждения в соответствии с нормативными документами. 7. Систематическую составляющую погрешности измерения рефлектометра q , если после обнаружения места повреждения было установлено. что действительное расстояние до него составляло  метров. Сравните ее с доверительным интервалом случайной составляющей погрешности результата измерения, и сделать вывод; метров. Сравните ее с доверительным интервалом случайной составляющей погрешности результата измерения, и сделать вывод;8.Предложить способ уменьшения оценки СКО случайной составляющей погрешности результата измерения в D раз. MN = 02 Таблица.1.1 Исходные данные
Таблица 1.2 Исходные данные
Таблица 1.3 Результаты однократных измерений.
Решение Таблица 1.4
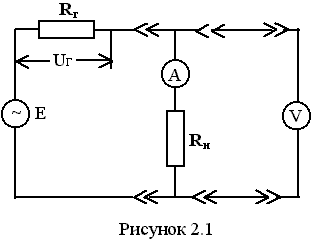
Определим результат измерения с многократными наблюдениями расстояния до места повреждения кабеля. Принимая во внимание то, что истинное значение l измеряемого расстояния неизвестно, вместо значения l возмем наиболее достоверное значение – среднее арифметическое. Получим [2.С.41, ф.(2.10)]: 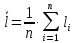 , ,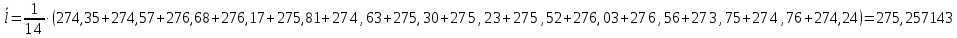 м. м.Зная среднее арифметическое значение, вычислим разность:  , ,где 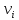 – отлонение результата единичного измерения от среднего – отлонение результата единичного измерения от среднегозначения. Вычислим это отклонение для каждого измерения. Результаты заненсем в табл.1.4. Аналогично занесем в таблицу промежуточные значения для 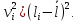 Оценка среднего квадратического отклонения (СКО) погрешности результата наблюдений (стандартную неопределенность единичного измерения) S определяют по формуле[2.С.42, ф.(2.13)]: 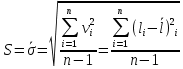 , ,где 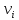 – отклонение результата единичного измерения от среднего значения; – отклонение результата единичного измерения от среднего значения;n – количество результатов наблюдений. 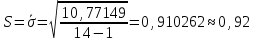 м. м.Вычислим погрешность округления: 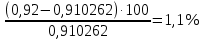 Погрешность округления не превышает 5%, следовательно, округление верное. Максимальная погрешность результата наблюдений Δмакс или предельно допустимая погрешность определяется по формуле: 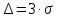 (или (или 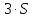 ); [2.С.43] ); [2.С.43]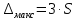 , ,где S – оценка среднего квадратического отклонения (СКО) погрешности результата наблюдений (стандартная неопределенность единичного измерения). 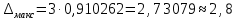 м мВычислим погрешность округления: 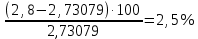 Погрешность округления не превышает 5%, следовательно, округление верное. Вычислим оценку среднего квадратического отклонения (СКО) погрешности случайной составляющей результата измерения (РИ) (стандартную неопределенность результата измерения) 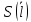 по формуле: по формуле: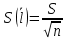 ; ; м мВычислим погрешность округления: 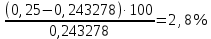 Погрешность округления не превышает 5%, следовательно, округление верное. Произведем расчет границ доверительного интервала (расширенную неопределенность) для результата измерения расстояния до места повреждения ε при заданной доверительной вероятности α. Разчет доверительного интервала осуществляется по формуле: 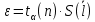 , [3.С.20] , [3.С.20]где  – коэффициент распределения Стьюдента; – коэффициент распределения Стьюдента;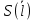 – оценка среднего квадратического отклонения результата измерения – оценка среднего квадратического отклонения результата измеренияИз условия α=0,98, воспользовавшись Приложением II учебника [1] страница 413, получим  = 2,65. = 2,65.Доверительный интервал в этом случае равен 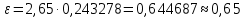 м мВычислим погрешность округления: 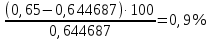 Запишем результат измерения расстояния до места повреждения в соответствии с нормативными документами. Результат измерения согласно МИ 1317-2004:  м, α = 0,98, n= 14, условия измерения нормальные. м, α = 0,98, n= 14, условия измерения нормальные.Определим систематическую составляющую погрешности измерения рефлектометра q. Систематическую погрешность можно найти как отколонени результата измерения 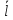 от действительного значения измеряемой физической величины от действительного значения измеряемой физической величины  [3.С.20]: [3.С.20]: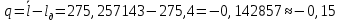 м мВычислим погрешность округления:  Погрешность округления не превышает 5%, следовательно, округление выполнено верно. Сравнивая значения систематической погрешности с границами доверительного интервала ε = 0,65 м, видим, что систематическая погрешность хоть и присутствует, но в разы меньше доверительного интервала, следовательно, расхождение 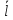 и и  в основном объясняется случайными факторами. в основном объясняется случайными факторами.Рассмотрим способ уменьшения оценки СКО случайной составляющей погрешности результата измерения в D=2,0 раза. Будем считать, что результаты наблюдений распределены по нормальному закону. Точечная оценка дисперсии для результата наблюдений (квадрат СКО результата наблюдений) S2при большом числе наблюдений (в пределе при n→ к бесконечности) стремится к постоянной величине – дисперсии результата наблюдений σ2 [1.С.73]. Известно [1.С.74, ф. (4,24)], что оценка СКО результата измерений зависит от СКО результата наблюдений и числа наблюдений 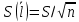 . Из этого выражения видно, что для изменения . Из этого выражения видно, что для изменения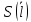 необходимо изменить n. Отсюда можно получить новое число наблюдений, которое позволит уменьшить необходимо изменить n. Отсюда можно получить новое число наблюдений, которое позволит уменьшить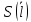 в заданное число D=2,0 раз. в заданное число D=2,0 раз.Основываясь на данных рассуждениях, выведем формулу для определения числа наблюдений, необходимого для уменьшения 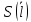 в заданное число D = 2,0 раз: в заданное число D = 2,0 раз: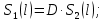 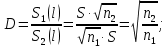 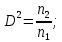 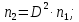 Для изменения 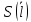 необходимо увеличить число измерений nв D2 = (2,0)2 = 4,0 раза. необходимо увеличить число измерений nв D2 = (2,0)2 = 4,0 раза.Тогда необходимое число измерений будет равно: 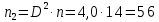 . .Задача 2 При определении вносимого ослабления четырехполюсника необходимо измерить абсолютный уровень мощности рн, отдаваемой генератором с внутренним сопротивлением Rг и ЭДС E в сопротивление нагрузки Rн (рисунок 2.1).
Мощность в нагрузке измеряют с помощью вольтметра V при нормальных условиях измерения. Показания прибора и его метрологические характеристики – условное обозначение класса точности и конечное значение шкалы прибора или диапазона измерения приведены в таблице 2.1. В таблице 2.2 приведены: метрологические характеристики измерительного генератора – числовое значение сопротивления Rг и его относительная погрешность δ Rг; сопротивления нагрузки – значения сопротивления Rни его относительная погрешность δ Rн. MN = 01 Таблица 2.1
Таблица 2.2
Необходимо определить: 1. Абсолютный уровень падения ЭДС генератора рЕ 2. Абсолютный уровень суммарной мощности, выделяемой на внутреннем сопротивлении генератора и сопротивлении нагрузки р∑. 3. Оценить границы абсолютной погрешности измерения абсолютных уровней напряжения и мощности, определенных в п.1 и п.2. 4. Оформить результаты измерения абсолютных уровней напряжения и мощности в соответствии с нормативными документами. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

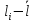 , м
, м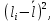 м2
м2