ответы. Понятие системы Система это обособленный пространственно, ограниченный хронально, изменяющийся во времени и относительно самодостаточный фрагмент мира и организованная целостность, состоящая из частей (элементов и др.

• Название: Понятие системы Система это обособленный пространственно, ограниченный хронально, изменяющийся во времени и относительно самодостаточный фрагмент мира и организованная целостность, состоящая из частей (элементов и др.
• Дата: 04.03.2022
• Размер: 380.5 Kb.
• Имя файла: ответы.doc
• Тип: Документы; #382692

1. 
   Понятие системы
   

Система - это обособленный пространственно, ограниченный хронально, изменяющийся во времени и относительно самодостаточный фрагмент мира и организованная целостность, состоящая из частей (элементов и др.), объединенная разного рода отношениями, которая обладает общим особым качеством (эмерджентность), не равным сумме свойств входящих в это целое частей.

2. 
   Моделирование как метод научного познания
   

Моделирование – метод теоретического познания, состоящий в исследовании каких-либо явлений, процессов или систем путем построения и изучения их моделей; использование моделей для определения поведения и характеристик реальных систем.

3. 
   Аналогия. Связь с понятием «система»
   

Аналогия служит одним из источников научных гипотез. греч.Analogia – сходство. Основанием переноса признаков (использование аналогии как метода) в примере явл-ся тот факт, что А и В – системы. Система -сов-ть элементов и связей между ними, которые определяют некоторое новое св-во (интегративное, или системное св-во), присущее совокупности вцелом.

4. 
   Взаимосвязь эксперимента и модели
   

Отношения между экспериментом и моделью могут выразиться: Эксперимент явл источником И. д/моделирования. С другой стороны, модель диктует какой именно эксперимент следует проводить. Модель явл источником эксперимента. Взаимодействие эксперимента и модели заключается в том, что не только опыт явл критерием, но и сама постановка эксперимента диктуется моделью, т.к. вытекает из необходимости ее проверки и уточнения.

5. 
   Черный ящик. Основная проблема моделирования
   

«Черным ящиком» называют систему внутренне содержание которого наблюдателю неизвестна, а доступны только вход и выход. Решением задачи «черным ящиком» называют идентификации системы в широком смысле. Основная задача – определение структуры системы, т.е. определение общего вида матем оператора, связ вход с выходом. 2-я задача – определение синтезов параметров. Это задача определения конкретных решений параметров, связывающий вход с выходом.

6. 
   Классификация видов моделирования.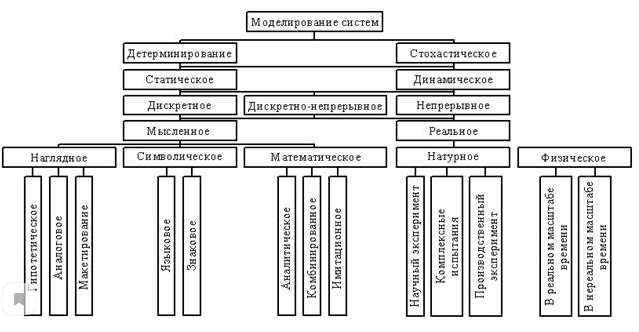
   

7. 
   Виды математического моделирования. Примеры
   

Аналитическое, имитационное и комбинированное. Примером аналитической модели является модель вычисления суммы налоговых поступлений в бюджет за моделируемый период. Примером имитационного моделирования можно считать изобретение крыльев и попытку с их помощью подняться в воздух.

8. 
   Получение случайных чисел с произвольным законом распределения методом обратных функций
   

Метод обратной функции заключается в том, что в качестве независимой переменной F принимаются случайные числа с равномерным законом распределения на интервале [0, 1). Таким образом, для получения последовательности случайных чисел с экспоненциальным законом распределения необходимо взять генератор случайных чисел с равномерным законом распределения (п. 1.1 и 1.2) и преобразовать случайные числа по формуле

9. 
   Получение равномерно распределенных случайных чисел по методу Неймана
   

С помощью датчика случайных чисел получают пару чисел, распределенных равномерно на (0,1).x1 и x2.

Путем преобразований получают два числа , равномерно распределенных соответственно на интервалах (a,b) и (o,w)

Из точек с координатами выбирают те, которые попали “под колокол” функции fh (y)

Если выполнено предыдущее условие, то искомое значение y полагают равным .

10. 
    Получение случайных чисел, подчиняющихся экспоненциальному закону
    

1.Вводятся исходные значения: количество генерируемых величин N (не менее 100) и математическое ожидание экспоненциального закона распределения (THETA);

2.Обнуляется переменная К для подсчета количества генерируемых случайных величин;

3.Генератор псевдослучайных чисел формирует число;

4.Вычисляется случайная величина по формуле 2.7;

5.Значение величины выводится на печать;

6.Значение счётчика случайных величин увеличивается на единицу;

7.Процедура формирования случайных величин повторяется до тех пор, пока не будет получено заданное количество.

11. 
    Моделирование случайных объектов. Квазиравномерное распределение
    

На ЭВМ вместо непрерывной совокупности равномерных случайных чисел интервала [0,1] используют дискретную последовательность 2n случайных чисел того же интервала. Закон распределения такой дискретной последовательности называют квазиравномерным распределением.

12. 
    Методы получения равномерно распределенных случайных чисел
    

Таблицы случайных чисел

Физические генераторы случайных чисел (такие как Firmware Hub или генератор случайных чисел в “ Ivy Bridge ”)

С помощью цифровых генераторов или датчиков, с использованием формул

13. 
    Метод середины квадрата. Общая характеристика, основные недостатки. Требования к функции рекуррентной формулы
    

метод середины квадрата - Первый алгоритмический метод получения равномерно распределенных псевдослучайных чисел, предложил Джон фон Нейман. Суть метода: предыдущее случайное число возводится в квадрат, а затем из результата извлекаются средние цифры. Однако он имеет недостатки:

1. Если какой-нибудь член последовательности окажется равным нулю, то все последующие члены также будут нулями.

2. Последовательности имеют тенденцию "зацикливаться", т. е. в конце концов, образуют цикл, который повторяется бесконечное число раз.

Свойство "зацикливаться" присуще всем последовательностям, построенных по рекуррентной формуле xi+1=f(xi).

Повторяющийся цикл называется периодом. Длина периода у различных последовательностей разная. Чем больше, тем лучше.

14. 
    Общие свойства программных датчиков псевдослучайных чисел
    

большая длинна периода, неотличимость отрезков псевдослучайных чисел от отрезков реализаций независимых случайных величин, имеющих равномерное распределение.

15. 
    Конгруэнтные методы получения равномерно распределенных псевдослучайных чисел
    

Широкое применение для получения последовательностей псевдослучайных равномерно распределенных чисел получили конгруэнтные процедуры генерации, которые могут быть реализованы мультипликативным либо смешанным методом. Конгруэнтные процедуры являются чисто детерминированными, т.к. описываются в виде рекуррентного соотношения.

16. 
    Мультипликативный конгруэнтный метод получения равномерно распределенных псевдослучайных чисел
    

Мультипликативный конгруэнтный метод. Метод представляет собой арифметическую процедуру для генерирования конечной последовательности равномерно распределенных чисел. Основная формула метода имеет вид:



где a и m - неотрицательные целые числа.

17. 
    Смешанный и аддитивный конгруэнтный методы получения равномерно распределенных псевдослучайных чисел.
    

Смешанный метод  базируется на использовании исходной формулы



Мультипликативный метод представляет собой частный случай использования приведенной конгруэнтной процедуры при µ = 0. Соответственно формула принимает вид

18. 
    Программный датчик RANDU. Общая характеристика, принцип работы, особенности
    

RANDU — линейный конгруэнтный генератор псевдослучайных чисел.

Назначение датчика RANDU:

Вычисление равномерно распределенных случайных действительных чисел YF в интервале [0,1] и случайных целых чисел IY в интервале [0,231]. В качестве входа служит целое случайное число IX, на выходе образуется новое целое число IY и вещественное YF.

19. 
    Имитация случайных величин и случайных событий.
    

Имитация случайных событий методом Монте-Карло выполняется следующим образом. Разыгрывается СРРЧ R; если оно оказывается меньшим, чем P (где P — вероятность события), то считается, что смоделировано появление данного события; если R³P, то считается, что смоделировано отсутствие события.

20. 
    Требования к базовому датчику равномерно распределенных чисел. Проверка их соблюдения
    

Отрезок апериодичности, Равномерность, Некоррелированность.

21. 
    Проверка равномерности распределения псевдослучайной последовательности по ее числовым характеристикам
    

Проверка равномерности последовательностей псевдослучайных квазиравномерно распределенных чисел может быть выполнена по гистограмме с использованием косвенных признаков [4, 26]. Суть проверки по гистограмме сводится к следующему. Выдвигается гипотеза о равномерности распределения чисел в интервале Затем интервал разбивается на равных частей, тогда при генерации последовательности каждое из чисел х с вероятностью попадает в один из подынтервалов.

22. 
    Проверка равномерности распределения псевдослучайной последовательности по критериям согласия
    

Мультипликативный конгруэнтный метод. Метод представляет собой арифметическую процедуру для генерирования конечной последовательности равномерно распределенных чисел. Основная формула метода имеет вид:

23. 
    Особенности применения критерия Пирсона при проверке равномерности распределения псевдослучайной последовательности
    

- естественно предположить, что при выборе определенного значения a количество значений c2, удовлетворяющих критерию для данного a, должно составить не менее (1-a)*100 % от общего количества проведенных испытаний. На самом деле этот процент будет несколько ниже;

- если при многократном испытании с использованием критерия Пирсона величина c2 не превысит порогового значения, но каждый раз будет мало отличаться от него, то это свидетельствует о необходимости проведения дополнительных исследований в виду недостаточного согласия гипотетического и эмпирического распределений.

24. 
    Проверка независимости чисел в псевдослучайной последовательности. Критерий автокорреляции.
    

Критерий автокорреляции. Если выборка значений

случайна, то значение каждого ее элемента не должно зависеть от величины предшествующего и последующего членов.

25. 
    Проверка независимости чисел в псевдослучайной последовательности. Критерий разностей
    

Критерий Аббе (критерий квадратов последовательных разностей). Данный критерий служит для выявления наличия систематического смещения значений временного ряда. Здесь для проверки гипотезы (6.8) необходимо вычислить статистику вида. где — несмещенная оценка дисперсии временного ряда х(!)

26. 
    Моделирование случайных чисел с произвольным законом распределения методом отбора
    

метод заключается в построении математической зависимости, связывающей значения случайной величины с заданным законом распределения со значениями случайной величины, распределенной равномерно в интервале (0; 1).

27. 
    Моделирование нормально распределенной случайной величины