Понятия статической и динамической аналитических моделей надежных средств. Понятия статической и динамической аналитических моделей надежностей программного средства

• Название: Понятия статической и динамической аналитических моделей надежностей программного средства
• Анкор: Понятия статической и динамической аналитических моделей надежных средств
• Дата: 16.10.2021
• Размер: 47.43 Kb.
• Имя файла: The concepts of static and dynamic analytical models of robust t.docx
• Тип: Реферат; #248996

Министерство образования и науки РФ

ФГБОУ ВО «Омский государственный технический университет»
Кафедра «Автоматизированные системы обработки информации и управления»

РЕФЕРАТ

на тему «Понятия статической и динамической аналитических моделей надежностей программного средства»

по дисциплине «Измерительные средства аналитики программных систем и технологий»

студента Перелыгина Павла Валерьевича группы ЗИВТ-191

Проверил:

зав. кафедрой, д-р техн. наук, проф.

____________ А.В. Никонов

«___»____________2020 г.

Выполнил студент:

__________П.В. Перелыгин

«___»____________2020 г.

Омск 2020

Содержание

Введение 3

1 Статические модели надежности. 4

1.1 Статическая модель надежности Миллса. 4

1.2 Статическая модель надежности Липова. 5

1.3 Статическая модель надежности Коркорана. 6

1.4 Статическая модель надежности Нельсона. 6

2 Динамические модели надежности. 8

2.1 Динамическая модель Шумана. 8

2.2 Динамическая модель La Padula. 9

2.3 Динамическая модель Джелинского — Моранды. 9

2.4 Динамическая модель Шика — Волвертона. 10

2.5 Динамическая модель Муса. 10

2.6 Модель переходных вероятностей. 11

Заключение 13

Список используемых источников 14

Введение

Изначально следует определить, что такое надежность программного обеспечения. Под надежность ПО понимается его способность безотказно выполнять определенные функции при заданных условиях в течение заданного периода времени с достаточно большой вероятностью. [4]

В настоящее время актуальной является проблема исследования надежности программного обеспечения (ПО). В рамках данной проблемы можно выделить ряд частных задач, таких как:

- определение основных факторов, влияющих на надежность ПО;

- разработка методов оценки надежности ПО;

- разработка методов, обеспечивающих достижение заданного уровня надежности ПО. [4]

В данной работе рассмотрим такие методы оценки надежности, как статической и динамической аналитических моделей надежности.

Статические модели принципиально отличаются от динамических прежде всего тем, что в них появление отказов не связывают со временем появления ошибок в процессе тестирования, а учитывают только зависимость количества ошибок от числа тестовых прогонов (по области ошибок) или зависимость количества ошибок от характеристики входных данных (по области данных). В динамических же моделях поведение ПО (появление отказов) рассматривается во времени. [4]

1 Статические модели надежности.

1.1 Статическая модель надежности Миллса.

Данная модель предполагает необходимость перед началом тестирования искусственно вносить в программу (засорять) некоторое количество известных ошибок. Ошибки вносятся случайным образом и фиксируются в протоколе искусственных ошибок. Специалист, проводящий тестирование, не знает ни количества ошибок, ни характера внесенных ошибок до момента оценки показателей надежности по модели Миллса. Предполагается, что все ошибки (как естественные, так и искусственно внесенные) имеют равную вероятность быть найденными в процессе тестирования.

Тестируя программу в течение некоторого времени, собирается статистика об ошибках. В момент оценки надежности по протоколу искусственных ошибок все ошибки делятся на собственные и искусственные.

Модель надежности Миллса образуется двумя связанными между собой по смыслу соотношениями.

Первое соотношение N = S n/V предсказывает N - первоначальное количество ошибок в программе. В данном соотношении, которое называется формулой Миллса, S - количество искусственно внесенных ошибок, п - число найденных собственных ошибок, V - число обнаруженных к моменту оценки искусственных ошибок. [1]

Второе соотношение используется для установления доверительного уровня прогноза С (вероятности, с которой можно высказать предположение об N). Величина С является мерой доверия к модели. [1]

Если обнаружены все искусственно рассеянные ошибки (V = N) вероятность того, что значение N найдено правильно, можно рассчитать по следующему соотношению: С=S/(S+K+1). [1]

В случае, когда оценка надежности производится до момента обнаружения всех S рассеянных ошибок, величина С рассчитывается по модифицируемой формуле [1]: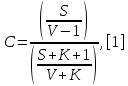



где числитель и знаменатель формулы являются биноминальными коэффициентами вида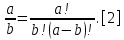



Достоинством модели является простота применения математического аппарата, наглядность и возможность использования в процессе тестирования. Однако модель не лишена и ряда недостатков, самые существенные из которых - это необходимость внесения искусственных ошибок (этот процесс плохо формализуется) и достаточно вольное допущение величины K, которое основывается исключительно на интуиции и опыте человека, проводящего оценку, т.е. допускается большое влияние субъективного фактора.

1.2 Статическая модель надежности Липова.

Липов модифицировал модель Миллса, рассмотрев вероятность обнаружения ошибки при использовании различного числа тестов. Если сделать, то же предположение, что и в модели Миллса, т. е. что собственные и искусственные ошибки имеют равную вероятность быть найденными, то вероятность обнаружения п собственных и V внесенных ошибок составляет [1]:



где т — количество тестов, используемых при тестировании; q — вероятность обнаружения ошибки в каждом из т тестов, рассчитанная по формуле [1]:



S — общее количество искусственно внесенных ошибок; N — количество собственных ошибок, имеющихся в ПС до начала тестирования.

Для использования модели Липова должны выполняться следующие условия [1]:

N ≥ n ≥ 0;

S ≥ V ≥ 0;

M ≥ n + V ≥0.

Модель Липова дополняет модель Миллса, давая возможность оценить вероятность обнаружения определенного количества ошибок к моменту оценки. Использование этой модели предполагает проведение тестирования двумя группами программистов (или двумя программистами в зависимости от величины программы) независимо друг от друга, использующими независимые тестовые наборы. В процессе тестирования каждая из групп фиксирует все найденные ею ошибки. При оценке числа оставшихся в программе ошибок результаты тестирования обеих групп собираются и сравниваются.

1.3 Статическая модель надежности Коркорана.

Модель Коркорана относится к статическим моделям надежности ПС, так как в ней не используются параметры времени тестирования и учитывается только результат N испытаний, в которых выявлено 7V, ошибок i-го типа. Модель использует изменяющиеся вероятности отказов для различных типов ошибок.

В отличие от двух рассмотренных выше статических моделей по модели Коркорана оценивается вероятность безотказного выполнения программы на момент оценки [1]: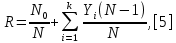



где N₀ — число безотказных выполнений программы; N — общее число прогонов; К — априори известное число типов ошибок;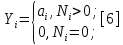



a_i — вероятность выявления при тестировании ошибки i-го типа.

В этой модели вероятность a_i, должна оцениваться на основе априорной информации или данных предшествующего периода функционирования однотипных программных средств.

Наиболее часто встречающиеся ошибки и вероятности их выявлений при тестировании ПС прикладного назначения.

1.4 Статическая модель надежности Нельсона.

Данная модель при расчете надежности ПС учитывает вероятность выбора определенного тестового набора для очередного выполнения программы.

Предполагается, что область данных, необходимых для выполнения тестирования программного средства, разделяется на К взаимоисключающих подобластей Z_i = 1, 2, ..., к. Пусть Р_i — вероятность того, что набор данных Z_i будет выбран для очередного выполнения программы. Предполагая, что к моменту оценки надежности было выполнено N_i прогонов программы на Z_i — наборе данных и из них n_i— количество прогонов закончилось отказом, надежность ПС в этом случае [1]: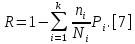

2 Динамические модели надежности.

2.1 Динамическая модель Шумана.

Исходные данные для модели Шумана, которая относится к динамическим моделям дискретного времени, собираются в процессе тестирования ПС в течение фиксированных или случайных временных интервалов. Каждый интервал — это стадия, на которой выполняется последовательность тестов и фиксируется некоторое число ошибок.

Использование модели Шумана предполагает, что тестирование проводится в несколько этапов. Каждый этап представляет собой выполнение программы на полном комплексе разработанных тестовых данных. Выявленные ошибки регистрируются (собирается статистика об ошибках), но не исправляются. По завершении этапа на основе собранных данных о поведении ПС на очередном этапе тестирования может быть использована модель Шумана для расчета количественных показателей надежности. После этого исправляются ошибки, обнаруженные на предыдущем этапе, при необходимости корректируются тестовые наборы и проводится новый этап тестирования. При использовании модели Шумана предполагается, что исходное количество ошибок в программе постоянно и в процессе тестирования может уменьшаться по мере того, как ошибки выявляются и исправляются. Новые ошибки при корректировке не вносятся. Скорость обнаружения ошибок пропорциональна числу оставшихся ошибок. Общее число машинных инструкций в рамках одного этапа тестирования постоянно.

Предполагается, что в начальный момент компоновки программных средств системы в них имеются небольшие ошибки (Е_T– количество ошибок). С этого времени отсчитывается время отладки τ, которое включает затраты времени на выявление ошибок с помощью тестов, на контрольные проверки и т.д. При этом время исправного функционирования системы не учитывается. В течение времени τ устанавливается ε_с (τ) ошибок в расчете на одну команду машинного языка. Удельное число ошибок на одну машинную команду остающихся в системе после времени τ работы равно I_T[1]: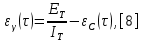



Предполагается, что значение функции частоты отказов Z(t) пропорционально числу ошибок, оставшихся в ПС после израсходованного на тестирование времени τ [1]: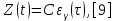



где С — некоторая константа; t — время работы ПС без отказа.

Тогда, если время работы ПС без отказа t отсчитывается от точки I = 0, а τ остается фиксированным, функция надежности, или вероятность безотказной работы на интервале времени от 0 до t [1]: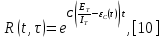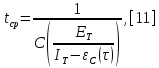





где t_ср - среднее время безотказной работы.

2.2 Динамическая модель La Padula.

По этой модели выполнение последовательности тестов производится в т этапов. Каждый этап заканчивается внесением изменений (исправлений) в ПС. Возрастающая функция надежности базируется на числе ошибок, обнаруженных в ходе каждого тестового прогона.

Надежность ПС в течение i-го этапа [1]: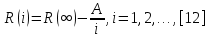



где А – параметр роста; – придельная надежность ПС.

Преимущество модели заключается в том, что она является прогнозной и, основываясь на данных, полученных в ходе тестирования, дает возможность предсказать вероятность безотказной работы программы на последующих этапах ее выполнения.

2.3 Динамическая модель Джелинского — Моранды.

Модель относится к динамическим моделям непрерывного времени. Исходные данные собираются в процессе тестирования ПС. При этом фиксируется время до очередного отказа. Основное положение, на котором базируется модель: значение интервалов времени тестирования между обнаружением двух ошибок имеет экспоненциальное распределение с частотой ошибок (или интенсивностью отказов), пропорциональной числу еще не выявленных ошибок. Каждая обнаруженная ошибка устраняется, число оставшихся ошибок уменьшается на единицу.

Функция плотности распределения времени обнаружения i-й ошибки, отсчитываемого от момента выявления (t_i) i-й ошибки, имеет вид [1]:



где λ_i – частота отказов (интенсивность отказов), которая пропорциональна числу еще не выявленных ошибок в программе [1]:



где N — число ошибок, первоначально присутствующих в программе; С — коэффициент пропорциональности.

Наиболее вероятные значения величин N и С (оценка максимального правдоподобия) можно определить на основе данных, полученных при тестировании. Для этого фиксируют время выполнения программы до очередного отказа t_x, t₂, t₃... .

2.4 Динамическая модель Шика — Волвертона.

Модификация модели Джелинского — Моранды для случая возникновения на рассматриваемом интервале более одной ошибки. Считается, что исправление ошибок производится лишь после истечения интервала времени, на котором они возникли. Частота ошибок (интенсивность обнаружения ошибок) λ_i предполагается постоянной в течение интервала времени и пропорциональна числу ошибок, оставшихся в программе по истечении (i- 1)-го интервала — но она пропорциональна также и суммарному времени, уже затраченному на тестирование Т_i-1 (включая среднее время выполнения программы в текущем интервале) — t_i/2 [1]:

2.5 Динамическая модель Муса.

Модель Муса относят к динамическим моделям непрерывного времени — в процессе тестирования фиксируется время выполнения программы (тестового прогона) до очередного отказа. Но считается, что не всякая ошибка ПС может вызвать отказ, поэтому допускается обнаружение более одной ошибки при выполнении программы до возникновения очередного отказа.

Считается, что на протяжении всего жизненного цикла ПС может произойти M₀ отказов и при этом будут выявлены все N₀ ошибки, которые присутствовали в ПС до начала тестирования.

Общее число отказов M₀ связано с первоначальным числом ошибок N₀ соотношением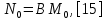



где В – коэффициент уменьшения числа ошибок [1].

В момент, когда проводится оценка надежности, после тестирования, на которое потрачено определенное время t, зафиксировано m отказов и выявлено n ошибок.

Тогда из соотношения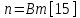



можно определить коэффициент уменьшения числа ошибок В как число, характеризующее количество устраненных ошибок, приходящихся на один отказ [1].

В модели Муса различают два вида времени:

1) суммарное время функционирования 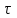, которое учитывает чистое время тестирования до контрольного момента, когда проводится оценка надежности;

2) оперативное время t – время выполнения программы, планируемое от контрольного момента и далее при условии, что дальнейшего устранения ошибок не будет (время безотказной работы в процессе эксплуатации).

Для суммарного времени функционировани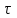я предполагается:

- интенсивность отказов пропорциональна числу неустраненных ошибок;

- скорость изменения числа устраненных ошибок, измеряемая относительно суммарного времени функционирования, пропорциональна интенсивности отказов.

Один из основных показателей надежности, который рассчитывается по модели Муса, – средняя наработка на отказ. Этот показатель определяется как математическое ожидание временного интервала между последовательными отказами и связан с надежностью [1]: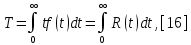



где t – время работы до отказа.

Если интенсивность отказов постоянна (т.е. когда длительность интервалов между последовательными отказами имеет экспоненциальное распределение), то средняя наработка на отказ обратно пропорциональна интенсивности отказов.

2.6 Модель переходных вероятностей.

Эта модель основана на марковском процессе, протекающем в дискретной системе с непрерывным временем.

Процесс, протекающий в системе, называется марковским (или процессом без последствий), если для каждого момента времени вероятность любого состояния системы в будущем зависит только от состояния системы в настоящее время (t₀) и не зависит от того, каким образом система пришла в это состояние. Процесс тестирования ПС рассматривается как марковский процесс.

В начальный момент тестирования (t = 0) в ПС было n ошибок. Предполагается, что в процессе тестирования выявляется по одной ошибке. Тогда последовательность состояний системы (n, n–1, n–2, n–3) и т.д. соответствует периодам времени, когда предыдущая ошибка уже исправлена, а новая еще не обнаружена. Например, в состоянии n–5 пятая ошибка уже исправлена, а шестая еще не обнаружена.

Последовательность состояний {m, m – 1, m – 2, m – 3 и т.д.} соответствует периодам времени, когда ошибки исправляются. Например, в состоянии m – 1 вторая ошибка уже обнаружена, но еще не исправлена. Ошибки обнаруживаются с интенсивностью X, а исправляются с интенсивностью .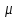

Заключение

Модели надежности программных средств являются одним из средств оценки и повышения надежности ПС. Основным средством определения показателей надежности являются статические и динамические модели надежности.

Модели надежности ПС могут использоваться для расчета показателей надежности (вероятность безотказной работы, вероятность исправления всех ошибок, средняя наработка на отказ), планирования испытаний ПС, выбора стратегии отладки и сроков завершения проекта.

Важным вопросом практического применения моделей является подготовка исходных данных. Эта задача особенно актуальна при моделировании на ранних этапах жизненного цикла. Исходные данные (общее количество ошибок и временные характеристики процессов их поиска и устранения) могут быть получены с использованием объектно – ориентированных метрик сложности и статистики, собранной при разработке похожих программных проектов.

Каждая из вышеприведенных моделей по-своему уникальна и может быть использована для конкретных целей.

Список используемых источников

1. Дубовой, Н. Д. Основы метрологии, стандартизации и сертификации / Н. Д. Дубовой, Е. М. Портнов. – Москва : ИД «ФОРУМ» : ИНФРА-М, 2008. – 255 с

2. Игнатьев, М.Б. Активные методы обеспе­чения надежности алгоритмов и программ / М.Б. Игнатьев, В. В. Фильчаков, Л.Г. Осовецкий. - СПб.: Политехника, 1992.

3. Липаев, В. В. Надежность программных средств/В.В. Липаев.-М.: СИНТЕГ, 1998.

4. Павловская О.О. Статические методы оценки надежности программного обеспечения / О.О. Павловская / Вестник ЮУрГУ. Серия Компьютерные технологии, управление, радиоэлектроника. – 2009. - №10. – С. 35-37.

5. Половко, А. М. Основы теории надежности / А. М. Половко, С.В. Гуров. — 2-е изд., перераб. и доп. - СПб.: ЬХВ-Петербург, 2006.