Лабораторная работа 1. Порядок выполнения работы
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
Лабораторная работа №1 Цель работы: проанализировать факторы, влияющие на устойчивость моделирования на примере анализа адаптивной системы управления. Порядок выполнения работы: 1. Научиться анализировать результаты компьютерного моделирования. 2. Приобрести навыки построения моделей на примере подсистемы моделирования Simulink системы Matlab. 3. Научиться определять влияние структуры алгоритма расчета и иных факторов, влияющих на устойчивость моделирования на примере сравнения неадаптивной и адаптивной систем управления. 4. Выполнить задание согласно своему варианту. 5. Оформить отчет о выполнении работы. Ход работы: Вариант №7. Задание 1. Построить структуру Simulink - модели неадаптивную систему на базе регулятора (6), значений параметров (1) и значений эталонной модели (3), а так же синтезировать Simulink - модель, включающую алгоритм адаптации (8) и подключить его к настраиваемому регулятору (7). Отладку Simulink - модели произвести экспериментально при помощи коэффициента адаптации 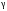 . Провести моделирование системы в условиях скачкообразного трехкратного увеличения параметра . Провести моделирование системы в условиях скачкообразного трехкратного увеличения параметра 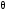 и построить два графика. На одном графике построить x и и построить два графика. На одном графике построить x и  в зависимости от времени, на другом – u в зависимости от времени. в зависимости от времени, на другом – u в зависимости от времени.Таблица 1 – Таблица исходных данных
Имеется технический объект (система), описываемый уравнением вида: 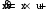 (1) (1)где х – переменная состояния (вектор состояния) объекта; u - сигнал управления (входной вектор управляемых переменных); 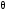 - неизвестный постоянный параметр. - неизвестный постоянный параметр.Эталонная модель описывается передаточной функцией:  (3) (3)где g – сигнал задания;  > 0 – параметр, задающий время переходного процесса. > 0 – параметр, задающий время переходного процесса.Эталонная модель (3) определяет желаемое качество слежения объекта (1) за сигналом задания g. Вычислим производную ошибки слежения ε по времени с учетом (1) и (3): 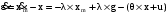 (4) (4)Одна из теорем адаптивных систем доказывает, что ошибка слежения экспоненциально будет стремиться к нулю, если выполняется равенство:  (5) (5)Уравняем правых частей уравнения (4) и уравнения (5) получим: 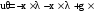 (6) (6)Итак, если известно значение параметра 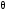 закон управления (6) обеспечивает для объекта (1) выполнение целевого равенства (2). закон управления (6) обеспечивает для объекта (1) выполнение целевого равенства (2).Усложняем задачу, что имеет место в действительности, пусть параметр 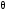 неизвестен. неизвестен.Тогда закон управления (6) также должен соблюдаться, но параметр 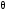 следует заменить на такой же вычисленный (оцениваемый) параметр обозначаемый следует заменить на такой же вычисленный (оцениваемый) параметр обозначаемый 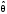 : : (7) (7)Таким образом, необходимо ввести регулятор для нахождения функции 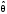 , которая обеспечит устойчивость замкнутой системы и цель управления (2). , которая обеспечит устойчивость замкнутой системы и цель управления (2).Теоретическое обоснование и выбор функции Ляпунова достаточно сложен, приводить его будем. Подчеркнем, что выбор функции Ляпунова позволяет сразу определить устойчивость без решения системы дифференциальных уравнений. При выборе оцениваемого параметра в виде:  (8) (8)Производная функция Ляпунова отрицательная, тем самым обеспечивается устойчивость системы в целом. Алгоритм управления наделяет замкнутую систему следующими свойствами: 1. Устойчивость замкнутой системы и ограниченность всех сигналов; 2. Асимптотическое стремление ошибки  к нулю; к нулю;3. Асимптотическое стремление 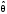 к к 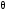 (при ненулевом х); (при ненулевом х);4. Увеличение скорости сходимости параметрической ошибки к нулю при увеличении коэффициента 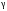 до некоторого оптимального значения. Дальнейшее повышение до некоторого оптимального значения. Дальнейшее повышение 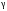 приведет к снижению скорости сходимости ошибки и появлению колебаний в системы. приведет к снижению скорости сходимости ошибки и появлению колебаний в системы.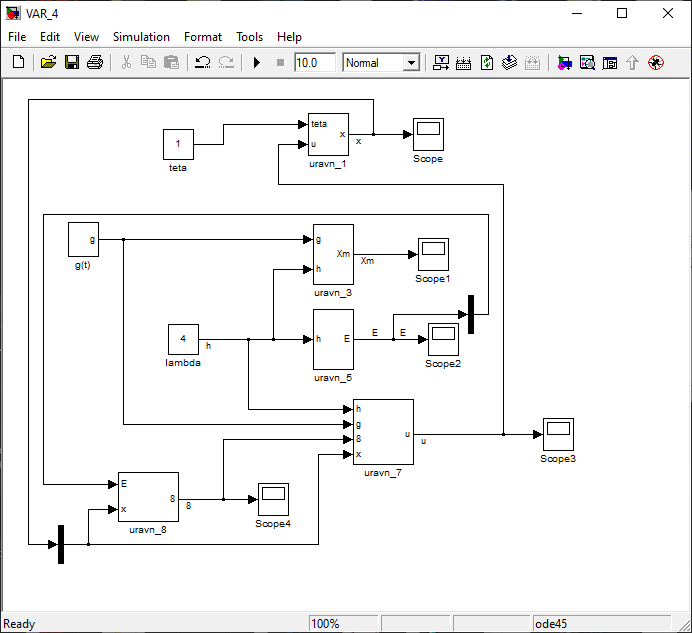 Рисунок 1 – Структура Simulink - модели, решающей систему уравнений.  Рисунок 2 – Блок Simulink соответствующей модели уравнения (1)  Рисунок 3 – Блок Simulink соответствующей модели уравнения (3)  Рисунок 4 – Блок Simulink соответствующей модели уравнения (5)  Рисунок 5 – Блок Simulink соответствующей модели уравнения (7) 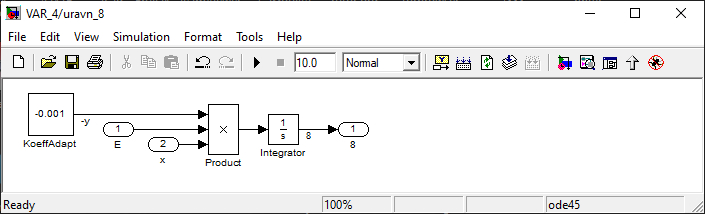 Рисунок 6 – Блок Simulink соответствующей модели уравнения (8)  Рисунок 7 –  в зависимости от времени в зависимости от времени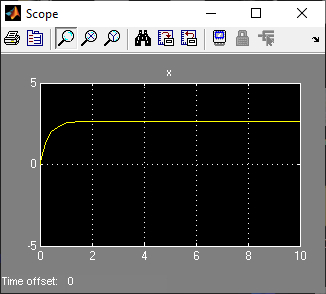 Рисунок 8 – x в зависимости от времени  Рисунок 9 – u в зависимости от времени Вывод: в результате лабораторной работы мы научились анализировать факторы, влияющие на устойчивость моделирования на примере анализа адаптивной системы управления. Лабораторная работа 2 Ответы на вопросы 1. 2. Свойства устойчивости по Ляпунову, асимптотической устойчивости и равномерной асимптотической устойчивости не являются грубыми по отношению к параметрическим возмущениям. Класс линейных стационарных динамических систем допускает наглядную геометрическую интерпретацию введенного понятия грубости свойств устойчивости. 3. Экспоненциальной устойчивости является грубым по отношению к параметрическим возмущениям, так как оно сохраняется хотя бы при малых отклонениях истинных параметров объекта от принятых. 4. Да, порядок роста сложности (или аксиоматическая сложность) описывает приблизительное поведение функции сложности алгоритма при большом размере входа. 5. Установившаяся ошибка зависит от законов изменения и численных характеристик входных сигналов системы. 6. 7. |
