Курсовая по мат.методам. Построение и анализ нелинейных регрессионных моделей в экономике недвижимости
 Скачать 416.74 Kb. Скачать 416.74 Kb.
|
|
Тема: «Построение и анализ нелинейных регрессионных моделей в экономике недвижимости » Содержание Введение…………………………………………………………………………...3 Глава 1Теоретические основы методов построения нелинейных регрессионных моделей…………………………………………………………..5 1.1 Линейная регрессия и виды нелинейных моделей регрессии……………...5 1.2 Линеаризация и логарифмические преобразования………………………...8 1.3 Понятие регрессии и оценка качества модели…………………………….12 Глава 2 Анализ нелинейных регрессионных моделей в экономике недвижимости………………………………….………………………………...17 Заключение……………………………………………………………………….25 Список литературы………………………………………………………………26 Введение В данной курсовой работе рассматриваются нелинейные модели регрессии и анализ нелинейных регрессионных моделей в экономике недвижимости. Цель работы: Изучить методы построения моделей нелинейных процессов. Задачи работы: Ознакомиться с понятиями линейной регрессии и видами нелинейных регрессий; Привести внутренне линейные модели к линейному виду с помощью логарифмирования; Оценить качество полученных моделей и их адекватность; Проанализировать нелинейные регрессионные модели в экономике недвижимости. Предметом исследования выступает выбор наиболее подходящей модели для описания зависимости между исходными данными. Объект исследования – исследование нелинейных моделей регрессии и анализ нелинейных регрессионных моделей в экономике недвижимости. В работе использовались различные методы исследования: эконометрические, экономические, математические, а также использование табличного процессора Microsoft Excel. Курсовая работа состоит из 2-х глав. В первой главе приводятся теоретические и основы методов построения нелинейных регрессионных моделей. Приводятся определения понятий модели, линейной регрессии, рассматриваются основные виды нелинейной регрессии, и приведение их к линейному виду простой заменой переменных и дальнейшая оценка параметров. Наличие формул коэффициента эластичности, индекса корреляции, индекса детерминации и F- критерия Фишера позволяет оценить качество полученных моделей и их адекватность. Во второй главе рассмотрен анализ нелинейных регрессионных моделей в экономике недвижимости. Глава I. Теоретические основы методов построения нелинейных регрессионных моделей Линейная регрессия и виды нелинейных моделей регрессии Математические модели широко применяются в бизнесе, экономике, общественных науках, исследовании экономической активности даже в исследовании политических процессов. Математические модели полезны для более полного понимания сущности происходящих процессов, их анализа. Модель, построенная и верифицированная на основе (уже имеющихся) наблюденных значений объясняющих переменных, может быть использована для прогноза значений зависимой переменной в будущем или для других наборов значений объясняющих переменных. Простейшая модель регрессии – линейная регрессия. Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида 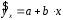 или или  . (1.1) . (1.1)Уравнение вида 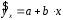 позволяет по заданным значениям фактора позволяет по заданным значениям фактора 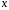 находить теоретические значения результативного признака, подставляя в него фактические значения фактора находить теоретические значения результативного признака, подставляя в него фактические значения фактора 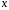 . .Построение линейной регрессии сводится к оценке ее параметров –  и и  . Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров . Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров  и и  , при которых сумма квадратов отклонений фактических значений результативного признака , при которых сумма квадратов отклонений фактических значений результативного признака 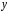 от теоретических от теоретических  минимальна: минимальна: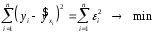 . (1.2) . (1.2)Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. Различают два класса нелинейных регрессий: Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например – полиномы различных степеней – 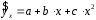 , , . .– равносторонняя гипербола – 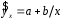 ; ;– полулогарифмическая функция –  . .Регрессии, нелинейные по оцениваемым параметрам, например – степенная – 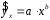 ; ;– показательная – 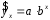 ; ;– экспоненциальная – 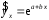 . .Нелинейная регрессия по включенным переменным не имеет никаких сложностей для оценки её параметров. Они определяются, как и в линейной регрессии, методом наименьших квадратов. Параметры a, b и c определяются либо методом подстановки, либо методом определителей.   – определитель системы; – определитель системы;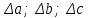 - частные определители для параметров a, b, c. - частные определители для параметров a, b, c. 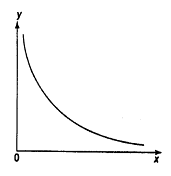  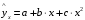 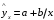 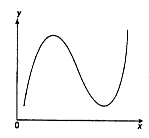 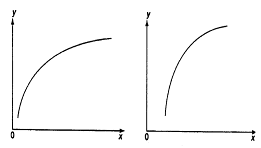 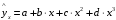 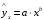 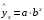 Рис. 1.1 Основные типы кривых, используемые при количественной оценке связей между двумя переменными1.2 Линеаризация и логарифмические преобразования Регрессии нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных (линеаризация), а дальнейшая оценка параметров производится с помощью метода наименьших квадратов. Рассмотрим некоторые функции. Парабола второй степени 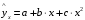 приводится к линейному виду с помощью замены: приводится к линейному виду с помощью замены: 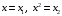 . В результате приходим к двухфакторному уравнению . В результате приходим к двухфакторному уравнению  , оценка параметров которого при помощи МНК, приводит к системе следующих нормальных уравнений: , оценка параметров которого при помощи МНК, приводит к системе следующих нормальных уравнений: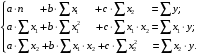 А после обратной замены переменных получим  (1.3) (1.3)Парабола второй степени обычно применяется в случаях, когда для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. Равносторонняя гипербола 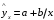 приводится к линейному уравнению простой заменой: приводится к линейному уравнению простой заменой: 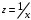 . Система линейных уравнений при применении МНК будет выглядеть следующим образом: . Система линейных уравнений при применении МНК будет выглядеть следующим образом: (1.4) (1.4)Аналогичным образом приводятся к линейному виду зависимости 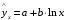 , , 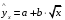 и другие. и другие.Несколько иначе обстоит дело с регрессиями нелинейными по оцениваемым параметрам, которые делятся на два типа: нелинейные модели внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и нелинейные модели внутренне нелинейные (к линейному виду не приводятся). К внутренне линейным моделям относятся - степенная функция – 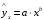 Линеаризация проводится логарифмированием, Сделаем замены: |
| Название функции | Вид модели | Заменяемые переменные | Вид линеаризированной модели |
| Показательная | Ln y = Ln a+ х ln b | Ln y = Y, Ln a = α, Ln b =β | Y = a + xb |
| Степенная | Ln y = Ln a+ b ln x | Ln y = Y, Ln a = α, Ln x =x | Y = a + bx |
| гиперболическая | Y = a + b/x | 1/x=X | Y = a +b X |
Рассмотрим далее функции вида (1.8), которые являются нелинейными как по параметрам, так и по переменным:
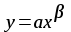 . (1.8)
. (1.8)Мы обнаружим, что соотношение (1.8) может быть преобразовано в линейное уравнение путем использования логарифмов.
Применение логарифмов
Основные правила гласят:
Если у = xz, то log у = log x + log z-
Если у = x/z, то log у = log х – log z.
Если у = хп, то log у – n log х
Эти правила могут применяться вместе для преобразования более сложных выражений. Например, возьмем уравнение (1.8). Если
 то по правилу 1:
то по правилу 1:log у = log а + log x
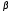 и по правилу 3
и по правилу 3= log a +
 log х.
log х.Для натуральных логарифмов справедливо еще одно правило:
4. Если у = ex, то log у = х.
Выражение ех, которое часто записывается как exp (x), известно также как антилогарифм х. Можно сказать, что log (
 ) является логарифмом антилогарифма х, и так как логарифм и антилогарифм взаимно уничтожаются, неудивительно, что log (е
) является логарифмом антилогарифма х, и так как логарифм и антилогарифм взаимно уничтожаются, неудивительно, что log (е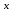 ) превращается просто в х.
) превращается просто в х.Используя приведенные выше правила, уравнение (1.8) можно преобразовать в линейное путем логарифмирования его обеих частей. Если соотношение (4.4) верно, то
logy = log
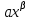 = log a +
= log a +  logx (1.9)
logx (1.9)Если обозначить у’= log у, z = log х и a'= log а, то уравнение (1.8) можно переписать в следующем виде:
у'=а'+βz. (1.10)
Процедура оценивания регрессии теперь будет следующей. Сначала вычислим у' и z для каждого наблюдения путем взятия логарифмов от исходных значений. Вы можете сделать это на компьютере с помощью имеющейся статистической программы. Затем оценим регрессионную зависимость у' от z. Коэффициент при z будет представлять собой непосредственно оценку β. Постоянный член является оценкой а', т. е. log а. Для получения оценки а необходимо взять антилогарифм, т. е. вычислить ехр (а’).
1.3 Понятие регрессии и оценка качества моделей
| |
Парной регрессией называется уравнение связи двух переменных у и х
вида
У=f(x),
где у - зависимая переменная (результативный признак); х - независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессия описывается уравнением: y = a + b ¦ x + є.
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Примеры регрессий, нелинейных по объясняющим переменным, но линейных по оцениваемым параметрам:
полиномы разных степеней у = a + b1 ¦ x + b2 ¦ x2 + b3 ¦ x3 + є;
равносторонняя гипербола ух=a+b+є.
Примеры регрессий, нелинейных по оцениваемым параметрам:
степенная-у=a¦xbє;
показательная-ух=a¦bxє;
экспоненциальная-ух=ea+ьx¦є.
Наиболее часто применяются следующие модели регрессий:
Прямой-ух=a+bx;
гиперболы-ух=a+b/x;
параболы-ух=a+bx+cx2;
показательнойфункции-ух=abx ;
степенная функция - ух = axb и др.
Таблица 1.2 Формулы расчёта коэффициентов эластичности
| Вид функции, 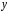 | Первая производная,  | Средний коэффициент эластичности,  |
| 1 | 2 | 3 |
 |  | 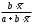 |
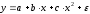 | 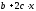 | 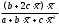 |
 | 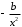 | 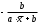 |
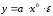 |  |  |
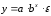 | 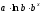 | 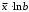 |
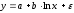 | 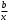 |  |
 |  |  |
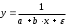 | 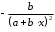 | 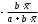 |
В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества регрессионной модели.
Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной
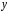 от среднего значения
от среднего значения 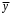 раскладывается на две части – «объясненную» и «необъясненную»:
раскладывается на две части – «объясненную» и «необъясненную»: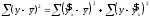 , (1.12)
, (1.12)где
 – общая сумма квадратов отклонений;
– общая сумма квадратов отклонений;  – сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений);
– сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений); 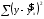 – остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов.
– остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов.Схема дисперсионного анализа имеет вид, представленный в таблице 1.3 (
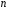 – число наблюдений,
– число наблюдений,  – число параметров при переменной
– число параметров при переменной 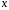 ).
).Табл. 1.3 Схема дисперсионного анализа
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Дисперсия на одну степень свободы |
| Общая |  | 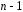 | 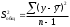 |
| Факторная |  |  | 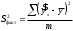 |
| Остаточная |  |  | 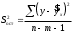 |
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину
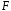 -критерия Фишера:
-критерия Фишера: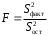 . (1.13)
. (1.13)Фактическое значение
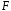 -критерия Фишера сравнивается с табличным значением
-критерия Фишера сравнивается с табличным значением 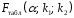 при уровне значимости
при уровне значимости  и степенях свободы
и степенях свободы  и
и  . При этом, если фактическое значение
. При этом, если фактическое значение 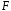 -критерия больше табличного, то признается статистическая значимость уравнения в целом.
-критерия больше табличного, то признается статистическая значимость уравнения в целом.Уравнение нелинейной регрессии, так же, как и в случае линейной зависимости, дополняется показателем тесноты связи. В данном случае это индекс корреляции:
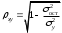 , (1.14)
, (1.14)где
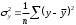 – общая дисперсия результативного признака
– общая дисперсия результативного признака 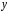 ,
, – остаточная дисперсия.
– остаточная дисперсия.Величина данного показателя находится в пределах:
 . Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.
. Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака
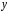 , объясняемую регрессией, в общей дисперсии результативного признака:
, объясняемую регрессией, в общей дисперсии результативного признака: , (1.15)
, (1.15)т.е. имеет тот же смысл, что и в линейной регрессии;
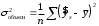 .
.Индекс детерминации
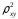 можно сравнивать с коэффициентом детерминации
можно сравнивать с коэффициентом детерминации  для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина
для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина  меньше
меньше 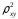 . А близость этих показателей указывает на то, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию.
. А близость этих показателей указывает на то, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию.Индекс детерминации используется для проверки существенности в целом уравнения регрессии по
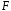 -критерию Фишера:
-критерию Фишера: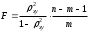 , (1.16)
, (1.16)где
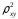 – индекс детерминации,
– индекс детерминации, 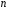 – число наблюдений,
– число наблюдений,  – число параметров при переменной
– число параметров при переменной 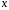 . Фактическое значение
. Фактическое значение 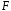 - критерия (1.16) сравнивается с табличным при уровне значимости
- критерия (1.16) сравнивается с табличным при уровне значимости  и числе степеней свободы
и числе степеней свободы  (для остаточной суммы квадратов) и
(для остаточной суммы квадратов) и  (для факторной суммы квадратов).
(для факторной суммы квадратов).О качестве нелинейного уравнения регрессии можно также судить и по средней ошибке аппроксимации, которая вычисляется по формуле:
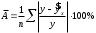 .
. Глава II. Анализ нелинейных регрессионных моделей в экономике недвижимости
Выбор вида уравнения регрессии в оценке недвижимости
ООО "Департамент оценки"
На сегодняшний день все больше оценщиков применяют корреляционно-регрессионный анализ в своих расчетах. Но зачастую выбор регрессионной модели ограничивается простым линейным уравнением.
Если в большинстве случаев оцифровать характеристики объекта оценки и объектов аналогов не представляет труда, то выбор модели (уравнения) регрессии может вызвать сложности у рядовых оценщиков.
Основными этапами регрессионного анализа являются:
Выбор независимых переменных, оказывающих существенное влияние на зависимую переменную.
Оценка параметров уравнения регрессии (параметризация модели).
Выбор вида уравнения регрессии (спецификация модели).
Измерение влияния отдельных факторов на зависимую переменную.
Оценка статистической надежности регрессионной модели (верификация модели).
Выбор формулы связи переменных называется спецификацией уравнения регрессии. В случае парной регрессии выбор формулы обычно осуществляется по графическому изображению реальных статистических данных в виде точек в декартовой системе координат (графический методы выбора уравнения регрессии), которая называется корреляционным полем (или диаграммой рассеивания).
На рис. 1 представлены три ситуации:
а) взаимосвязь между Х и Y близка к линейной, и прямая достаточно хорошо соответствует эмпирическим точкам;
б) реальная взаимосвязь между Х и Y, скорее всего, описывается квадратичной функцией, и какую бы мы ни провели прямую (например, линия 1), отклонения точек наблюдений от нее будут существенными и неслучайными;
в) явная зависимость между Х и Y отсутствует. В данном случае, какую бы мы не выбрали форму связи между переменными, результаты спецификации и параметризации модели будут неудачными.

Рис. 1
Существует и метод перебора различных уравнений, сущность которого заключается в том, что большое число уравнений (моделей) регрессии, отобранных для описания связей какого-либо социально-экономического явления или процесса, реализуется на ЭВМ с помощью специально разработанного алгоритма перебора с последующей статистической проверкой, главным образом на основе t-крнтерия Стьюдeнта и F-критерия Фишера. Способ перебора является достаточно трудоемким и связан с большим объемом вычислительных работ.
Задача определения функциональной зависимости, наилучшим образом описывающей распределение объектов на диаграмме рассеивания, связана с преодолением ряда принципиальных трудностей. В общем случае для стандартизованных данных функциональную зависимость показателя от параметров можно представить в виде
y = f (u1, u2, ...up) + e,
где f – заранее не известная функция, подлежащая определению;
e - ошибка аппроксимации.
Указанное уравнение принято называть выборочным уравнением регрессии y на u. Это уравнение характеризует зависимость между вариацией показателя (стоимость объекта оценки) и вариациями (ценообразующих) факторов. А мера корреляции измеряет долю вариации показателя, которая связана с вариацией факторов. Иначе говоря, корреляцию показателя и факторов нельзя трактовать как связь их уровней, а регрессионный анализ не объясняет роли факторов в создании показателя.
Еще одна особенность касается оценки степени влияния каждого фактора на показатель. Регрессионное уравнение не обеспечивает оценку раздельного влияния каждого фактора на показатель, такая оценка возможна лишь в случае, когда все другие факторы не связаны с изучаемым. Если изучаемый фактор связан с другими, влияющими на показатель, то будет получена смешанная характеристика влияния фактора. Эта характеристика содержит как непосредственное влияние фактора, так и опосредованное влияние, оказанное через связь с другими факторами и их влиянием на показатель.
В регрессионное уравнение не рекомендуется включать факторы, слабо связанные с показателем, но тесно связанные с другими факторами. Не включают в уравнение и факторы, функционально связанные друг с другом (для них в этом случае коэффициент корреляции равен 1). Включение таких факторов приводит к вырождению системы уравнений для оценки коэффициентов регрессии и к неопределенности решения. Поэтому необходимо провести корреляционный анализ ценообразующих факторов.
Функция f должна подбираться так, чтобы ошибка e в некотором смысле была минимальна. Существует бесконечное множество функций, описывающих распределение аналогов абсолютно точно (e = 0), т.е. таких функций, которые для всех значений параметров uj,2 , uj,3 , …, uj,т принимают в точности соответствующие значения показателя yi , i =1, 2, …, п. Вместе с тем, для всех других значений параметров, отсутствующих в результатах наблюдений, значения показателя могут принимать любые значения. Понятно, что такие функции не соответствуют действительной связи между параметрами и показателем.
В целях выбора функциональной связи заранее выдвигают гипотезу о том, к какому классу может принадлежать функция f, а затем подбирают "лучшую" функцию в этом классе. Выбранный класс функций должен обладать некоторой "гладкостью", т.е. "небольшие" изменения значений аргументов должны вызывать "небольшие" изменения значений функции.
Простым, удобным для практического применения и отвечающим указанному условию является класс полиномиальных функций
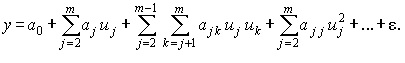
Для такого класса задача выбора функции сводится к задаче выбора значений коэффициентов a0 , aj , ajk , …, ajj , … . Однако универсальность полиномиального представления обеспечивается только при возможности неограниченного увеличения степени полинома, что не всегда допустимо на практике, поэтому приходится применять и другие виды функций.
Частным случаем, широко применяемым на практике, является полином первой степени или уравнение линейной регрессии
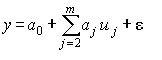 .
.Это уравнение в регрессионном анализе следует трактовать как векторное, ибо речь идет о матрице данных
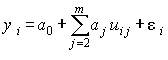 , i =1, 2, … , n.
, i =1, 2, … , n.Обычно стремятся обеспечить такое количество наблюдений, которое превышало бы количество оцениваемых коэффициентов модели. Для нелинейной регрессии при п > т количество уравнений превышает количество подлежащих определению коэффициентов полинома. Но и в этом случае нельзя подобрать коэффициенты таким образом, чтобы ошибка в каждом скалярном уравнении обращалась в ноль, так как к неизвестным относятся аj и ei , их количество n + т – 1, т.е. всегда больше количества уравнений п. Аналогичные рассуждения справедливы и для полиномов степени, выше первой.
На мой взгляд, использование линейного уравнения регрессии применительно к определению стоимости объекта недвижимости возможно только в том случае, если объекты-аналоги расположены в одном ценовом диапазоне (тогда и можно говорить о внутренней линейности нелинейной функции). На рис. 2 приведен пример ценовых диапазонов – А, Б, В.

Рис. 2
При расширении выборки объектов-аналогов – увеличения количества самих аналогов, расширения ценовых сегментов, можно рекомендовать оценщикам к применению нелинейную модель регрессии (например, полиномиальную или степенную).
Это можно объяснить тем, что, к примеру, увеличение на удельную единицу качества объекта на отрезке Х{0.8;1.0} (см. рис. 2) не подразумевает соразмерного увеличения удельной стоимости Y, т.к. зачастую ценообразование высоких классов недвижимости, носит не рыночных характер, а потребительский, и зависит зачастую от желания продавца «снять сливки». Если представить данную ситуацию графически, то получим тренд «A», представленный на рис. 3.
Также среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция у=ахbε. Связано это с тем, что параметр b в ней имеет четкое экономическое истолкование, т.е. он является коэффициентом эластичности. Это означает, что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. По сути, распределение объектов на диаграмме рассеивания представляет собой график предложения на микроуровне, который также подвержен эластичности.

Рис. 3
В общем, для выбора вида функциональной зависимости можно рекомендовать следующий подход:
в пространстве параметров графически отображают точки со значениями показателя. При большом количестве параметров можно строить точки применительно к каждому из них, получая двумерные распределения значений;
по расположению точек и на основе анализа сущности взаимосвязи показателя и параметров объекта делают заключение о примерном виде регрессии или ее возможных вариантах;
после расчета параметров оценивают качество аппроксимации, т.е. оценивают степень близости расчетных и фактических значений;
если расчетные и фактические значения близки во всей области задания, то задачу регрессионного анализа можно считать решенной. В противном случае можно попытаться выбрать другой вид полинома или другую аналитическую функцию, например периодическую.
Хочется заметить, что в экономике, по существу, не бывает линейных связей, это относится и к рынку недвижимости. Нелинейные модели, зачастую могут более корректно отобразить зависимость между ценообразующими факторами от стоимости объекта, но построение таких моделей и, главное, проверка их на значимость требуют от оценщика значительных усилий и специфических знаний в области статистики и эконометрики.
Заключение
нелинейный регрессия инфляция безработный
В первой главе мы рассмотрели теоретические аспекты, а именно что такое модель, линейная регрессия, нелинейная регрессия, какие виды нелинейной регрессии бывают, нахождение параметров, что такое линеаризация, приведение нелинейной функции к линейному виду с помощью замены переменных и логарифмирования. Рассмотрели оценку качества моделей с помощью коэффициентов эластичности, индексов корреляции и оценку адекватности моделей с помощью F – критерия Фишера, привели табличные значения, по которым сравнивается адекватность модели.
Во второй главе мы провели анализ выбора вида уравнения регрессии в оценке недвижимости.Были исследованы следующие функции: линейная,нелинейная, параболическая, гиперболическая и степенная. Путем расчетов мы выяснили, что наилучшим образом из всех рассмотренных функциональных моделей нелинейные модели, зачастую могут более корректно отобразить зависимость между ценообразующими факторами от стоимости объекта.
Список литературы
Магнус Я.Р., Катышев П.К, Пересецкий А.А.. Эконометрика. Начальный курс. Учебное пособие, 6-е издание. М: Дело, 2004 – 576с.
Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002. – 344 с.
Доугерти К. Введение в эконометрику: Пер. с англ. – М.: Инфра-М, 1999, 402 с.
Шалабанов А.К. Эконометрика. Учебно-методическое пособие. Казань, Академия управления «ТИСБИ»,2004.
Трофимов В.В., Тужилин А.А. Математические модели экономики. М.: 2005
Нарбут М.А., Соколовская М.В. Эконометрика: текст лекций/ СПб ГУАП. СПб, 2004. 48 с.
Айвазян С.А., Мхиторян В.С. Прикладная статистика и основы эконометрики: Учебник для ВУЗов. – М.: ЮНИТИ, 1998.
Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для ВУЗов/ Под ред. Проф. Н.Ш.Кремера. – М.: ЮНИТИ-ДАНА, 2002. – 311с.
Статистический ежегодник. 2008 г.
Замков О.О., Черемных Ю.А., Толстопятенко А.В. Математические методы в экономике. Учебник, М..: МГУ им. Ломоносова. Изд. «Дело и Сервис», 1999.
Груббер Й. Эконометрика. В 2-х т. Т 1.: Введение в эконометрию. К., 1996 – 397 с.
Бородич С.А. Вводный курс эконометрики: учебное пособие – Мн.: БГУ, 2000. – 354 с.
Фестер Э., Ренц Б. Методы корреляционного и регрессионного анализа: Пер. с нем. – М.: Финансы и статистика, 1982
Кулинич Е.И. Эконометрия. – М.: Финансы и статистика, 2001. – 304 с.
Эконометрика: Учебн. пособие для вузов / А.И. Орлов – М.: Издательство «Экзамен», 2002. – 576 с.

 (1.5)
(1.5)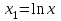 ;
;  ;
; 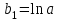 .
. 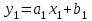 ;
; .
.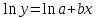 (1.6)
(1.6)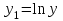 ;
; 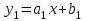 .
. будут найдены, вернуться назад к коэффициентам
будут найдены, вернуться назад к коэффициентам 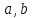 .;
.; ,
,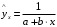 .
.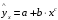 ,
, 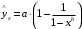 .
.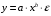 , которая приводится к линейному виду логарифмированием:
, которая приводится к линейному виду логарифмированием: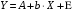 , (1.7)
, (1.7)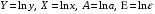 . Т.е. МНК мы применяем для преобразованных данных:
. Т.е. МНК мы применяем для преобразованных данных: