Главная страница
Навигация по странице:

  • Развивающие

  • Тип урока

  • Изучение нового материала.

  • Мы составили алгоритм решения системы методом подстановки. Формирование умений и навыков.

    		•

    карточки. Решение систем линейных уравнений методом подстановки


    Скачать 202.21 Kb.
    НазваниеРешение систем линейных уравнений методом подстановки
    Анкоркарточки
    Дата10.05.2022
    Размер202.21 Kb.
    Формат файлаdocx
    Имя файла00027ac8-cd29fc56.docx
    ТипКонспект
    #520743

    План – конспект урока по алгебре в 7-м классе на тему:

    «Решение систем линейных уравнений методом подстановки»

    Цели урока:

    Образовательные: – разобрать, в чем состоит метод подстановки решения систем линейных уравнений; вывести алгоритм применения этого метода; сформировать умение решать системы уравнений методом подстановки.

    Воспитательные: – воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.

    Развивающие: - развитие зрительной памяти, математически грамотной речи, логического мышления, сознательного восприятия учебного материала.

    Задачи:

    1.Предметные: разобрать, в чем состоит метод подстановки решения систем линейных уравнений; вывести алгоритм применения этого метода; сформировать умение решать системы уравнений методом подстановки продолжить формирование мотивации обучающихся к изучению предмета.

    2.Метапредметные: развивать операционный стиль мышления, способствовать приобретению учащимися навыков общения при совместной работе, активизировать их творческое мышление; продолжить формирование определенных компетенций обучающихся, которые будут способствовать их эффективной социализации, навыков самообразования и самовоспитания

    3.Личностные: воспитывать культуру, способствовать формированию личностных качеств, направленных на доброжелательное, толерантное отношение к людям, жизни; воспитывать инициативу и самостоятельность в деятельности; подвести к пониманию необходимости изучаемой темы для успешной подготовки к государственной итоговой аттестации.

    Тип урока: урок изучения новой темы.

    Вид урока: комбинированный.

    Оборудование: мультимедийный проектор, компьютер.

    Ход урока.

    Актуализация знаний

    Запись даты и темы урока.

    Напомнить учащимся, что на предыдущих уроках мы учились решать системы линейных уравнений.

    Предложить вспомнить:

    • Что такое система двух линейных уравнений с двумя переменными? (Математическая модель, состоящая из двух линейных уравнений с двумя переменными)

    • Что мы называем решением системы уравнений? (Пара чисел (х;у), которая одновременно является решением первого и второго уравнений системы)

    • Какими способами мы умеем решать системы уравнений? (Метод подбора и графический метод)

    Проверка домашнего задания (работа в парах)

    Для повторения предлагаю вам выполнить следующие задания:

    1. Раскрыть скобки (устно с повторением правил раскрытия скобок)

    2(3x – y)

    – 3(2a – 3)

    2x – 3(x + y)

    a – (a – b)

    2. Выразить из уравнения одну переменную через другую. (задание выполняется на доске с комментариями)

    3a + b = 12

    c – 8d = 15

    18m + n = 3

    – p – 9q = 4

    7x – y = 17

    2n – 4k = – 6

    Вопрос: Какую переменную легче выразить через другую в каждом из уравнений и почему?

    3. Является ли пара чисел (2;3) решением системы уравнений: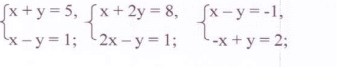



    4.Сколько решений имеет система уравнений: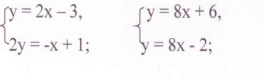



    Изучение нового материала.

    Системы уравнений с двумя переменными, которые имеют одни и те же решения или не имеют решений, называются равносильными.



    Эти системы равносильны, т. к. имеют одно и то же решение (2;1). (проверить устно, подставив в каждую из систем)



    Эти системы равносильны, т. к. каждая из них не имеет решений. (проверить устно)

    При решении системы уравнений с помощью преобразований ее заменяют более простой равносильной системой. Одним из способов решения системы является способ методом подстановки. Давайте решим систему уравнений, составляя таблицу.



    Решим методом подстановки

    1. Выражаем. Из любого уравнения выражаем одну переменную.
    1. Выражаем

    Видно, что во втором уравнении имеется переменная x с коэффициентом 1, отсюда получается, что легче всего выразить переменную x из второго уравнения.

    x=3+10y

    2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.
    2.После того как выразили х через у, подставляем в первое уравнение «3+10y» вместо переменной « x».

    2(3+10y) +5y=1

    3. Решаем полученное уравнение с одной переменной.

    4. Находим вторую переменную.
    3.Решаем полученное уравнение.

    2(3+10y) +5y=1 (раскрываем скобки)

    6+20y+5y=1

    25y= 1-6

    25y= -5

    y= -5:25

    y= - 0,2

    Подставить найденное значение у в выражение х через у.

    x=3+10y

    x=3+10*(-0,2)=1

    4. Записываем ответ: х=…; у=…
    Точки принято записывать на первом месте пишем переменную x, а на втором переменную y.

    Ответ: (1; -0,2) или х=1 и у=-0,2



    Необходимо обратить внимание учащихся, что выражать следует ту переменную, при которой стоит более «удобный» коэффициент (в частности +- 1).

    Мы составили алгоритм решения системы методом подстановки.

    Формирование умений и навыков.

    Желательно, чтобы в течение урока учащиеся запомнили алгоритм решения систем уравнений методом подстановки и могли его применять, не обращаясь к записям в тетрадях и разобранным примерам.

    Задание на уроке: №12.5(аб), №12.2(а), №12.8(аб)

    Для решения каждой системы следует вызывать к доске по одному учащемуся. Необходимо требовать, чтобы они вслух комментировали все свои шаги.

    Контрольные вопросы:

    – Какие вы знаете способы решения систем уравнений?

    – Сформулируйте алгоритм решения систем уравнений способом подстановки

    – Из какого уравнения системы лучше выражать переменную?
    Задание на дом:

    №12.4(аб), №12.6(аб), 12.9(аб)

    написать администратору сайта