ТИПИС практическая работа 2. ТИПиС Практическая работа 2. Построение математических моделей с помощью

• Название: Построение математических моделей с помощью
• Анкор: ТИПИС практическая работа 2
• Дата: 28.02.2022
• Размер: 104.81 Kb.
• Имя файла: ТИПиС Практическая работа 2 .docx
• Тип: Отчет; #377138

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра АПУ


отчет

по практической работе №2

по дисциплине «Теория автоматического управления»

Тема: построение математических моделей с помощью simulink

Вариант № 3

Студент гр. 0326		Голинский А. А.
Преподаватель		Брикова О.И.

Санкт-Петербург

2021

СОДЕРЖАНИЕ

Задание 1 3

1.Текст задания 3

2. Вариант. 3

3. Выполнение задания 3

4. Ход работы 4

Вывод: 6

Задание 1

1. Текст задания

Построить компьютерную модель имитирующую падение и отскок в соответствии с заданными параметрами.

Деформацию мячика при падения принять равной 4,5 см.

2. Вариант.

Вариант №3

Данные шарика: h1=3(м), m=0.8(кг), h2=0.4*h1(м).

3. Выполнение задания

Используя программные средства simulink для реализации математической модели шарика, была получена следующая компьютерная модель, имитирующая падение и отскоки шарика. Модель приведена ниже на рисунке 1.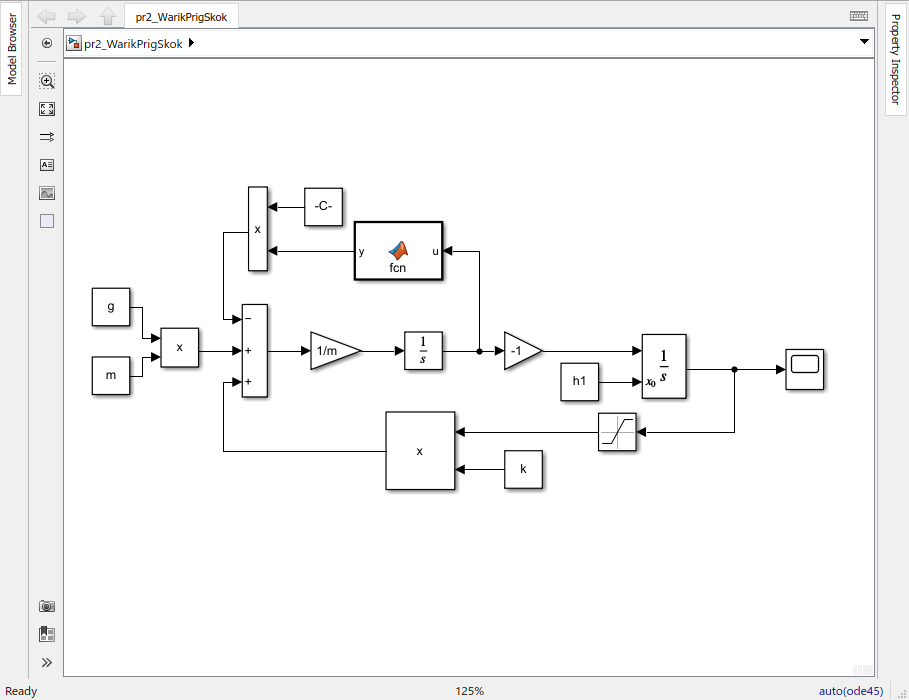



Рисунок 1 – Модель имитации отскоков шарика
С помощью вышеупомянутой модели, был получен следующий график последующих отскоков шарика, приведённый ниже на рисунке 2.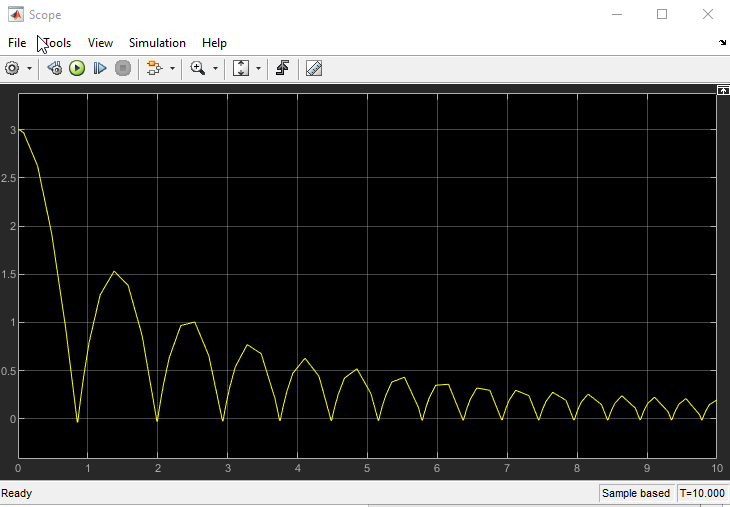

Рисунок 2 – График модели

4. Ход работы

Для построения модели шарика, было решено сначала описать его в физическом виде. Для этого был использован Второй закон Ньютона 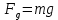(1)

(1)

Где Fg – сила тяжести, m - масса тела, а g – ускорение свободного падения, равное 9.8(м\с²).
Опишем время, за которое мячик упадёт на плоскость.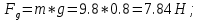


Найдём ускорение шарика.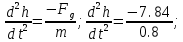

Найдём Скорость шарика.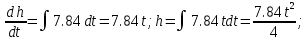


Теперь можно найти время, за которое шарик упадёт в первый раз.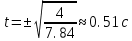
;

Далее необходимо смоделировать то, как шарик будет отскакивать от плоскости. Для этого используем Закон Гука (2), который выглядит следующим образом: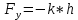

, (2)

Где 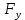– сила упругости тела, h – начальная высота падения, а k – коэффициент упругости.

Деформация шарика составляет 4.5 см, тогда чтобы определить коэффициент упругости, используем формулы, представленные ниже: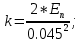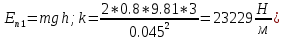

Мячик, отскакивая от поверхности, теряет высоту из-за силы сопротивления с воздухом: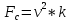

,

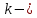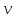где коэф. сопротивления; – скорость движения.

Для реализации этого нюанса, был использован блок MATLAB function, который позволил учесть сопротивление воздуха для последующих отскоков шарика. Функция внутри блока представлена на рисунке 3: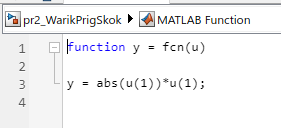



Рисунок 3 – Функция в MATLAB function.

Вывод:

В ходе практической работы были приобретены навыки использования MATLAB SIMULINK, а также разработана модель поведения шарика, брошенного на плоскость.