Курсовой проект автоматика. Курсововй автомтика. Построить годограф афчх разомкнутой системы

• Название: Построить годограф афчх разомкнутой системы
• Анкор: Курсовой проект автоматика
• Дата: 23.05.2022
• Размер: 278.87 Kb.
• Имя файла: Курсововй автомтика.docx
• Тип: Документы; #544930

Задание на курсовую работу
Для структурной схемы САУ, соответствующей выбранному варианту, выполнить следующие действия:

1. 
   Избавиться от всех перекрестных параллельных и обратных связей, привести структурную схему к стандартному виду. Определить передаточную функцию разомкнутой системы, записать ее в стандартной форме. Определить степень астатизма системы.
   
2. 
   Определить амплитудно-фазовую, вещественную и мнимую частотные характеристики разомкнутой системы.
   
3. 
   Построить годограф АФЧХ разомкнутой системы.
   
4. 
   Найти выражения для асимптотической ЛАЧХ и ЛФЧХ разомкнутой системы.
   
5. 
   Построить в масштабе ЛАЧХ и ЛФЧХ разомкнутой системы.
   
6. 
   Определить устойчивость замкнутой САУ с помощью критерия Найквиста и логарифмических частотных характеристик.
   
7. 
   Найти запасы устойчивости системы по фазе и по амплитуде.
   
8. 
   Найти передаточную функцию замкнутой системы и проверить выводы пункта 6 с помощью частотного критерия Михайлова.
   
9. 
   Определить величину поправочного коэффициента усиления, при котором статическая ошибка замкнутой системы будет не больше 0.1; перерегулирование в системе составит 12 %; время переходного процесса будет минимальным.
   
10. 
    Построить с переходную функцию замкнутой системы и оценить основные показатели качества регулирования (перерегулирование и время регулирования) в системе.
    
11. 
    Преобразовать полученную систему в цифровую форму и построить переходные процессы для различных значений шага квантования.
    

Исходные данные.

Вариант	Схема	k1	k2	k3	k4	k5	T1	T2	T3	T4	T5	T6	
12	(a)	2	0.8	4	15	2	0.75	0.15	0.95	0.1	0.6		0.4

Решение:
Упростим схему:


Где , .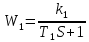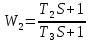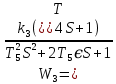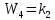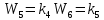

Перенесем сумматор.


Упростим систему.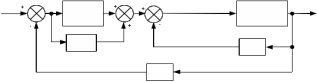

Где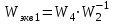
;

Где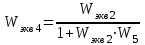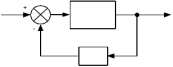
;

Где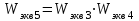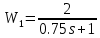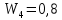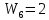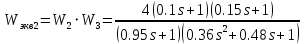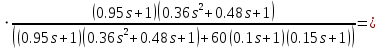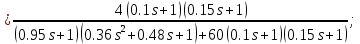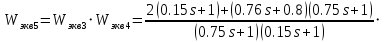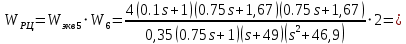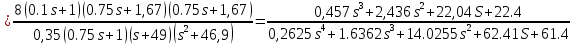


;

; ; ; ; .



;

;









Степень астатизма ν=0. Коэффициент передачи К=0.36. Постоянные времени: Т₁=0.1, Т₂=0.45, Т₃=0.45, Т₄=0,75, Т₅=0.020, Т₆=1, ξ=0.

2. Частотная передаточная функция системы (s→jω)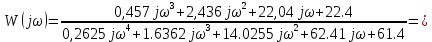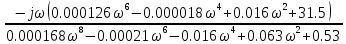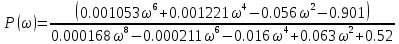











Особые точки АФЧХ приведены в таблице 1.

Таблица 1.

ω	0	2,85	∞
P(ω)	0.36	0	0
Q(ω)	0	-0.51	0

3. Годограф АФЧХ разомкнутой системы

Годограф (рисунок 1) при ω=0 начинается на положительной вещественной полуоси. При ω→ ∞ через четвертый и третий квадранты стремиться к нулю. Пересекает при ω=0 вещественную ось в точке (0.36;j0) и при ω=0.6 пересекает мнимую ось в точке (0;-j0.51).


4. Асимптотическая ЛАХ и ЛФХ

Вариант	Схема	k1	k2	k3	k4	k5	T1	T2	T3	T4	T5	T6	
12	(a)	2	0.8	4	15	2	0.75	0.15	0.95	0.1	0.6		0.4

Асимптотическая ЛАХ: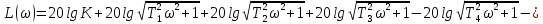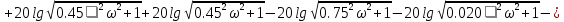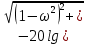


Т₁=0.1, Т₂=0.45, Т₃=0.45, Т₄=0,75, Т₅=0.020, Т₆=1, ξ=0.

Асимптотическая ЛФХ: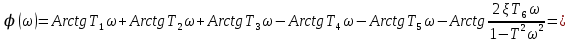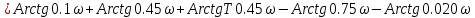




Построение в масштабе ЛАХ и ЛФХ системы



Устойчивость замкнутой САУ с помощью критерия Найквиста и логарифмических частотных характеристик

Степень астатизма системы ν=0 и характеристический полином разомкнутой системы имеет все корни в левой половине комплексной плоскости, то критерий Найквиста будет следующим: Для того чтобы замкнутая САУ была устойчивой необходимо и достаточно, чтобы годограф амплитудно-фазовой характеристики разомкнутой системы не охватывал точку с координатами (-1; j0).

На частотных характеристиках изображен годограф АФХ. Он не охватывает точку (-1; j0), следовательно, замкнутая система будет устойчивой.



Как видно из рисунка 4 годограф не пересекает отрицательную вещественную полуось, следовательно, запас устойчивости по амплитуде 100%.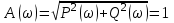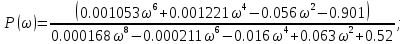







ω_ср=0,83 с^-1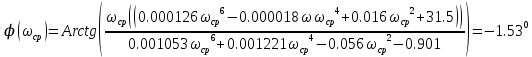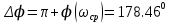





Таким образом запас по фазе составляет 39,23⁰.

Передаточная функция замкнутой системы может быть найдена по следующей формуле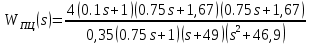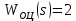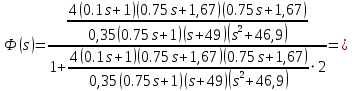







Характеристический полином системы: