Задания для самостоятельной работы. Поведение предприятия на отраслевом рынке задание 1 Постановка задачи
 Скачать 213.24 Kb. Скачать 213.24 Kb.
|
|
ЗАДАНИЕ 6 Определение оптимальных размеров предприятия Описание ситуации. При оптимальном размере предприятия обеспечивается выполнение плановых заданий по выпуску продукции и приросту производственных мощностей с минимальными приведенными затратами, максимальной прибылью и эффективностью. Приведенные затраты представляют собой сумму эксплуатационных затрат (себестоимости) и капиталовложений, приведенных к одинаковой годовой размерности с помощью нормативного коэффициента сравнительной эффективности. Приведенные затраты отражают полные совокупные затраты на содержание производства и выпуск продукции. При увеличении размера предприятия удельные капитальные затраты на единицу мощности и себестоимость единицы продукции уменьшаются (эффект масштаба), следовательно уменьшается и сумма приведенных затрат. Приведенные затраты на производство единицы продукции находятся в обратной зависимости к мощности предприятия, что приводит к появлению тенденции увеличения мощности, которая в свою очередь влияет на увеличение транспортных расходов. На основе статистических данных об изменении уровня затрат в зависимости от производственной мощности определить оптимальный размер предприятия. Исходные данные по вариантам: Вариант 1 Вариант 2
Вариант 3 Вариант 4
Вариант 5 Вариант 6
Методические указания по выполнению задания При оптимальном размере предприятия обеспечивается выполнение плановых заданий по выпуску продукции и приросту производственных мощностей с минимальными приведенными затратами, максимальной прибылью и эффективностью. Приведенные затраты представляют собой сумму эксплуатационных затрат (себестоимости) и капиталовложений, приведенных к одинаковой годовой размерности с помощью нормативного коэффициента сравнительной эффективности. Приведенные затраты отражают полные совокупные затраты на содержание производства и выпуск продукции и определяются по формуле: 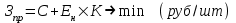 ; ; 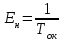 ; ; 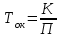 . . При увеличении размера специализированного предприятия удельные капитальные затраты на единицу мощности и себестоимость единицы продукции уменьшаются (эффект масштаба), следовательно уменьшается и сумма приведенных затрат. В общем виде зависимость между изменением мощности (M) и изменением приведенных затрат на производство единицы продукции определяется по формуле: 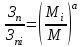 , , где Зп и Зпi - приведенные затраты на производство единицы продукции по известному и искомому вариантам, М и Мi - величины производственной мощности по известному и искомому вариантам, показатель степени а характеризует степень влияния мощности на приведенные затраты. 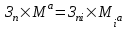 ; ; 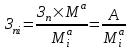 . .Приведенные затраты находятся в обратной зависимости к мощности предприятия, что приводит к появлению тенденции увеличения мощности, которая в свою очередь влияет на увеличение транспортных расходов. Взаимосвязь между мощностью и приведенными затратами на транспортировку выражается следующей формулой: 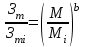 ; ; 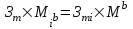 ; ; 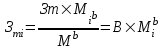 где показатель степени b характеризует влияние мощности на изменение транспортных расходов. Общая сумма производственных затрат составит: 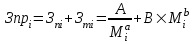 . . Чтобы определить оптимальную мощность предприятия, а следовательно и его размер, по критерию минимума приведенных затрат, необходимо продифференцировать функцию 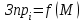 и приравнять производную к нулю: и приравнять производную к нулю: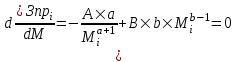 . . Откуда 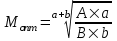 . . Для нахождения Мопт необходимо определить значения параметров А,а,B,b. Для чего необходимо путем логарифмирования привести к линейному виду формулы для расчета Зп и Зт , а затем воспользоваться методом наименьших квадратов. Необходимо определить оптимальное значение величины производственной мощности, характеризующей размер предприятия по критерию минимума приведенных затрат. Порядок выполнения кейс-задачи: представить формулу расчета оптимального значения величины производственной мощности, для чего продифференцировать функцию 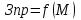 и приравнять производную к нулю; и приравнять производную к нулю;определить значения A,a,B,b методом наименьших квадратов, предварительно приведя к линейному виду формулы для расчета приведенных затрат на производство продукции и приведенных затрат на транспортировку продукции Метод наименьших квадратов В различных практических исследованиях приходится использовать формулы, полученные на основании опыта, наблюдения. Один из лучших способов получения таких формул – метод наименьших квадратов. Пусть, например, на основании эксперимента необходимо установить функциональную зависимость между температурой х и удлинением у рельса. По результатам измерений составляем таблицу:
Предположим, что эти точки координатной плоскости находятся приблизительно на одной прямой: 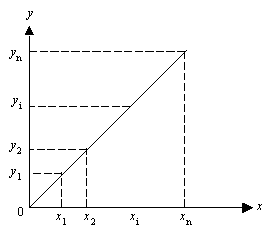 В данном случае естественно предположить, что между Y и X существует линейная зависимость, выражающаяся уравнением y=ax+b. Так как точки (xi,yi), i=1,n лишь приблизительно лежат на одной прямой, то равенства yi=axi+b будут выполняться приближенно, а величины погрешностей σi=yi-(axi+b) будут отличны от нуля. Составим следующую сумму: 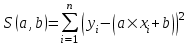 Подберем параметры a иb так, чтобы сумма квадратов погрешностей S(a,b) принимала наименьшие значения. Из необходимых условий экстремума следует: 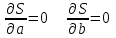 . .Тогда 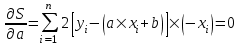 , ,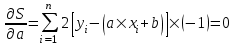 . .или 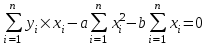 , ,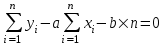 . .Решая эту систему, найдем значения a и b, подставив их в уравнение. |
