задачи с профессиональной направленностью. из опыта. Пояснительная записка Естественно математическая подготовка
 Скачать 309.68 Kb. Скачать 309.68 Kb.
|
|
Пояснительная записка Естественно - математическая подготовка является стержнем среднего профессионального образования по специальностям технического профиля и осуществлять ее необходимо в соответствии с требованиями федерального государственного образовательного стандарта общего образования и профессионального образования. В профилированной программе по математике для среднего профессионального образования основной задачей ставится укрепление межпредметных связей курса математики и дисциплин / курсов общепрофессионального и профессионального циклов. В связи с этим рекомендуются установление прочных связей в работе преподавателя математики и дисциплин, согласование общих целей, задач, требований: Иллюстрация математических понятий и предложений примерами, взятыми из содержания предметов профессиональной подготовки; Использование на занятиях математики учебно-наглядных пособий, применяемых на предметах профессиональной подготовки; Составление и решение задач по математике с профессионально- ориентированным содержанием, это позволяет вовлечь в активную познавательную деятельность даже самых «слабых» учащихся, позволяет показать практическую ценность математических знаний. Особенность профессионального образования и состоит в том, что интересы студентов в основном направлены на овладение профессии, и поэтому теоретический материал только тогда привлекает внимание будущих рабочих и специалистов среднего звена, когда они видят его практическую значимость для своей последующей производственной деятельности. Cреди учебных пособий, которые применяются для обучения математике, в основном преобладают учебники, сборники и задачники, ориентированные на учащихся школ, а для системы СПО таких пособий немного, и то в них недостаточно заданий по тем разделам математики, которые заложены в ЕГЭ. Тем более, что многие наши выпускники планируют продолжить обучение по выбранной специальности в ВУЗах. Таким образом, в данном сборнике представлены материалы, которые можно использовать при организации и проведении практических, аудиторных и внеаудиторных самостоятельных работ. На занятиях различного типа: изучения нового материала, формирования и совершенствования ЗУН, обобщения и систематизации знаний. Предлагаемый сборник включает задачи по следующим темам: Задачи на выполнение арифметических действий (целые, рациональные и дробные числа) необходимых в практической и профессиональной деятельности. Задачи с процентами. Понятие процента. Нахождение процента от числа (величины), нахождения числа по его проценту, нахождение процента одного числа от другого. Пропорция. Прямая и обратная пропорциональность. Задачи с графическим представлением данных. Анализ данных. Задачи, заданные табличным способом на нахождение наибольшего и наименьшего значения. Решение задач о транспортировке груза, о выборе тарифа, об аренде автомобиля, о расходах на ремонт автотранспорта, о покупке запчастей, о трех дорогах, о покупке стройматериалов. Текстовые задачи. Решение задач на движение, производительность. Комбинированные задачи. Текстовые задачи на моделирование процессов. Решение задач на анализ явления, описываемого формулой функциональной зависимости (линейной, степенной, показательной, логарифмической, тригонометрической). Функциональные зависимости в профессионально- ориентированных задачах. Применение производной в практической и профессиональной деятельности. Геометрические задачи. Решение практических, профессионально - ориентированных задач по темам: «Многогранники. Формулы нахождения площадей поверхностей, объемов тел, площадей, 1.Целые, рациональные и дробные числа1 литр бензина АИ-92 стоит 33 рубля 62 коп. На заправочной станции водитель залил в бак 25 литров. Сколько рублей сдачи он должен получить с 1000 рублей? В отделе «Автокосметика» ТЦ «За рулем» объявлена акция: при покупке 4 флаконов автошампуня пятый в подарок. Сколько флаконов автошампуня может купить автолюбитель на 1450 рублей, если 1 флакон стоит 132 рубля? Для автомобиля полагается купить количество шин кратных 4. Автошина стоит 3200 рублей. У ООО «Шиномонтаж» 460 тыс. рублей. Какое наибольшее количество автомобилей одной модели будут обеспечены шинами? На спидометре американского автомобиля скорость указывается в милях в час. Американская миля равна 1609 м. Какова скорость автомобиля в километрах в час, если спидометр показывает 75 миль в час? Ответ округлите до целого числа. Спидометр автомобиля показывает скорость в милях в час. Какую скорость (в милях в час) показывает спидометр, если автомобиль движется со скоростью 40 км/ч? (Считайте, что 1 миля = 1,6 км.) Таксист за месяц проехал 6000 км. Стоимость 1 л бензина 34 рубля. Средний расход бензина на 100 км составляет 9 л. Сколько рублей потратил таксист на бензин за этот месяц? Задачи с процентамиЦена на ремень ГРМ (ремень газораспределительного механизма) была повышена на 23% и составила 1845 рублей. Сколько рублей стоил ремень ГРМ до повышения цены? В двух канистрах находится 90 л бензина. Если из первой канистры перелить во вторую 10% бензина, находящегося в первой канистре, то в обеих канистрах станет поровну. Сколько литров бензина было в каждой канистре? Баллон антикоррозийного средства «WD-40» стоит 40 рублей. Какое наибольшее число таких баллонов можно будет купить на 500 рублей после повышения цены на 20%? 1 литр масла ДВС стоил 500 рублей. После снижения цены стал стоить 380 рублей. На сколько процентов была снижена цена? Мойка автобуса стоит 820 рублей. Стоимость мойки легкового автомобиля составляет 60% от стоимости мойки автобуса. Организации требуется помыть 2 автобуса и 6 легковых автомобилей. Сколько рублей организации потребуется для оплаты услуги? В магазине автозапчастей находится 4500 наименований товара, причем 42% из них автомобильные аксессуары. Известно, что из аксессуаров 80% не является эмблемами. Сколько эмблем в магазине? 3. Задачи с графическим представление данных. Анализ данных На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска автомобиля, на вертикальной оси – температура двигателя в 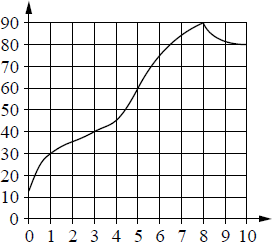 градусах Цельсия. градусах Цельсия.Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.
2.На диаграмме показано количество посетителей сайта для подбора автозапчастей и аксессуаров для автомобиля «Auto.ru» в течение каждого часа 8 декабря 2014 года. По горизонтали указывается часы, по вертикали — количество посетителей сайта за данный час. Определите по диаграмме, каким было наименьшее количество посетителей в час с 11:00 до 17:00 в этот день на сайте. 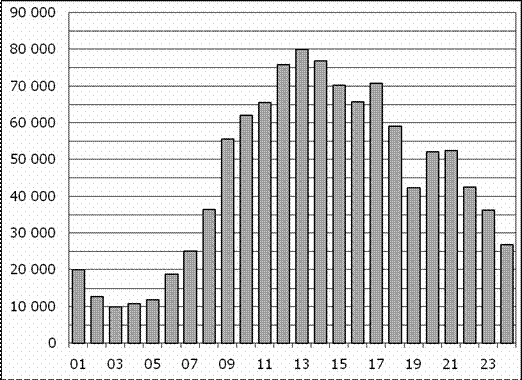 3.На графике показано изменение скорости движения автомобиля в зависимости от времени. На оси абсцисс отмечается время движения в часах, на оси ординат – скорость в километрах в час. Сколько часов автомобиль двигался со скоростью не менее 60 км/ч? 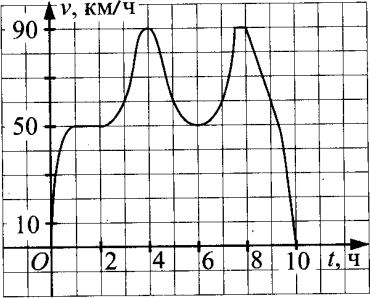 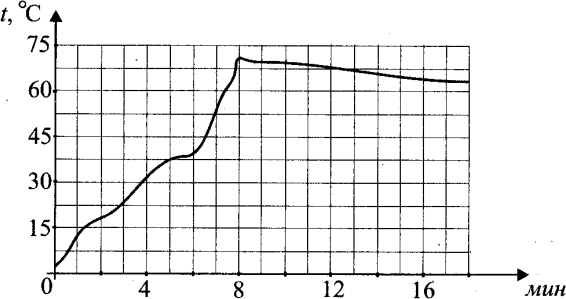 4.На графике показан процесс разогрева двигателя легкового автомобиля при температуре окружающего воздуха 30С. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат – температура двигателя в градусах Цельсия. Когда температура достигает определенного значения, включается вентилятор, охлаждающий двигатель, и температура начинает понижаться. Определите по графику, сколько минут прошло с момента запуска двигателя до включения вентилятора? 4.На графике показан процесс разогрева двигателя легкового автомобиля при температуре окружающего воздуха 30С. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат – температура двигателя в градусах Цельсия. Когда температура достигает определенного значения, включается вентилятор, охлаждающий двигатель, и температура начинает понижаться. Определите по графику, сколько минут прошло с момента запуска двигателя до включения вентилятора?5. На графике изображена зависимость крутящего момента двигателя от числа оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат – крутящий момент в Н·м. Скорость автомобиля (в км/ч) приближенно выражается формулой v=0,03n, где n- число оборотов двигателя в минуту. С какой наименьшей скоростью должен двигаться автомобиль, чтобы крутящий момент был не меньше 75 Н·м? Ответ дайте в километрах в час. 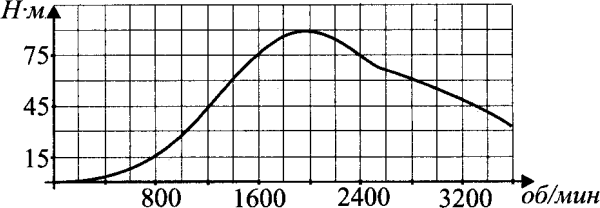 6.На рисунке жирными точками показано количество запросов со словами «ремонт автомобиля», сделанных на поисковом сайте Yandex.ru во все месяцы с марта 2008 по октябрь 2009 года. По горизонтали указываются месяцы, по вертикали — количество запросов за данный месяц. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольшее месячное количество запросов со словами «ремонт автомобиля» в период с сентября 2008 по май 2009 года. 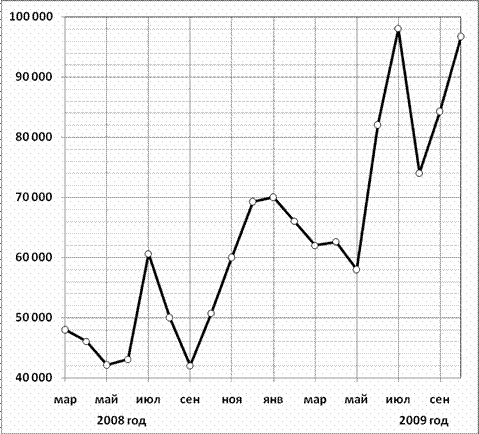 7.На графике показано изменение температуры воздуха в гараже на протяжении трех суток, начиная с 0 часов вторника. На оси абсцисс отмечается время суток в часах, на оси ординат — значение температуры в градусах. Определите по графику наименьшую температуру воздуха в ночь со среды на четверг. 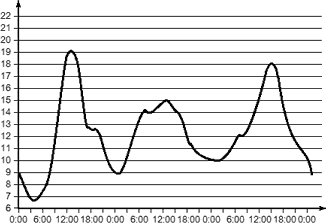 4.Задачи, заданные табличным способом на нахождение наибольшего и наименьшего значенияСемья из трех человек планирует поехать из Улан-Удэ в Иркутск. Можно ехать поездом, а можно — на своей машине. Билет на поезд на одного человека стоит 930 рублей. Автомобиль расходует 10 литров бензина на 100 километров пути, расстояние по шоссе равно 500 км, а цена бензина АИ-92 равна 34 рубля за литр. Сколько рублей придется заплатить за наиболее дешевую поездку на троих? Клиент хочет арендовать автомобиль на сутки для поездки протяженностью 600 км. В таблице приведены характеристики трех автомобилей и стоимость их аренды. Помимо аренды клиент обязан оплатить топливо для автомобиля на всю поездку. Какую сумму в рублях заплатит клиент за аренду и топливо, если выберет самый дешевый вариант?
Цена дизельного топлива — 16 рублей за литр, бензина — 18 рублей за литр, газа — 15 рублей за литр. Для транспортировки 45 тонн груза на 1300 км можно использовать одного из трех перевозчиков. Стоимость перевозки и грузоподъемность автомобилей для каждого перевозчика указана в таблице. Сколько рублей придется заплатить за самую дешевую перевозку за один рейс? 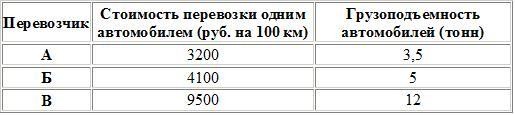 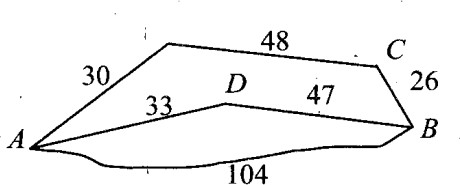 Из пункта А в пункт В ведут три дороги (см. рис., расстояния указаны в километрах). Через пункт С едет автобус со средней скоростью 65 км/ч, через пункт D едет грузовик со средней скоростью 60 км/ч, и по третьей дороге без промежуточных пунктов едет легковой автомобиль со средней скоростью 80 км/ч. Все три машины выехали из пункта А одновременно. Найдите время в пути (в часах) автомашины, пришедшей позже всех. Из пункта А в пункт В ведут три дороги (см. рис., расстояния указаны в километрах). Через пункт С едет автобус со средней скоростью 65 км/ч, через пункт D едет грузовик со средней скоростью 60 км/ч, и по третьей дороге без промежуточных пунктов едет легковой автомобиль со средней скоростью 80 км/ч. Все три машины выехали из пункта А одновременно. Найдите время в пути (в часах) автомашины, пришедшей позже всех.Из пункта А в пункт В ведут три дороги (см. рис.). Через пункт B едет трактор со средней скоростью 44 км/ч, через пункт С едет легковой автомобиль со средней скоростью 68 км/ч. Третья дорога без промежуточных пунктов, и по ней движется автобус со средней скоростью 45 км/ч. Все три автомобиля одновременно выехали из пункта А. Какой автомобиль добрался до пункта D раньше других? В ответе укажите, сколько часов он находился в дороге. 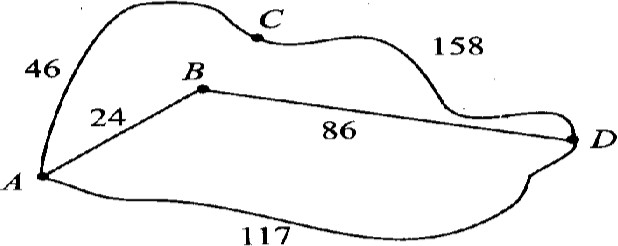 6. Первые два часа автомобиль ехал со скоростью 95 км/ч, следующие два часа — со скоростью 45 км/ч, а затем один час — со скоростью 40 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. 7. Автомобиль ехал 1,5 часа со скоростью 40 км/ч, 2,5 часа – со скоростью 60 км/ч, оставшуюся часть пути – со скоростью 75 км/ч. Определите среднюю скорость автомобиля, если всего он потратил 5 часов. Ответ укажите в км/ч. 8. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 12 км/ч, а вторую половину пути — со скоростью 72 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 45 км/ч. 5. Комбинированные задачи1.При температуре 0°С выхлопная труба легкового автомобиля имеет длину l0 = 3,25 метров. При возрастании температуры происходит тепловое расширение трубы, и его длина, выраженная в метрах, меняется по закону: l(t°) = l0 · (1 + a · t°), где a = 1,2 · 10−5 (°C)−1 — коэффициент теплового расширения, t° — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия. 2.Коэффициент полезного действия (КПД) двигателя (ДВС) определяется по формуле: температуры нагревателя T1 КПД этого двигателя будет не меньше 70%, если температура холодильника T2 = 150? 3.Коэффициент полезного действия (КПД) некоторого двигателя определяется по формуле: минимальной температуре нагревателя T1 КПД этого двигателя будет не меньше 20%, если температура холодильника T2 = 310 К? Ответ выразите в градусах Кельвина. 4.В боковой стенке высокого цилиндрического бака у самого дна закреплен кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону: 6. Применение логарифмической и показательной функции в жизни и профессиональной деятельности 1.Необходимо вычислить стоимость оборудования станции технического обслуживания (СТО) через 5 лет, если его первоначальная стоимость ежегодный процент амортизации =5,7% 2.Стоимость оборудования автомастерской равна 500 тыс. р. Известно, что через 10 лет стоимость этого оборудования вследствие амортизации будет равна 200 тыс. р. Найдите процент ежегодной амортизации оборудования. 3. Количество автомобилей в городе возрастает ежегодно на 3%. Через сколько лет количество автомобилей в этом городе увеличиться в 1,5 раза? 4.Какова была численность населения города 10 лет тому назад, если в настоящее время в городе проживает 300 тыс. человек, а ежегодный прирост составляет 3,5% 7.Применение производной в практической и профессиональной деятельности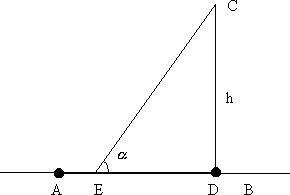 1.Каким должен быть угол примыкания 1.Каким должен быть угол примыкания Рис. 1 2. Закон прямолинейного движения задан уравнением s=-t3+9t2-24t-8. Найти максимальную скорость движения тела (s-вметрах, t- всекундах). 3.Тело движется по закону s(t)=18t2+10t-2t3(s- в метрах,t-в секундах). Найдите максимальную скорость движения тела. 4.Материальная точка движется по закону s(t)=12t2-2 t3.В какой момент времени t- 3 м/с, скорость точки будет наибольшей. 8.Геометрические задачи1.Бак, имеющий форму прямоугольного параллелепипеда, доверху заполнен бензином. Длина бака 3 м, ширина 1,5 м, высота 1,2 м (размеры внутренние). Плотность бензина 710 кг/м3. На сколько рабочих дней хватит этого бензина для заправки автомобиля ГАЗ-53, если средний расход бензина автомобилем за рабочий день 95 кг? 2. Кузов тракторного прицепа имеет усеченной пирамиды и размеры: вверху 3,5 м х 2,6 м, понизу 2,9 м х 1,1 м. Найдите вместимость, если высота прицепа 1,2 м. Надо изготовить цилиндрическую цистерну для масла, закрытую сверху. Диаметр ее основания 450 см, высота 220 см. Сколько листов листовой стали размером 100 см х 600 см пойдет на ее изготовление? На швы и обрезки добавить 12% площади. Найти вес железной цилиндрической трубки, внутренний диаметр которой равен 17 см, а внешний диаметр равен 18 см, а длина равна 74 см. Плотность железа 7,9 г/см3. На цилиндрический барабан подъемной машины, диаметр которого 750 мм, а ширина 350 мм, наматывается стальной трос толщиной 20 мм. Сколько метров каната помещается в один ряд на поверхности барабана? Диаметр цилиндра паровой машины равен 330 мм, ход поршня 406 мм. Найти объем рабочей части цилиндра с точностью до 0,1 дм3. 100 кубических сантиметров масла, вылитые на поверхность воды образовали пленку в форме круга диаметром 18 м. Определить толщину пленки. В цилиндрическую цистерну емкостью 12 т налито дизельное топливо. Сколько дизельного топлива содержится в цистерне, если ее высота равна 6 м, а уровень горючего 2 м? Сколько бочек высотой 1,5 м и диаметром 0,8 м нужно, чтобы разлить в них содержимое цистерны длиной 4,5 м и диаметром 1,6 м? ЛитератураБашмаков М.И. Математика: алгебра и начала математического анализа, геометрия. Базовый уровень: учебник для 10,11 класса.- М.: Бином. Лаборатория знаний, 2019 Л.С.Атанасян и др. Геометрия, 10-11классы. – М.: Просвещение, 2021. Сборник задач по математике: учеб. Пособие для ссузов/Н.В.Богомолов. – 5-е изд., стереотип. – М.: Дрофа, 2019. – 204, [4] с.: ил. Интернет-ресурсы: http://www.tgl.net.ru/wiki/index.php/Прикладная_и_практическая_направленность_о бучения_математике http://www.berdov.com/ege/ http://www.ege.edu.ru/ - демоверсии КИМов ЕГЭ по математике одобренных ФИПИ http://mathege.ru/ http://www.matematika-ege.ru/ege2010/ http://www.problems.ru http://mat.1september.ru http://www.uchportal.ru/ http://www.zavuch.info/ http://nsportal.ru/ http://www.exponenta.ru/educat/links/l_educ.asp#0 – Полезные ссылки на сайты математической и образовательной направленности: Учебные материалы, тесты http://www.fxyz.ru/ - Интерактивный справочник формул и сведения по алгебре, тригонометрии, геометрии, физике. http://maths.yfa1.ru - Справочник содержит материал по математике (арифметика, алгебра, геометрия, тригонометрия). allmatematika.ru - Основные формулы по алгебре и геометрии: тождественные преобразования, прогрессии, производная, стереометрия и проч. |
