Курсовая по Теории автоматического управления. Курсовая. Пояснительная записка к курсовой работе по дисциплине Основы теории автоматического управления

• Название: Пояснительная записка к курсовой работе по дисциплине Основы теории автоматического управления
• Анкор: Курсовая по Теории автоматического управления
• Дата: 16.11.2022
• Размер: 0.89 Mb.
• Имя файла: Курсовая.docx
• Тип: Пояснительная записка; #792642

 

 

                                                                                                      Оценка работы:

                                                                                                    

  ________________

 

 

 

А1222 06 393512 000 000 ПЗ

Разработка и моделирование систем автоматического управления

Пояснительная записка к курсовой работе по дисциплине

«Основы теории автоматического управления»

 

 

 

 

Руководитель:
Студент:
Группа:

 

                                                         

Задание

Построить модель объекта управления двумя способами: многоконтурную систему подчинённого регулирования. Система должна быть разработана в двух вариантах: непрерывном и дискретном.

Для разработки многоконтурной системы объект должен быть представлен в виде схемы из звеньев с известными передаточными функциями. Все звенья модели должны быть реальными. В явном виде на схеме должны присутствовать переменные u, x, y, z.

К системам предъявляются следующие требования:

1. 
   Время переходного процесса t_пп = 0.2+0.25*N = 0.2+0.25*6= 1.7 с;
   
2. 
   Погрешность времени переходного процесса во всех случаях не должна превышать 2%;
   
3. 
   Системы должны иметь первый порядок астатизма;
   
4. 
   В управляющей части многоконтурного управления использовать только звенья типа пропорциональный усилитель, интегратор и реальный дифференциатор;
   
5. 
   Вид переходного процесса должен соответствовать распределению полюсов по Баттерворту.
   

Выполнение заданных требований должно быть подтверждено моделированием в MATLAB-Simulink.

Оглавление

Задание 2

Исходные данные 4

1.Подготовка моделей объекта управления 5

1.1 Модель ОУ для многоконтурной САР 5

2.Разработка и моделирование непрерывной многоконтурной САР 6

2.1 Разработка непрерывной многоконтурной САР 6

2.2 Моделирование непрерывной многоконтурной САР 10

3.Разработка и моделирование дискретной многоконтурной САР 13

3.1. Разработка дискретной многоконтурной САР 13

3.2 Моделирование дискретной многоконтурной САР 16

Исходные данные

Варианту № 6 соответствует следующая система уравнений, описывающих объект управления (ОУ):

, где

x, y, v – внутренние переменные ОУ,

u – задающее воздействие,

z – главная регулируемая величина.

Переменные x, y, z, а также их производные доступны для прямого измерения, а переменная v не доступна для измерения, при этом v = Nu, где N – номер варианта. Тогда v = 6u.

Все переменные являются функциями времени.

1. Подготовка моделей объекта управления

1.1 Модель ОУ для многоконтурной САР

Согласно заданию, ОУ описывается следующими уравнениями:



Преобразование Лапласа:



Выразим переменные:



По данным уравнения составим модель объекта управления:



Рисунок 1. Исходная модель объекта управления

2. Разработка и моделирование непрерывной многоконтурной САР

2.1 Разработка непрерывной многоконтурной САР

В общем виде система должна принять следующий вид (рис. 5):



Рисунок 2. Общий вид многоконтурной системы автоматического регулирования







Так как в системе объекта управления присутствует обратная связь, то, согласно рисунок 2, ее необходимо компенсировать. Она примет следующий вид (рисунок 3):



Рисунок 3. Модель объекта управления с компенсацией обратной связи

Исходя из заданных свойств системы, необходимо принять желаемую передаточную функцию системы. В нашем случае это будет апериодическое звено первого порядка. Для него желаемая передаточная функция примет следующий вид:



Для обеспечения выполнения требования по порядку астатизма K = 1.

Передаточная функция такой системы в разомкнутом виде будет следующая:



Путем перехода от желаемой функции замкнутой системы к желаемой функции разомкнутой получим переходную функцию регулятора: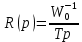



Найдем регуляторы первого, второго и третьего контура исходя из полученной функции: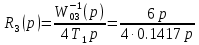







Где



Данные звенья получились идеальными, поэтому необходимо привести их к реальным: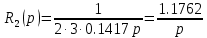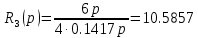









Рисунок 4. Регулятор третьего контура

Звено 10.5857 регулятора R₃(p) – является пропорциональным звеном.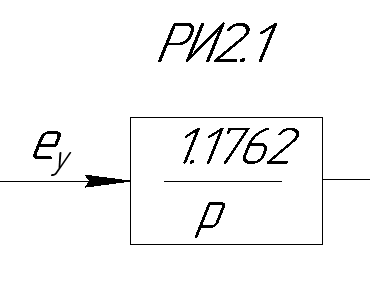



Рисунок 5. Регулятор второго контура

Звено регулятора R₂(p) – является интегрирующим звеном.



Рисунок 6. Регуляторы первого контура

Так как звено R₂(p) было нереализуемым, было принято решение ввести переменную T_дp, при этом значение T_д должно быть в пределах 0.002…0.1. По результатам построений было принято решение взять 0.002.

Звено регулятора R₃(p) – является интегральным звеном.

В конечном виде схему можно представить следующим образом (рисунок 7):



Рисунок 7. Многоконтурная система автоматического регулирования

2.2 Моделирование непрерывной многоконтурной САР

Собранная модель представлена на рис. 8.



Рисунок 8. Система многоконтурного управления в matlab

График выходной величины z при единичном ступенчатом сигнале в качестве задания показан на рис. 9.

При дальнейшем изучении процесса видно, что требования соблюдены: порядок астатизма равен единицы (установившаяся ошибка равна нулю,
рис. 10), распределение полюсов соответствует Баттерворту (перерегулирование не больше 8%, рис. 11), погрешность времени переходного процесса не превышает 2% (при t_пп = 1.7 сдопустимый диапазон составит 1.666...1.734 с,рис. 12).


t, c

z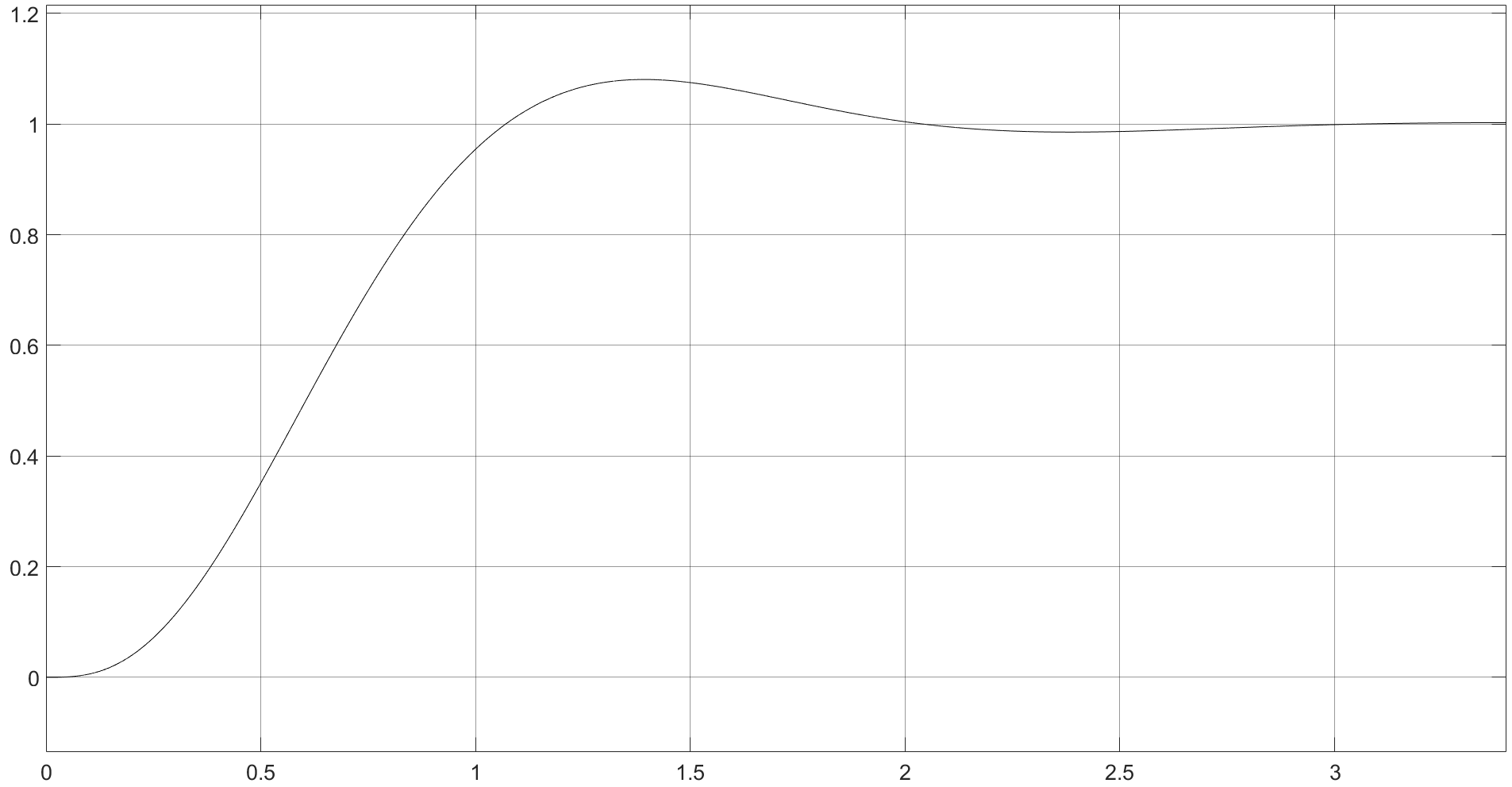


Рисунок 9. Реакция многоконтурной системы управления на единичный сигнал управления


t, c

z


Рисунок 10. Статическая ошибка многоконтурной системы управления


t, c

z


Рисунок 11. Перерегулирование многоконтурной системы управления


z

t, c


Рисунок 12. Время переходного процесса многоконтурной системы управления

3. Разработка и моделирование дискретной многоконтурной САР

3.1. Разработка дискретной многоконтурной САР

По правилу трапеций принимаем , где Т – период дискретности

Для звена R3.1: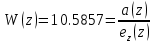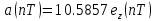









Для звена R2.1: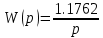











Для звена R1.1: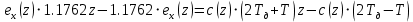









Для звена R1.2:











Алгоритм работы представлен на рис.13.



Рисунок 13. Алгоритм работы контроллера дискретной многоконтурной системы автоматического регулирования

3.2 Моделирование дискретной многоконтурной САР

Созданная модель рис. 14:



Рисунок 14. Система дискретной многоконтурной системы автоматического управления в matlab

Модуль подсистемы рис. 15: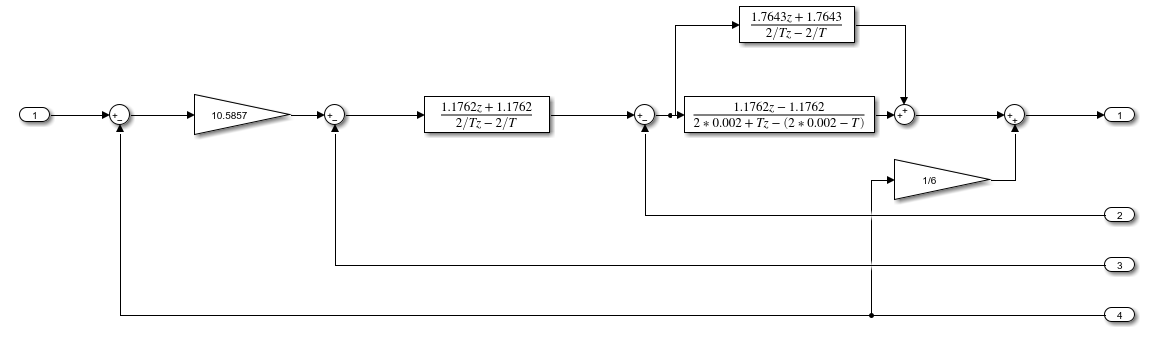



Рисунок 15. Подсистема дискретной многоконтурной системы автоматического управления в matlab

График выходной величины z при единичном ступенчатом сигнале показан на рис. 16. Как можно видеть на нем отличия дискретной САР от непрерывной мало при малом периоде дискретности Т.


z – непрерывная система

z* - дискретная система

t, c

z

z*


Рисунок 16. Сравнение реакций непрерывной и дискретной систем много контурного управления

При изучении графика видно, что все требования соблюдены: порядок астатизма равен единицы (установившаяся ошибка равна нулю, рис. 17), распределение полюсов соответствует Баттерворту (перерегулирование не больше 8%, рис. 18), погрешность времени переходного процесса не превышает 2% (при t_пп = 1.7 сдопустимый диапазон составит 1.666...1.734 с,рис. 19).


t, c

z = z*

z

z*


Рисунок 17. Статическая ошибка дискретной многоконтурной системы автоматического управления


z – непрерывная система

t, c

z* - дискретная система

z

z*


Рисунок 18. Сравнение перерегулирования непрерывной и дискретной многоконтурной системы автоматического управления


z – непрерывная система

z* - дискретная система

t, c

z

z*


Рисунок 19. Сравнение времени переходного процесса непрерывной и дискретной системы автоматического управления

Для подбора максимального периода дискретности, при котором САР удовлетворяет требованию 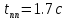, был проведен ряд опытов, результаты которых представлены в табл. 1. Период дискретности подбирался с точностью в 0,001 с. В результате было выбрано значение T = 0,01 с.

Таблица 1. Подбор периода дискретности T

T	0,1	0.08	0.06	0.04	0.03	0.02	0.01
tпп	1.505	1.5437	1.5805	1.6291	1.6331	1.65	1.666

Модель дискретной системы с реализацией управляющей части во временной области представлена на рисунках 20, 21, 22.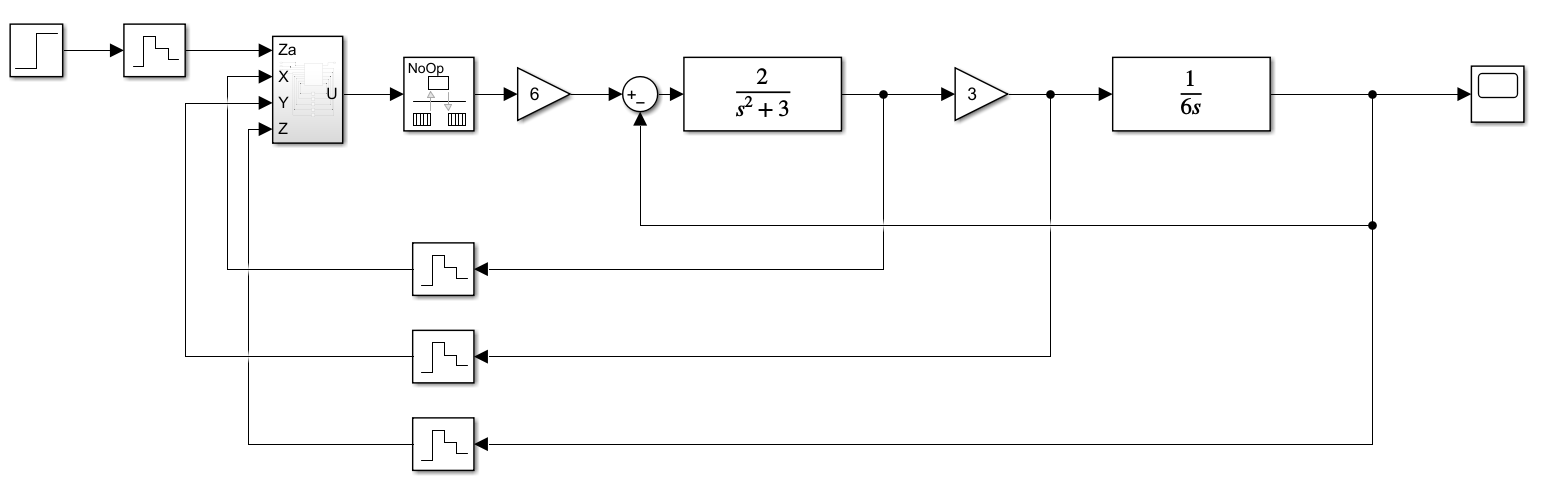



Рисунок 20. Модель дискретной системы с реализацией управляющей части во временной области

Модуль подсистемы рис. 21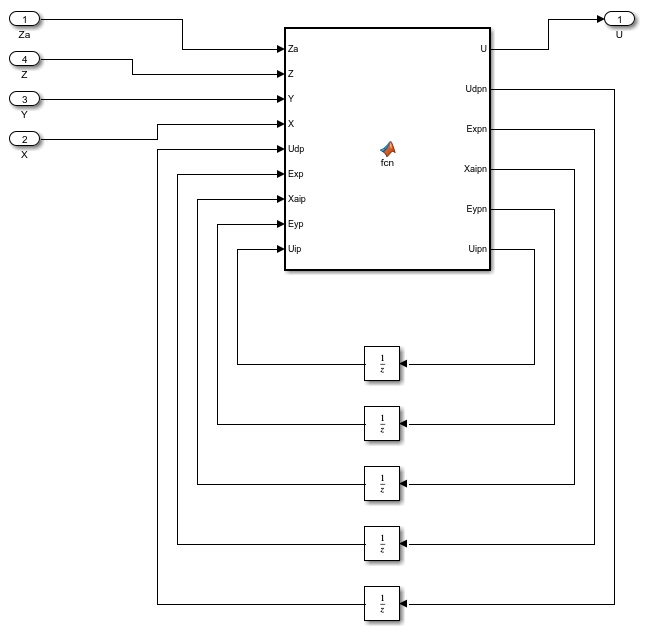



Рисунок 21. Модуль подсистемы модели дискретной системы с реализацией управляющей части во временной области

Формулы, заложенные в функцию рис. 22



Рисунок 22. Формулы, заложенные в подсистему модели дискретной системы

Результат моделирования системы и сравнение графиков рис. 23


t, c

z = z*

z

z*


Рисунок 23. Сравнение реакций систем дискретных систем управления

Результат работы двух систем представлен на рисунке 24 (z – непрерывная многоконтурная САР, z* - дискретная многоконтурная САР)


z*

z

Рисунок 24. Результат реакций непрерывной и дискретной много контурной системы управления

z*

z

t, c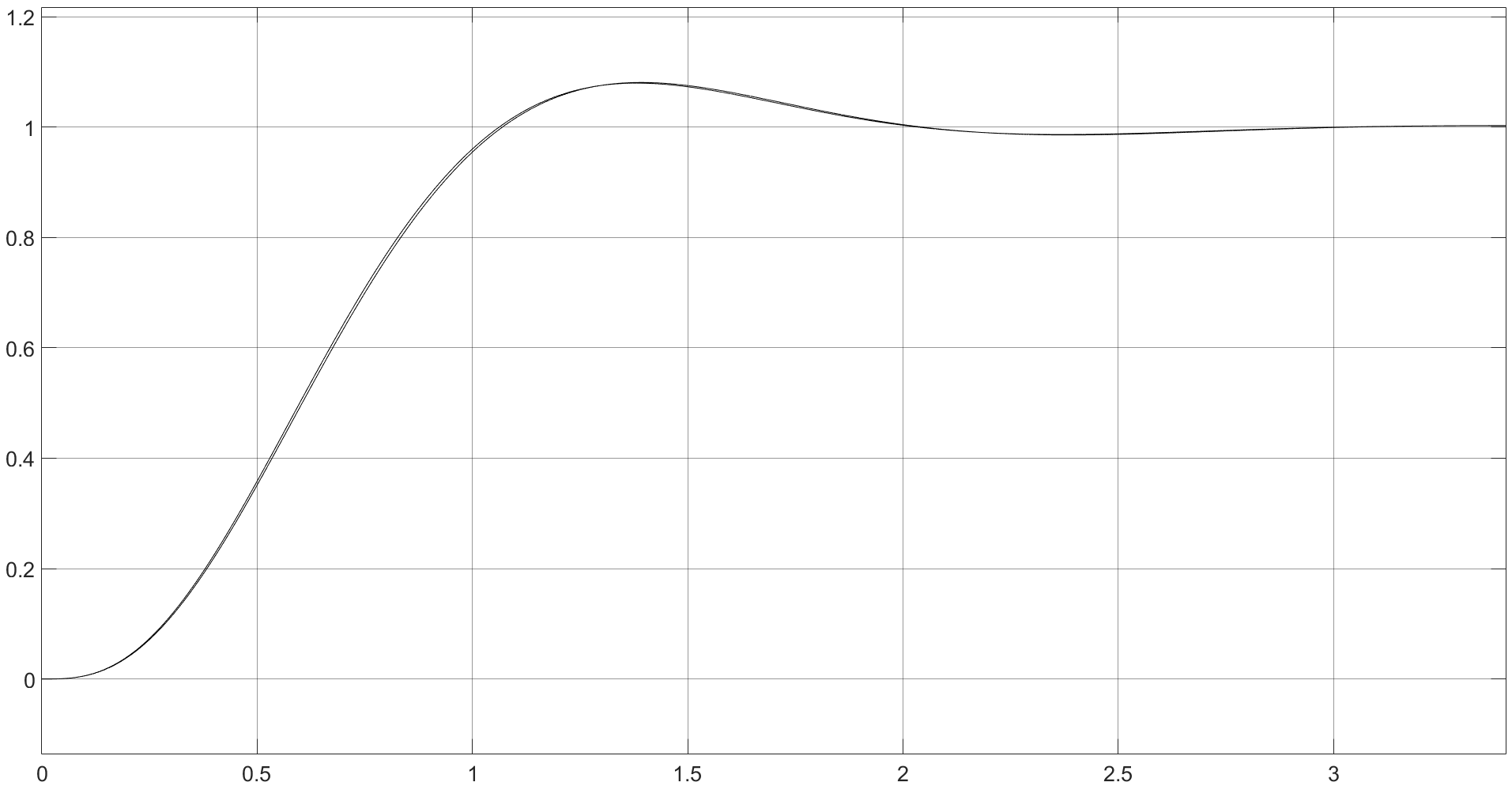