Сигналы электросвязи. Пояснительная записка к курсовой работе по дисциплине Радиотехнические цепи и сигналы Вариант 18 студент гр

Название	Пояснительная записка к курсовой работе по дисциплине Радиотехнические цепи и сигналы Вариант 18 студент гр
Анкор	Сигналы электросвязи
Дата	22.06.2022
Размер	0.8 Mb.
Формат файла
Имя файла	Сигналы электросвязи.docx
Тип	Пояснительная записка #610316

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ

УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра телекоммуникаций и основ радиотехники (ТОР)

ДИСКРЕТНАЯ ОБРАБОТКА СИГНАЛОВ
И ЦИФРОВАЯ ФИЛЬТРАЦИЯ
Пояснительная записка к курсовой работе

по дисциплине «Радиотехнические цепи и сигналы»
Вариант 18

Выполнил: студент гр.

«___»______________ 2020 г.

Проверил:

«___»______________ 2020 г.
Томск 2020

Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра телекоммуникаций и основ радиотехники (ТОР)
ЗАДАНИЕ

на курсовую работу по дисциплине «Радиотехнические цепи и сигналы»
«ДИСКРЕТНАЯ ОБРАБОТКА СИГНАЛОВ
И ЦИФРОВАЯ ФИЛЬТРАЦИЯ»
Студентугруппафакультет

Исходные данные:

1.1 Номер варианта – 18
1.2 Модель аналогового сигнала

Шифр N₁N₂	График сигнала
11

1.3 Временная структура аналогового сигнала

Шифр N₃N₄	t₁	t₂	t₃	T_OC
07	70 мкс	1,5t₁	2,5t₁	3,5t₁

1.4 Модель линейной электрической цепи (аналогового фильтра-прототипа)

Шифр N₅N₆	Модель линейной электрической цепи
07

1.5 Задание варианта цифрового фильтра

Шифр N₇N₈	Тип аппроксимации АЧХ (наименование окна)	Метод синтеза цифрового фильтра	Тип импульсных характеристик	Тип ЦФ
05	Бартлетта	Метод частотной выборки	КИХ (ТЦФ)	ФНЧ

1.6 Параметры затухания А_П и А_З АЧХ цифровых ФНЧ и нормированные граничные частоты полос пропускания

и заграждения

Шифр N₉N₁₀	Неравномерность (А_П) АЧХ в пределах полосы пропускания, дБ	Затухание (А_З) АЧХ в полосе заграждения, дБ	Нормированные граничные частоты полос пропускания и заграждения

18	1,0	15	0,1	0,15

Задание

Задание на первую часть курсовой работы

Дискретизировать заданный шифром N₁N₂ сигнал и восстановить аналоговый сигнал, используя ряд Котельникова. При определении наивысшей частоты спектра сигнала использовать пороговый критерий
(для f>f_max амплитуды спектральных составляющих, не превышают уровня 0,1 от максимальной).
Рассчитать спектр дискретной последовательности, определенной в пункте 2.1.1. Построить график.
Найти Z-преобразование найденной в п. 2.1.1 дискретной последовательности.
Определить дискретное преобразование Фурье (ДПФ)той же дискретной последовательности. Построить график. Восстановить аналоговый сигнал, используя тригонометрический ряд Фурье.
По результатам пункта 2.1.4 найти исходную дискретную последовательность. Построить график.
Произвести сравнение результатов вычислений:

1) сравнит форму спектра дискретизированной последовательности со спектром исходного аналогового сигнала;

2) установить связь между:

а) результатом Z-преобразования и спектральной плотностью дискретной последовательности;

б) между спектром исходного периодического аналогового сигнала и дискретными отсчетами его спектральной плотности.

Задание на вторую часть курсовой работы Вариант I

Для заданной шифром N₅N₆ аналоговой линейной электрической цепи найти операторное выражение передаточной функции К(р) и импульсную характеристику g(t).
Осуществить синтез цифровой цепи методом билинейного
Z-преобразования по найденной в п. 2.2.1 К(р). Построить схему алгоритма цифрового фильтра (ЦФ).
Произвести синтез ЦФ с помощью метода инвариантности импульсной характеристики (ИИХ) по найденной в пункте 2.2.1 g(t). Построить схему алгоритма ЦФ.
Найти отклик ЦФ в виде выходной дискретной последовательности на входную дискретную последовательность, полученную в пункте 2.1.1, на основе выполнения пунктов 2.2.2 или 2.2.3 с помощью обратного
Z-преобразования либо с помощью алгоритма свертки (по выбору студента).
Сделать выводы о сравнении методов синтеза по трудоемкости, сложности конечного результата, о физической достоверности полученной формы отклика в реальных условиях прохождения дискретного сигнала через синтезированную цепь.

Задание на вторую часть курсовой работы Вариант II

Синтезировать заданный шифром N₇N₈ цифровой фильтр с бесконечной (БИХ) или конечной (КИХ) импульсной характеристикой требуемого назначения: фильтр нижних частот (ФНЧ), фильтр верхних частот (ФВЧ), полосовой фильтр (ПФ) или режекторный фильтр (РФ).

Метод синтеза цифрового фильтра, тип аппроксимации частотной характеристики (АЧХ) и наименование оконной функции также заданы шифром N₇N₈.

Параметры затухания А_П и А_З, характеризующие неравномерность АЧХ цифровых фильтров и нормированные граничные частоты полос пропускания

и заграждения

заданы шифром N₉N₁₀.

Рассчитать частотные (амплитудно-частотную и фазочастотную) характеристики синтезированного цифрового фильтра.
Рассчитать временные (импульсную и переходную) характеристики синтезированного фильтра.
Определить вид дискретного сигнала на выходе фильтра при воздействии на его вход последовательности отсчетов заданного входного сигнала x(t).

Руководитель проекта

(Ф.И.О., должность, место работы)

Задание принял к исполнению

(дата, подпись студента)
СОДЕРЖАНИЕ

Введение 8

1Спектральный анализ аналогового сигнала 9

1.1Исходные данные 9

1.2Расчет спектральной плотности аналогового сигнала 10

1.3Расчет коэффициентов комплексного ряда Фурье 15

1.4Восстановление сигнала усеченным рядом Фурье 18

2Дискретизация аналогового сигнала 20

2.1Расчет параметров дискретизации 20

2.2Расчет спектральной плотности дискретного сигнала 20

2.3Расчет спектра комплексных коэффициентов ДПФ 24

3Восстановление аналогового сигнала 26

3.1Восстановление с помощью теоремы Котельникова 26

3.2Восстановление с помощью тригонометрического ряда Фурье 26

4Анализ линейной электрической цепи 28

4.1Исходные данные 28

4.2Определение передаточной функции цепи 28

4.3Построение частотных характеристик аналогового фильтра 29

4.4Определение импульсной характеристики аналогового фильтра 30

5Синтез цифрового фильтра 32

5.1Синтез цифрового фильтра методом инвариантности импульсной характеристики 32

5.2Синтез цифрового фильтра методом билинейного Z-преобразования 38

5.3Расчет отклика РЦФ на дискретный сигнал 40

Заключение 42

Список использованных источников 43

Введение

Целью данной курсовой работы является практическое освоение методов анализа аналоговых и дискретных сигналов во временной и частотной областях, а также расчет цифровых фильтров на примере решения конкретной задачи.

Применение в радиоэлектронике цифровой обработки сигналов позволяет решать задачи, которые невозможно осуществить аналоговыми методами. Также при синтезе в цифровой форме можно достичь лучших характеристик аналоговых устройств-прототипов.

Курсовая работа состоит из двух частей.

Первая часть представляет собой спектральный анализ аналогового сигнала, его дискретизацию и спектральный анализ дискретного сигнала.

Вторая часть содержит синтез цифровых фильтров.

Спектральный анализ аналогового сигнала
1. Исходные данные

Временные интервалы, характеризующие исходный аналоговый сигнал, приведены в таблице 1.1.

Таблица 1.1

Интервал описания фрагмента сигнала t₁, мкс	Интервал описания фрагмента сигнала t₂, мкс	Период описания сигнала, Т_ОС, мкс
70	105	245

Входное напряжение примем равным Е=10 В;

Циклическая частота сигнала.

рад/с.

Временное представление исходного аналогового сигнала сложной формы приведено на рисунке 1.1.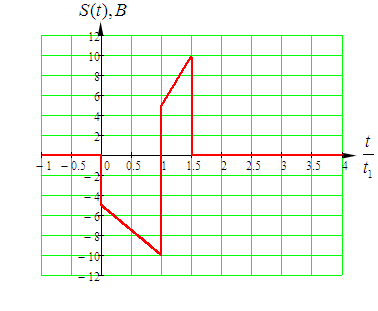

Рисунок 1.1 – Временное представление аналогового сигнала сложной формы (время нормировано относительно t₁₎

Расчет спектральной плотности аналогового сигнала

Для упрощения расчета спектральной плотности мощности с помощью преобразования Лапласа исходя из временного представления сигнала (рисунок 1.1), разложим сигнал на типовые составляющие, включающиеся в определенный момент времени. При разложении используем единичную функцию включения (t) [1].

Сигнал можно разложить на следующие типовые составляющие: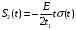

;

.

Исходный аналоговый сигнал представляет собой сумму типовых составляющих

, (1.1)

Временное представление типовых составляющих исходного аналогового сигнала приведено на рисунке 1.2.

Рисунок 1.2 – Временное представление типовых составляющих аналогового сигнала (время нормировано относительно t₁₎
Для расчета спектральной плотности аналогового сигнала, применим прямое преобразование Лапласа к его типовым составляющим [2]. Изображение типовых составляющих исходного аналогового сигнала: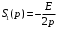

;

.

Изображение исходного аналогового сигнала представляет собой сумму изображений его типовых составляющих

. (1.2)

Сделав замену

в (1.2), получим выражение для спектральной плотности аналогового сигнала

. (1.3)

Спектральная плотность аналогового сигнала является комплексной величиной. Ее модуль называют амплитудно-частотной характеристикой (АЧХ), аргумент – фазочастотной характеристикой (ФЧХ).

График АЧХ исходного аналогового сигнала приведен на рисунке 1.3. График ФЧХ исходного аналогово сигнала приведен на рисунке 1.4.

Рисунок 1.3 – АЧХ аналогового сигнала
(частота нормирована относительно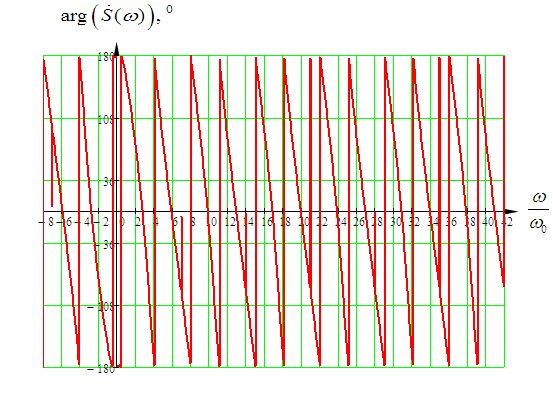

)

Рисунок 1.4 – ФЧХ аналогового сигнала
(частота нормирована относительно

)
ФЧХ имеет большую линейную составляющую, которая мешает увидеть ее значимую часть. Для компенсации линейной составляющей умножим спектральную плотность на

, тогда ФЧХ примет вид, представленный на рисунке 1.5.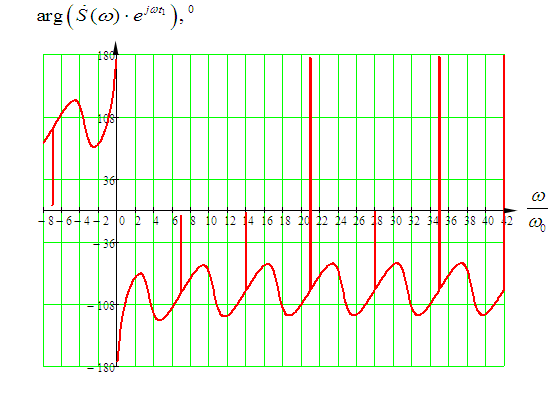

Рисунок 1.5 – ФЧХ аналогового сигнала с компенсированной линейной составляющей (частота нормирована относительно

)

Расчет коэффициентов комплексного ряда Фурье

Для восстановления аналогового сигнала с помощью комплексного ряда Фурье необходимо найти его комплексные коэффициенты. Расчет коэффициентов комплексного ряда Фурье, описывающего исходный аналоговый сигнал, произведем путем дискретизации его спектральной плотности [2]

. (1.4)

Спектр коэффициентов комплексного ряда Фурье приведен на рисунке 1.6.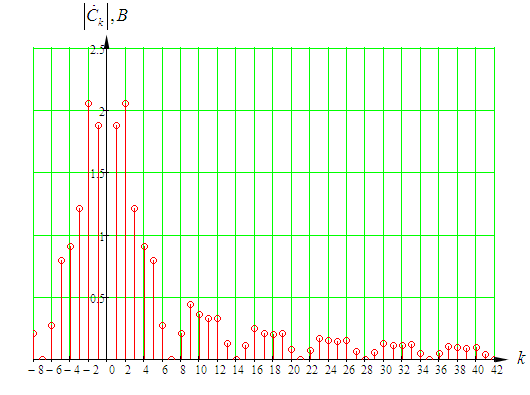

Рисунок 1.6 – Спектр коэффициентов комплексного ряда Фурье
Определим постоянную составляющую исходного аналогового сигнала.

В. (1.5)

Спектр фаз коэффициентов комплексного ряда Фурье приведен на рисунке 1.7. Из рисунка 1.7 видно, что симметричные относительно начала координат коэффициенты являются комплексно-сопряженными.

Рисунок 1.7 – Спектр фаз коэффициентов комплексного ряда Фурье
Для ограничения сигнала, необходимо задаться пороговым критерием. Так как наибольшей энергией обладает вторая гармоника, порог определим как одну десятую часть от ее амплитуды.

На рисунке 1.8 изображен спектр коэффициентов комплексного ряда Фурье. Прямая линия, параллельная частотной оси, определяется пороговым критерием S_ПОР=0,205 B.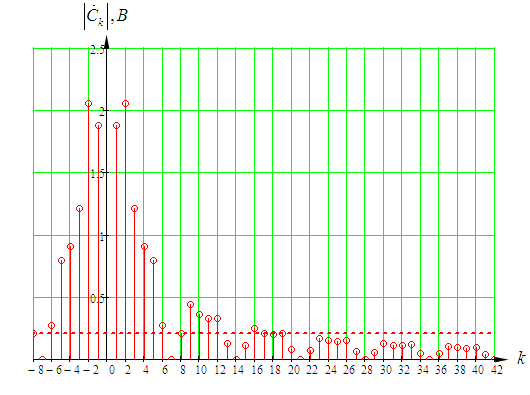

Рисунок 1.8 – Определение ширины спектра аналогового сигнала
Из рисунка 1.8 видно, что последним коэффициентом с амплитудой, превышающей порог, является девятнадцатый коэффициент. Сигнал будем восстанавливать по двадцати гармоникам.

Максимальная частота спектра

рад/с.

Восстановление сигнала усеченным рядом Фурье

Восстановленный сигнал определяется по формуле [1]

. (1.6)

Временное представление восстановленного сигнала приведено на рисунке 1.9.

Рисунок 1.9 – Временное представление восстановленного сигнала
Восстановленный сигнал имеет периодический, пульсирующий характер. Периодизация произошла из-за дискретизации спектральной плотности в частотной области. Пульсации восстановленного сигнала объясняются ограниченной двадцатью гармониками шириной спектра сигнала.

Дискретизация аналогового сигнала
1. Расчет параметров дискретизации

Количество степеней свободы рассчитывается по формуле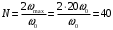

. (2.1)

Выберем N=42.

Интервал дискретизации рассчитывается по формуле

с=6,125 мкс. (2.2)

Расчет спектральной плотности дискретного сигнала

Как это было сделано при анализе аналогового сигнала, для упрощения расчета спектральной плотности мощности с помощью
Z-преобразования, разложим дискретный сигнал на типовые составляющие. При разложении используем единичную функцию включения _n.

Типовые составляющие дискретного сигнала: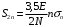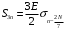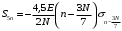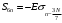

;

.

Дискретный сигнал равен сумме его типовых составляющих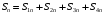

. (2.3)

Графическое представление типовых составляющих дискретного сигнала приведено на рисунке 2.1. Графическое представление дискретного сигнала приведено на рисунке 2.2.

Рисунок 2.1 – Типовые составляющие дискретного сигнала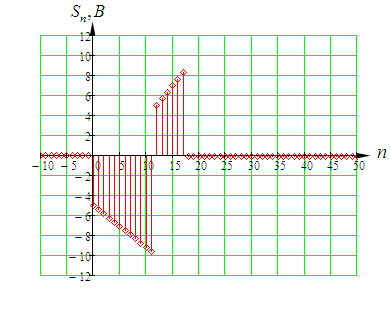

Рисунок 2.2 – Дискретный сигнал

Для расчета спектральной плотности дискретного сигнала, применим к нему прямое Z-преобразование [2]:

. (2.4)

Z-образы типовых составляющих дискретного сигнала: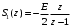

;

.

Для определения спектральной плотности дискретного сигнала, произведем замену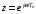

в Z-образах типовых составляющих дискретного сигнала и просуммируем составляющие спектра.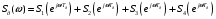

. (2.5)

АЧХ дискретного сигнала приведена на рисунке 2.3.

Из графика (рисунок 2.3) видно, что АЧХ претерпела периодизацию. Это произошло вследствие дискретизации исходного сигнала во времени.

ФЧХ дискретного сигнала приведена на рисунке 2.4. Как и в аналоговом сигнале, скомпенсируем с помощью теоремы сдвига линейную составляющую ФЧХ (рисунок 2.5).

Рисунок 2.3 – АЧХ дискретного сигнала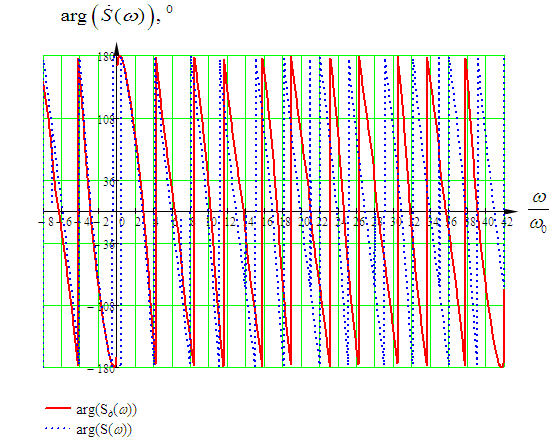

Рисунок 2.4 – ФЧХ дискретного сигнала

Рисунок 2.5 – ФЧХ дискретного сигнала с компенсированной линейной составляющей

Расчет спектра комплексных коэффициентов ДПФ

Для расчета дискретного представления сигнала в частотной области, применим прямое дискретное преобразование Лапласа [1]

. (2.6)

График спектра модулей комплексных коэффициентов ДПФ приведен на рисунке 2.6. График спектра фаз комплексных коэффициентов ДПФ приведен на рисунке 2.7.

Комплексные коэффициенты, симметричны относительно начала координат, являются комплексно-сопряженными.

Рисунок 2.6 – Спектр модулей комплексных коэффициентов ДПФ

Рисунок 2.7 – Спектр фаз комплексных коэффициентов ДПФ

Восстановление аналогового сигнала
1. Восстановление с помощью теоремы Котельникова

С помощью теоремы Котельникова сигнал восстанавливается из простых составляющих с разными весами и сдвигами во времени [1]:

(3.1)

Временное представление сигнала, восстановленного с помощью теоремы Котельникова, приведено на рисунке 3.1.

Рисунок 3.1 – Сигнал, восстановленный с помощью теоремы Котельникова

Восстановление с помощью тригонометрического ряда Фурье

Восстановление по Фурье определяется следующей формулой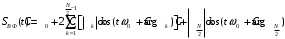

. (3.2)

Временное представление сигнала, восстановленного с помощью тригонометрического ряда Фурье, приведено на рисунке 3.2.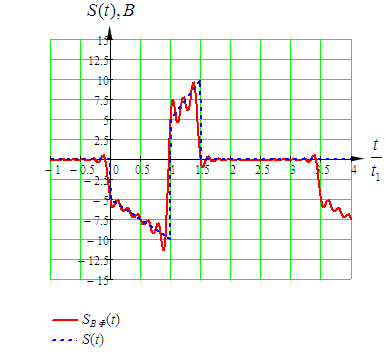

Рисунок 3.2 – Сигнал, восстановленный с помощью тригонометрического ряда Фурье

Анализ линейной электрической цепи
1. Исходные данные

Схема аналоговой электрической цепи-прототипа приведена на рисунке 4.1.

Рисунок 4.1 – Схема заданного фильтра-прототипа
Соотношение между постоянной времени цепи и интервалом описания фрагмента сигнала t₁:

или

. (4.1)

Определение передаточной функции цепи

Операторная передаточная функция по напряжению равна отношению выходного и входного сопротивлений четырехполюсника.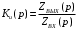

.

Операторные входное и выходное сопротивления равны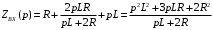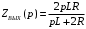

.

Передаточная функция по напряжению равна

.

С учетом (4.1) получим

. (4.2)

Построение частотных характеристик аналогового фильтра

Заменяя в передаточной функции р на j, получим выражение для комплексной передаточной функции аналогового фильтра-прототипа.

. (4.3)

График АЧХ передаточной функции приведен на рисунке 4.2.

Рисунок 4.2 – АЧХ аналогового фильтра-прототипа
Из рисунка 4.2 видно, что аналоговый фильтр-прототип является полосно пропускающим фильтром.

По порогу

определим максимальную частоту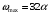

(рисунок 4.3).

Рисунок 4.3 – График зависимости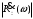

Определение импульсной характеристики аналогового фильтра

Импульсную характеристику цепи определим при помощи обратного преобразования Лапласа от передаточной функции [1].

. (4.4)

Операторная передаточная функция аналогового фильтра

.

Корни знаменателя

.

Операторная передаточная функция аналогового фильтра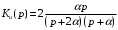

.

В соответствии с (4.4), импульсная характеристика аналоговой цепи

.

Импульсная характеристика аналоговой цепи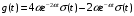

. (4.5)

График нормированной импульсной характеристики приведен на рисунке 4.4.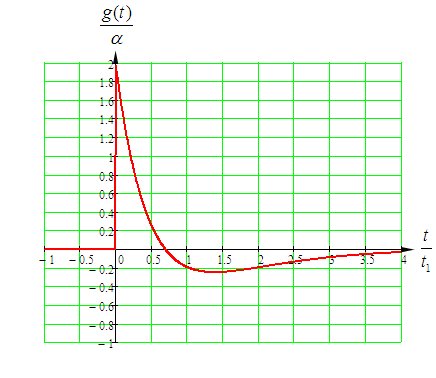

Рисунок 4.5 – Импульсная характеристика аналогового фильтра-прототипа

Синтез цифрового фильтра
1. Синтез цифрового фильтра методом инвариантности импульсной характеристики

Импульсная характеристика аналогового фильтра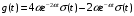

.

Интервал дискретизации рассчитывается по формуле [2]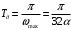

. (5.1)

Для дискретизации импульсной характеристики необходимо сделать замену непрерывного аргумента t на nT_д и провести нормировку полученного выражения относительно T_д.

.

График дискретной импульсной характеристики фильтра приведен на рисунке 5.1.

Рисунок 5.1 – Дискретная импульсная характеристика цепи
Отсчеты импульсной характеристики приведены в таблице 5.1.

Таблица 5.1 – Отсчеты импульсной характеристики цепи

n	1	2	3	4	5	6	7	8	9	10
g_n	0,145	0,105	0,073	0,047	0,028	0,013	0,001	-0,007	-0,013	-0,018

Ограничиваем импульсную характеристику шестью отсчетами по уровню 0,1.

Тогда системная функция трансверсального цифрового фильтра (ТЦФ) определяется по формуле [2]

. (5.2)

Структурная схема ТЦФ приведена на рисунке 5.2.

Рисунок 5.2 – Структурная схема ТЦФ
Частотные характеристики ТЦФ получаются из системной функции, путем замены z=e^j^^T^д.

Графики АЧХ и ФЧХ трансверсального цифрового фильтра приведены на рисунке 5.3 и рисунке 5.4 соответственно.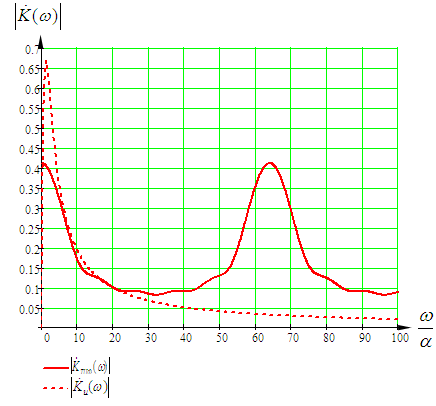

Рисунок 5.3 – АЧХ трансверсального цифрового фильтра

Рисунок 5.4 – ФЧХ трансверсального цифрового фильтра
Системная функция рекурсивного цифрового (РЦФ) фильтра с бесконечной импульсной характеристикой (БИХ) определяется формулой [1]

. (5.3)

Для получения системной функции необходимо подставить дискретную импульсную характеристику и свернуть бесконечные геометрические прогрессии по формуле

,

где S – сумма бесконечно убывающей геометрической прогрессии;

b₁ – первый член прогрессии;

q – знаменатель прогрессии.

Системная функция РЦФ

.

Канонический вид выражения

. (5.4)

На основе выражения (5.4) получается алгоритм работы РЦФ

.

Структурная схема РЦФ приведена на рисунке 5.5.

Рисунок 5.5 – Структурная схема РЦФ
Частотные характеристики РЦФ получаются из системной функции, путем замены z=e^j^^T^д.

Графики АЧХ и ФЧХ рекурсивного цифрового фильтра приведены на рисунке 5.6 и рисунке 5.7 соответственно.

Рисунок 5.6 – АЧХ рекурсивного цифрового фильтра

Рисунок 5.6 – ФЧХ рекурсивного цифрового фильтра

Синтез цифрового фильтра методом билинейного Z-преобразования

Переход к системной функции рекурсивного фильтра при синтезе методом билинейного Z-преобразования осуществляется путем замены в передаточной функции фильтра-прототипа [1]

(5.5)

Путем подстановки (5.5) в (4.2) и необходимых преобразований, получим системную функцию рекурсивного фильтра в каноническом виде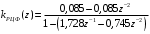

. (5.6)

На основе этого выражения получается алгоритм работы

.

Структурная схема РЦФ приведена на рисунке 5.7.

Рисунок 5.7 – Структурная схема РЦФ
Частотные характеристики РЦФ получаются из системной функции, путем замены z=e^j^^T^д.

Графики АЧХ и ФЧХ рекурсивного цифрового фильтра приведены на рисунке 5.8 и рисунке 5.9 соответственно.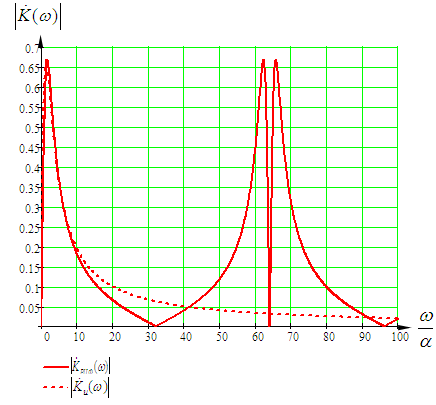

Рисунок 5.8 – АЧХ рекурсивного цифрового фильтра

Рисунок 5.9 – ФЧХ рекурсивного цифрового фильтра

Расчет отклика РЦФ на дискретный сигнал

Отклик на выходе цифрового фильтра можно получить при помощи применения дискретной свертки, которая задается следующим соотношением [1]:

. (5.7)

Для расчета отклика цепи, рассчитаем импульсную характеристику РЦФ.

Системная функция для расчета импульсной характеристики

.

Корни знаменателя

.

Системная функция цифрового фильтра

.

Импульсная характеристика РЦФ рассчитывается при помощи обратного преобразования Лапласа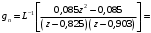

.

Импульсная характеристика РЦФ

.

Отклик цепи на воздействие дискретного сигнала, рассчитанный по (5.7), приведен на рисунке 5.10.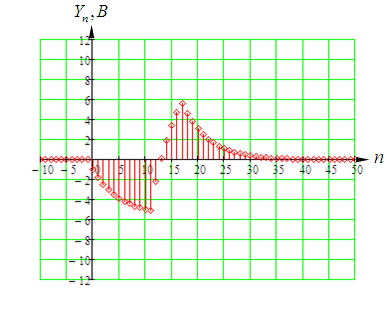

Рисунок 5.10 – Отклик цепи на дискретный сигнал
Из рисунка 5.10 видно, что цифровой фильтр интегрирует входной дискретный сигнал. Значит, расчет проведен правильно.

Заключение

В процессе выполнения работы был проведен спектральный анализ аналогового сигнала, его дискретизация и спектральный анализ дискретного сигнала.

Спектр дискретного сигнала в области нижних частот повторяет спектр аналогового сигнала, но в отличие от аналогового, спектр дискретного сигнала с повышением частоты периодически повторяется.

Далее было проведено восстановление аналогового сигнала из дискретного при помощи теоремы Котельникова и при помощи тригонометрического ряда Фурье. При восстановлении сигнала при помощи тригонометрического ряда Фурье происходит его периодизация.

Вторая часть работы посвящена синтезу цифровых фильтров на основуе временных и частотных характеристик аналогового фильтра-прототипа различными методами.

Самая близкая форма АЧХ цифрового фильтра к форме АЧХ аналогового фильтра-прототипа в рабочей области частот получена при синтезе рекурсивного цифрового фильтра методом билинейного
Z-преобразования.

Список использованных источников

1 Каратаева Н. А. Радиотехнические цепи и сигналы. Дискретная обработка сигналов и цифровая фильтрация: Учебное пособие. – Томск: ТУСУР, 2012. – 257 с.

2 Каратаева Н. А. Радиотехнические цепи и сигналы. Дискретная обработка сигналов и цифровая фильтрация: методические указания по выполнению курсовой работы. – Томск: ФДО, ТУСУР, 2018. – 79 с.

3 Баскаков С.И. Радиотехнические цепи и сигналы. М.: Высш. школа, 2005. – 462с.

4 Образовательный стандарт вуза ОС ТУСУР 01-2013. Работы студенческие по направлениям подготовки и специальностям технического профиля. Общие требования и правила оформления (Утвержден и введен в действие Приказом ректора ТУСУР от 03.12.2013 г. №14103) [Электронный ресурс]: – Режим доступа: https://regulations.tusur.ru/documents/70 (дата обращения 04.04.2020).