Курсовая работа по теории вероятности. Пояснительная записка к курсовой работе По теме Статистическое исследование случайной величины

• Название: Пояснительная записка к курсовой работе По теме Статистическое исследование случайной величины
• Анкор: Курсовая работа по теории вероятности
• Дата: 15.06.2022
• Размер: 0.75 Mb.
• Имя файла: Kursovaya_Zaslavskii_774.docx
• Тип: Пояснительная записка; #592185
• страница: 3 из 5

Глава 2.

Выборка моментов отказа компрессоров КАМАЗ 53205 (в часах)

Исходные данные по выборке (100 чисел задания на работу сведены в табл. 2.1).
Моменты отказов компрессоров Таблица 2.1

1. 
   Графическое представление выборки
   

Размах выборки R и объём выборки n

Просматривая все элементы табл. 2.1, находим X_min = 14 и X_max = 795.

Тогда размах выборки R=X_max - X_min = 781. По условия задачи объём выборки n = 100.

1. 
   Разбиваем значения выборки на 10 интервалов (для упрощения расчётов пологая их длины одинаковыми и равными ∆ = R/10 = 781/10 = 78,1; n_инт = 10). Результаты сведены в табл. 2.2
   

Интервалы Таблица 2.2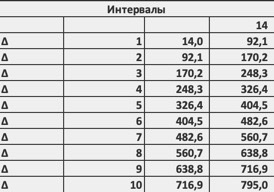

2. 
   Строим вариационный ряд выборки, для чего результаты выборки следует упорядочить (отсортировать) по возрастанию. В табл. 2.3 вариационный ряд приведён во втором столбце. Для удобства расчётов во втором столбце приведены интервалы ∆i и их границы.
   

Далее находим количество n_i (частоты) вариант и количество относительных частот wi, попавших на интервалы ∆i и среднее значение x_iср = (∑x_i)/ n_i случайной величины на соответствующем интервале. И по найденным значениям n_i и x_iср дополняем таблицу, где проводим подсчёт нужных статистических параметров выборки.

Статистическое распределение выборки Таблица 2.3

Статистическое распределение выборки
N	Δi	Варианты (xi)	Частоты (ni)	относительная частота (wi)	xi ср	плотность частоты (ni/h)	плотность относительной частоты (wi/h)
1	[14,0-92,1)	14	28	0,28	51,429	0,35851	0,0036
		16
		23
		23
		33
		34
		35
		35
		37
		37
		37
		41
		44
		47
		51
		59
		61
		67
		67
		68
		69
		71
		71
		74
		76
		78
		83
		89
2	[92,1-170,2)	97	24	0,24	128,83	0,30730	0,0031
		104
		106
		109
		111
		112
		117
		118
		119
		120
		120
		127
		128
		130
		132
		136
		143
		143
		145
		147
		148
		157
		161
		162
3	[170,2-248,3)	174	23	0,23	206,61	0,29449	0,0029
		178
		180
		181
		182
		182
		190
		190
		191
		194
		197
		204
		206
		219
		219
		224
		226
		226
		226
		234
		240
		244
		245
4	[248,3-326,4)	251	8	0,08	276,5	0,10243	0,0010
		254
		257
		258
		281
		296
		296
		319
5	[326,4-404,5)	328	11	0,11	358,64	0,14085	0,0014
		331
		341
		345
		346
		350
		361
		377
		385
		389
		392
6	[404,5-482,6)	406	2	0,02	421,5	0,02561	0,0003
		437
7	[482,6-560,7)	535	1	0,01	535	0,01280	0,0001
8	[560,7-638,8)	628	1	0,01	628	0,01280	0,0001
9	[638,8-716,9)	640	1	0,01	640	0,01280	0,0001
10	[716,9-795,0]	795	1	0,01	795	0,01280	0,0001

Проводим подсчёты для эмпирической функции распределения вероятности согласно формуле
F_i* = 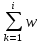_k , I = 1, 2, 3, … , 10.
Таблица 2.4

эмпирическая функция F*(x)
0	x⩽51,43
0,28	51,4⩽128,8
0,52	128,8⩽206,6
0,75	206,6⩽276,5
0,83	276,5⩽358,6
0,94	358,6⩽421,5
0,96	421,5⩽535
0,97	535⩽628
0,98	628⩽640
0,99	640⩽795
1	x>795

Строим график эмпирической функции распределения вероятностей F*(x).
График эмпирической функции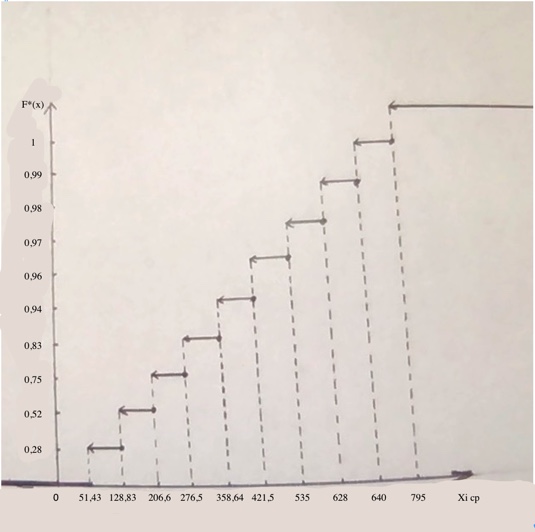