Курсовая работа по теории вероятности. Пояснительная записка к курсовой работе По теме Статистическое исследование случайной величины
 Скачать 0.75 Mb. Скачать 0.75 Mb.
|
|
Проверка на нормальное распределение Таблица 2.9 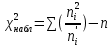 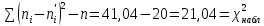 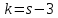 – число степеней свободы – число степеней свободы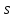 – число интервалов – число интервалов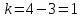 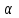 = 0.05 – уровень значимости (по условию) = 0.05 – уровень значимости (по условию)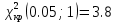 – критическая точка правосторонней критической области (Приложение №5) – критическая точка правосторонней критической области (Приложение №5)Вывод: т.к. 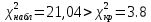 не принимаем гипотезу о нормальном распределение генеральной совокупности т.е. мпирические и теоретические частоты различаются значительно. Это означает что данные наблюдений не согласуются с гипотезой о нормальном распредилении выборки (n=20) т.к. выборка является не репрезентативной, будем проверять ее на n=100 не принимаем гипотезу о нормальном распределение генеральной совокупности т.е. мпирические и теоретические частоты различаются значительно. Это означает что данные наблюдений не согласуются с гипотезой о нормальном распредилении выборки (n=20) т.к. выборка является не репрезентативной, будем проверять ее на n=100Проверка гипотезы о показательном распределении генеральной совокупности. Для того чтобы при уровне значимости а проверить гипотезу о том, что непрерывная случайная величина распределена по показательному закону, надо: 1. Найти по заданному эмпирическому распределению выборочную среднюю хcp. Для этого находят середину i-го интервала xcπ = (xi+xi+1)/2, составляют последовательность равноотстоящих вариант и соответствующих им частот. 2. Принять в качестве оценки параметра Х показательного распределения величину, обратную выборочной средней: λ = 1 / X 3. Найти вероятности попадания X в частичные интервалы (xi,xi+1) по формуле: Pi = P(xi < X < xi+1) = e-λxi - e-λxi+1 4. Вычислить теоретические частоты: ni = n • Pi 5. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы k = s-2, где s - число первоначальных интервалов выборки; если же было произведено объединение малочисленных частот, следовательно, и самих интервалов, то s - число интервалов, оставшихся после объединения. Среднее значение равно 188,82. Следовательно, параметр λ = 1 / 188,82 = 0.0053 Таким образом, плотность предполагаемого показательного распределения имеет вид: f(x) = 0.0053e-0.0053x, x ≥ 0 Найдем вероятности попадания 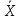 в каждый из интервалов по формуле: в каждый из интервалов по формуле:Pi = P(xi < X < xi+1) = e-λxi - e-λxi+1 P1 = (14 < X < 92,1) = 0,314540882 , ni = 100 • 0.3145 = 31.45 P2 = (92,1 < X < 170,2) = 0,207990545 , ni = 100 • 0.2080 = 20.80 P3 = (170,2 < X < 248,3) = 0,137534003 , ni = 100 • 0.1375 = 13.75 P4 = (248,3 < X < 326,4) = 0,090944528 , ni = 100 • 0.0909 = 9.09 P5 = (326,4 < X < 404,5) = 0,060137181 , ni = 100 • 0.0613 = 6.13 P6 = (404,5 < X < 482,6) = 0,039765785 , ni = 100 • 0.0398 = 3.98 P7 = (482,6 < X < 560,7) = 0,026295174 , ni = 100 • 0.0263 = 2.63 P8 = (560,7 < X < 638,8) = 0,017387716 , ni = 100 • 0.0174 = 1.74 P9 = (638,8 < X < 716,9) = 0,011497649 , ni = 100 • 0.0115 = 1.15 P10 = (716,9 < X < 795) = 0,007602834 , ni = 100 • 0.0076 = 0.76 Проверка на показательное распределение Таблица 2.10
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы. Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞). Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=1 (параметр λ). Kkp(8,0.05) = 15.5; Kнабл = 13.756 Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл < Kkp, поэтому нет оснований отвергать основную гипотезу. Справедливо предположение о том, что данные выборки имеют показательный закон. Выводы: Каждое значение ряда отличается от среднего значения 188,82 в среднем на 143.4. Среднее значение существенно отличается от медианы, что свидетельствует о распределении выборки отличного от нормального. Вывод по главе: с помощью методов математической статистики (графическое представление выборки, точечные оценки, интервальные оценки, критерий согласия Пирсона, критерий Стьюдента и хиквадрат) мы убедились в верности выбранной (нулевой) гипотезы о показательном распределении. Статистические данные распределены по показательному закону. Заключение В ходе выполнения курсовой работы было произведено статистическое исследование случайной величины. В расчетной части были решены четыре задания, для освоения методики и технологии проведения статистических расчетов. В курсовой работе проведена группировка исходной выборки и построены: полигон, гистограмма, эмпирическая функция распределения для выборочных данных. В ходе статистического исследования случайной величины были вычислены точечные оценки параметров распределения (среднее значение выборки, дисперсия, выборочное среднее квадратическое отклонение другие показатели). В результате выполненных расчетов подтвердилась гипотеза о том, что данные выборки имеют показательное распределение. Список использованной литературы: Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов/В.Е. Гмурман. – 9-е изд., стер. – М.: Высш. шк., 2004. 154-309 с.: ил. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В.Е. Гмурман. – 9-е изд., стер. – М.: Высш. шк., 2003. С81-209.: ил. Ряд. Заславский Д.Е. Конспект лекций по дисциплине «Теория вероятностей и математическая статистика» 2022. С 14-20. 4. Серебряный М.С. Руководство к решению задач по теории вероятностей и математической статистике. Учебное пособие. – Новогорск, 2001. 5. В.Д.Фролов «Учебно - методическое пособие по курсовой работе» 2006г |
