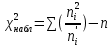Курсовая работа по теории вероятности. Пояснительная записка к курсовой работе По теме Статистическое исследование случайной величины
 Скачать 0.75 Mb.
|
|
Рис 2.1. Эмпирическая функция распределения Строим график полигона частот. 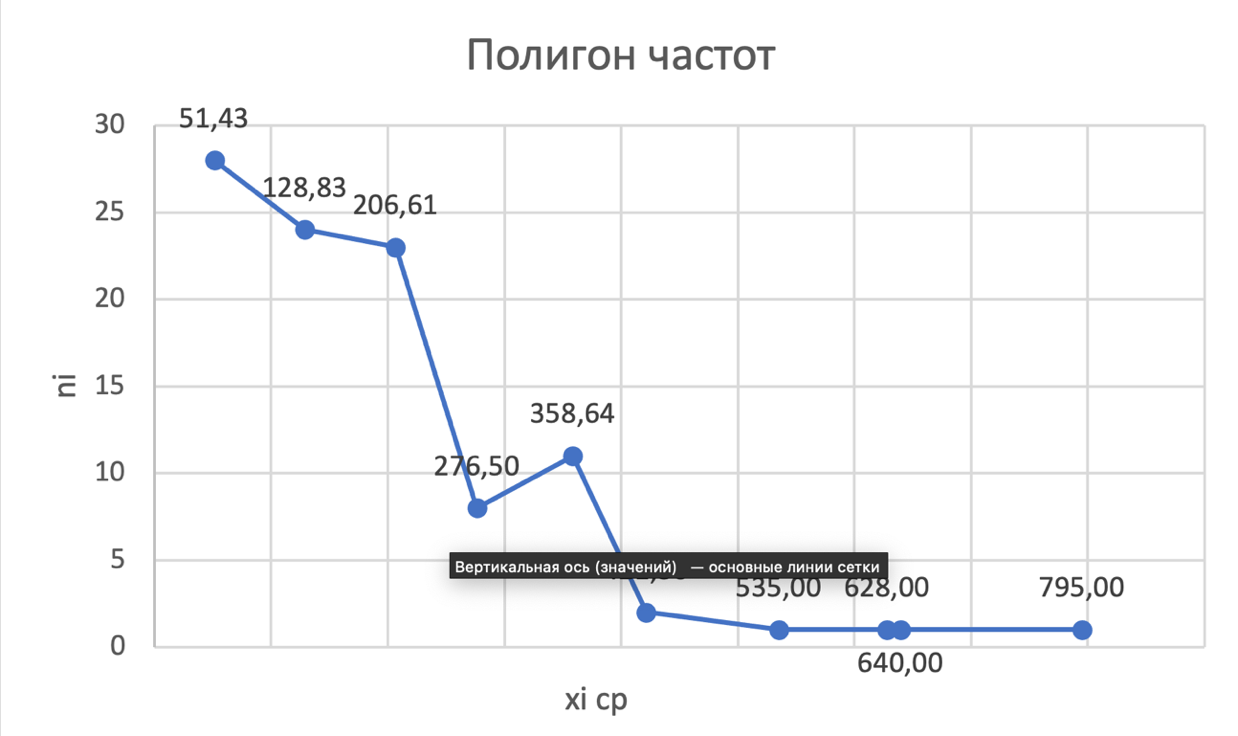 Рис 2.2. Полигон частот Строим график полигона относи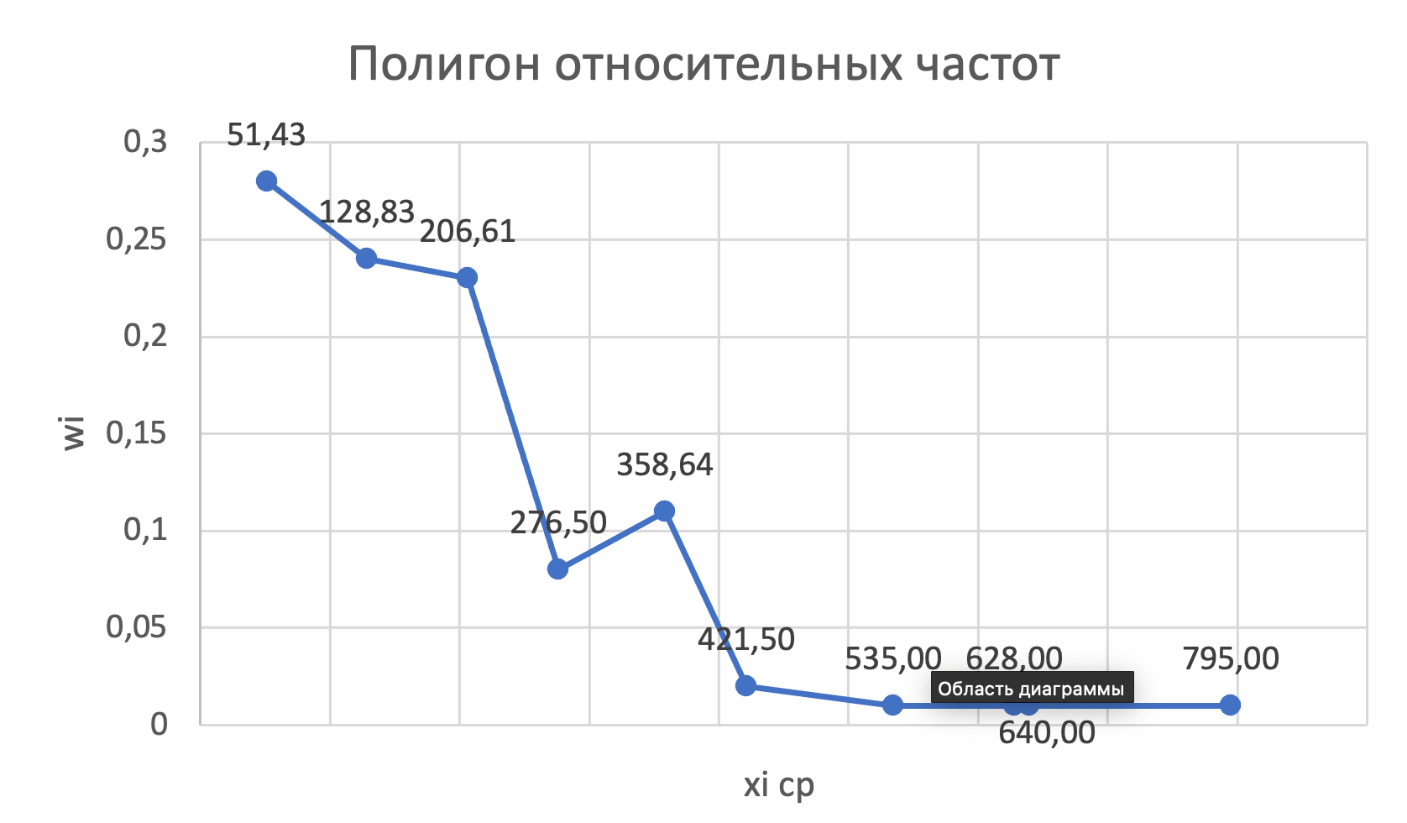тельных частот.  Рис 2.3. Полигон относительных частот Строим гистограмму приведённых частот. 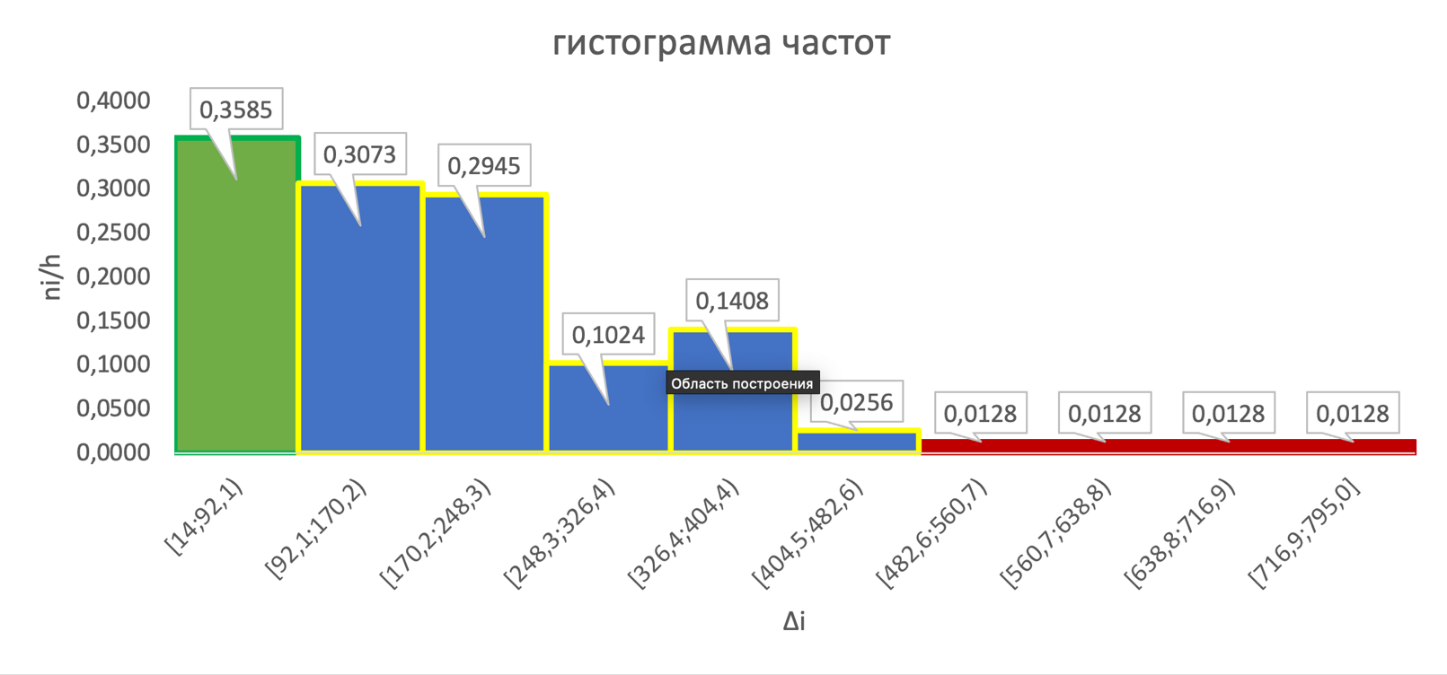 Рис. 2.4 Гистограмма частот Строим гистограмму относительных частот. 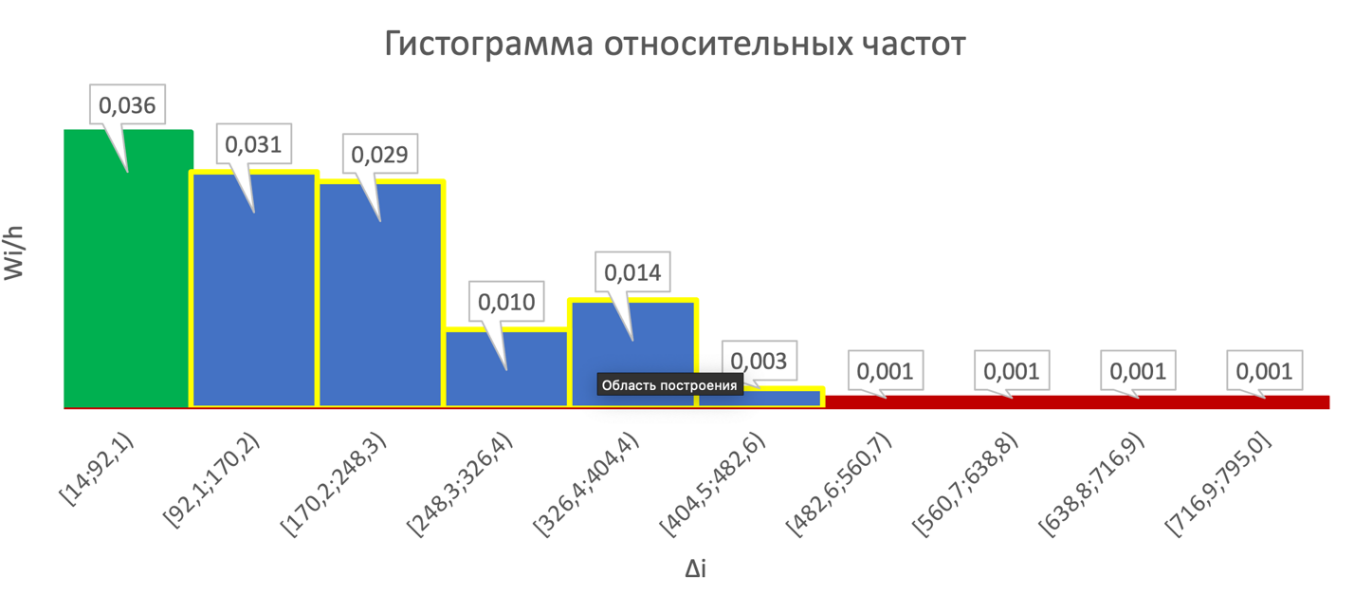 Рис. 2.5 Гистограмма относительных частот Вывод: Исходя из полученных графиков мы можем выдвинуть гипотезу что H0-показательное распределение. 2.2. Точечные оценки параметров выборки. Значения для точечных оценок параметров находим по формулам для данных представленных в табл. 2.3. Выборочное среднее 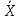 в= (∑nixi) / n. Выборочная дисперсия Dв= (∑ ni(xi- 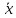 в)2) /n.Выборочное среднее квадратичное отклонение Ϭв=√Dв. Исправленная выборочная дисперсия S2=n*Dв/(n-1). Исправленное выборочное среднее квадратичное отклонение S=√s2
2.3. Интервальны оценки параметров нормального распределения случайной величины Данные для разделов III и IV берём из исходных данных (табл. 2.1), ограничившись первыми 20 числами (табл. 2.6). В табл. 2.6 второй столбец это первые 20 чисел выборки, заданной в табл. 2.1, третий столбец получен упорядочением выборочных данных, записанных во втором столбце. Вариационный ряд Таблица 2.6
Найдём доверительный интервал для оценки математического ожиданияпри неизвестном среднем квадратичном отклонении с надёжностью 0,95. Согласно формуле (10) при объёме выборки n = 20 и надёжность γ = 0,95, нужно найти выборочное среднее хв и исправное квадратичное отклонение s Хв= (∑xi) / n = 208,45 S2= (∑ (xi-xв)2 ) / (n-1) = 20177,92677 S=√s2 = 142,0490294 По справочным таблицам для n = 20 и γ = 0,95 находим tγ: tγ = 2,093. Тогда доверительный интервал для математического ожидания, а равен xв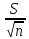-tγ  < a < xв+tγ 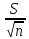или 141,97< a <274,93; Найдём доверительный интервал для оценки среднего квадратичного отклоненияϬ с надёжностью 0,95. Согласно формуле (11) при объёме выборки n = 20 и надёжность γ = 0,95, S(1-q) <Ϭ< S(1+q) (q<1) Значение q находим из справочных таблиц : q = 0,37. Тогда доверительный интервал для среднего квадратичного отклонения Ϭ равен 89,4908886< Ϭ < 194,6071703 Вывод: При оценке математического ожидания при n= 20 мат. ожидание при n= 100 попадает в доверительный интервал и среднее квадратичное отклонение при n=100 попадает. IV. Проверка статистических гипотез. Используем данные выборки из предыдущего пункта (вариационный ряд в третьем столбце табл. 2.6). 2.4. Проверить гипотезу о нормальном распределении генеральной совокупности. При уровне значимости 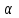 = 0,05. 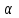В качестве нулевой (основной) гипотезы Н0 примем предположение о нормальном распределении генеральной совокупности при уровне значимости = 0,05.Вычислим выборочную среднюю Хв* и среднее квадратичное отклонение σ*, причём в качестве варианта хi берём середины интервалов xi ср = (xi + xi+1*)/2. Результаты сведены в табл. 2.7. Границы интервалов и их средние значения Таблица 2.7
хв*=(∑ Хi ср*ni*)/20 = 208,45 ; σ*=√(∑ (xi ср*-xв)2ni*)/20)= 136,8; От случайной величины Х перейдём к стандартной случайной величине Z из N(0,1), сдвинув математическое хв в начало координат и пронормировав по σ к единице: zi = (xi ср*-xв*) / σ*; i = 1, 2, 3, 4; при этом полагаем z1 = -∞, a z4 = ∞. Результаты сведены в табл. 2.8 Нахождение интервалов (zi;z(i+1)) Таблица 2.8
Вычислим теоретические частоты в предположении, что Z нормальная случайная величина. ni 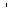 = nPi, где n – объём выборки (в рассматриваемом случае n = 20),Pi = Ф(zi+1) – Ф(zi), вероятность попадания Х на интервал (xi*, xi+1*) или Z на (zi, zi+1), а Ф(zi) – функция Лапласа (её значения определяются по справочным таблицам). Результаты вычисления сведены в табл. 2.9.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
