Курсовая работа по теории вероятности. Пояснительная записка к курсовой работе По теме Статистическое исследование случайной величины

• Название: Пояснительная записка к курсовой работе По теме Статистическое исследование случайной величины
• Анкор: Курсовая работа по теории вероятности
• Дата: 15.06.2022
• Размер: 0.75 Mb.
• Имя файла: Kursovaya_Zaslavskii_774.docx
• Тип: Пояснительная записка; #592185
• страница: 2 из 5

рядовой Лужных Д.С.
Консультант_______________________________________________________
(должность, звание, подпись, ФИО)

«_____»_______________ 2022 г.

рядовой Заславский Д.Е.
Задание получил_____________________________________________________
(должность, звание, подпись, ФИО)
«_____»_______________2022 г.

Курсовая работа
№ п/п	Тема	Целевые установки и разрабатываемые вопросы	Фамилия и инициалы курсанта	Звание, фамилия и инициалы руководителя
	Статистическое исследование случайной величины	1. Графическое представление выборки – помогает выдвинуть нулевую гипотезу 2. Точечные оценки - определяем числовые характеристики параметров распределения 3. интервальные оценки- при малой выборки производят оценку данных 4. Критерий согласия Пирсона- проверяет гипотезу о нормальном распределении 5. Критерий Стьюдента и хи квадрат( 2)- проверяют параметры уже известного распределения.	рядовой Заславский Д.Е.	Доцент к.т.н. Шимитило В.Л.

Заведующий кафедры
(должность, звание, подпись, фамилия)

Аннотация

Представленная курсовая работа состоит из введения, двух глав, заключения, списка литературных источников, вывода и заключения. В первой части работы мы знакомимся с теоретическими основами математической статистики, познакомились с эмпирической функцией, выборочным средним, научились вычислять доверительный интервал для оценки математического ожидания при неизвестном среднем квадратическом отклонении, а так же формулировать нулевую гипотезу о величине генеральной средней (при неизвестной дисперсии) и делать проверку трёх альтернативных гипотез для уровня значимости 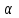= 0,05.

В следующей главе мы практически применяем методы математической статистики для обработки данных, делаем вывод и составляем заключение.

Работа состоит из 27 страницы, содержит 5 литературных источника, 10 таблиц, 5 рисунков.

Данная работа является завершающим этапом в изучении дисциплины «Теория вероятности и математическая статистика».



Содержание

Введение……………………………………………………………………….….8

Теоретическая часть

Глава первая. Теоретические основы математической статистики…………...9

1.1. Эмпирическая функция распределения ………………….…….…………..9

1.2. Выборочное среднее…………………………………………….………......10

1.3. Вычисление доверительного интервала для оценки математического ожидания при неизвестном среднем квадратическом отклонении………..…11

1.4. Формулирование нулевой гипотезы о величине генеральной средней (при неизвестной дисперсии) и проверка трёх альтернативных гипотез для уровня значимости 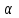= 0,05 ..…………………..……… ……………………………...12

Практическая часть

Глава вторая. Практическое применение методов математической статистики для обработки данных………………………….………………………………..13

2.1. Графическое представление выборки……………………………….….....13 2.1.1. Ранжировка на интервалы………………………………………...….…..13

2.1.2. Вариационный ряд………………………………………………………..13

2.1.3. Статистическое распределение выборки……………………..……..…..14

2.1.4. Функция распределения…………………………………………..….......17

2.1.5. Полигон частот……………………………………………..………..…....18

2.1.6. Полигон относительных частот…………………………..…………..….18

2.1.7. Гистограммы частот…………………………………….…....………..….19

2.1.8. Гистограммы относительных частот……………………….………...…19

2.2. Точечные оценки параметров распределения……………………….……20

2.2.1. Выборочное среднее………………………………….……………..……20

2.2.2. Выборочная дисперсия и выборочное среднее квадратическое отклонение…………………………………………………………………..…...20

2.2.3. Исправленная выборочная дисперсия и исправленное выборочное среднее квадратическое отклонение……………………………………..….….20

2.3. Интервальные оценки параметров нормально распределенной случайной величины…………………………………………………………………...…….20

2.3.1. Доверительный интервал для оценки математического ожидания……21

2.3.2. Доверительный интервал для оценки среднего квадратического отклонения………………………………………….……………………….…...21

2.4. Проверка гипотезы о нормальном распределении генеральной совокупности ………………………………………………………………....….22

2.4.1 Проверка гипотезы о показательном распределении генеральной совокупности ………………………………………………………………...…..23

2.4.2. Определение границ критической области …………...………………...25

Вывод по главе……………………………………………………………….…..25
Заключение……………………………………………………………….……....26

Список использованной литературы……………………………...………....…27



Введение

Использование статистических методов обработки данных стали привычным и широко распространенным аппаратом для инженеров, механиков, а также и специалистов МЧС России. Одним из самых распространённых видов ЧС является ДТП, зачастую они связаны с отказом компрессоров. Сами компрессоры пользуются большой популярностью во многих отраслях народного хозяйства, включая транспортную промышленность, и ценятся за надёжность, высокий коэффициент полезного действия, длительные сроки эксплуатации, так же они играют не маловажную роль в поставки гуманитарного груза и прочих перевозок на КАМАЗах. Однако, они как и все материальное имеют свойство ломаться.

Поэтому данная работа посвящена статистическому анализу моментам отказов компрессоров КАМАЗ53205.

Предметом работы является надежность использования технических средств.

Целью работы заключается в анализе статистических данных для прогнозирования отказа компрессоров, на основе которых будут поставлены задач по противодействию поломкам при помощи сил МЧС России.

Объектом данной работы являются моменты отказов компрессоров КАМАЗ53205.

Используются следующие методы:

1. 
   Графическое представление выборки – помогает выдвинуть нулевую гипотезу.
   
2. 
   Точечные оценки- определяем числовые характеристики параметров распределения.
   
3. 
   Интервальные оценки- при малой выборки производим оценку данных.
   
4. 
   Критерий согласия Пирсона- проверка гипотезы о нормальном распределении.
   
5. 
   Критерий Стьюдента и хиквадрат( ²)- проверяют параметры уже известного распределения.
   

Основной целью данной работы является проверка гипотезы о виде неизвестного распределения моментов отказа компрессоров КАМАЗ53205.

Теоретическая часть

Глава первая.

Теоретические основы математической статистики

1.1 Эмпирическая функция распределения (функция распределения выборки)

Эмпирическая функция распределения – это функция F(x), определяющая для каждого значения X относительную частоту события X <x:
F(x) = Nx/N, (1.1)
Где Nx – число вариантов, меньших х; N- объём выборки.

Эмпирическая функция обладает следующими свойствами:

Свойство 1. Значения эмпирической функции принадлежат отрезку [0;1].

Свойство 2. F(х) – неубывающая функция.

Свойство 3. Если x1- наименьшая варианта, а xk- наибольшая, то F(x)=0 при х <=x1 и F(x)=1 при х> xk

Пусть известно статистическое распределение частот количественного признака X. Обозначим через 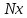  число наблюдений, при которых наблюдалось значение признака, меньшее x и через n – общее число наблюдений. Очевидно, относительная частота события X 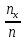равна    и является функцией x. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию F(x), определяющую для каждого значения x относительную частоту события X 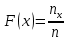. Таким образом, по определению   , где 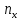  – число вариант, меньших x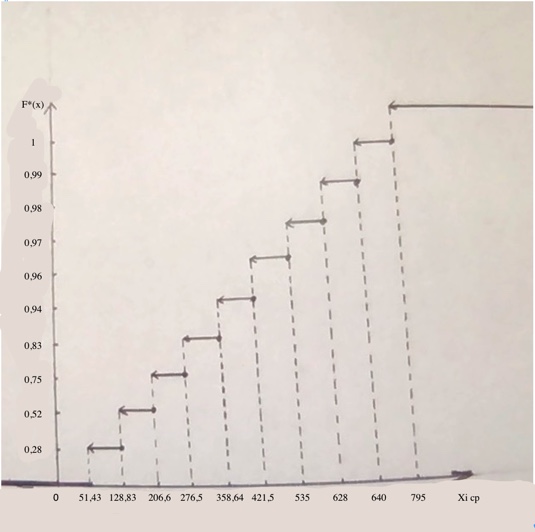


Рис 1.1. Эмпирическая функция распределения
1.2 Выборочное среднее

Выборочное среднее ( 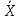_в) – это одна из основных статистик распределения, которая характеризует среднее значение рассматриваемых выборочных данных.

Для нахождения средней выборочной существуют несколько формул, применение которых зависит от того, в каком виде представлены выборочные данные.

Если выборочные данные записаны в виде произвольной последовательности чисел: х₁, х₂, …, х_n, то для нахождения средней выборочной используется обычная формула, называемая формулой простой средней

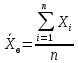(1.6)

Если выборочные данные записаны в виде вариационного дискретного ряда распределения частот, то для нахождения средней выборочной используется формула, называемая формулой взвешенной средней

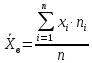(1.8)

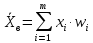(1.9)
Очевидно, что если в вариационном ряде заданы не частоты, а частности, то формула (1.8) примет вид (1.9).

Название формулы, взвешенной средней связано с тем, что частоты n_iчасто называют весами, так как, по сути, они показывают какой вес имеет рассматриваемый вариант во всей совокупности, а сама операция умножения x_in_i называется взвешиванием.

Средняя выборочная является выборочным аналогом математического ожидания случайной величины, хотя эти характеристики имеют и принципиальные отличия. Если сравнить формулу для математического ожидания дискретной случайной величины и формулу (1.8), то внешняя схожесть этих формул очевидна. Однако в формуле для математического ожидания значения случайной величины умножаются на вероятности этих значений, а в формуле (1.9) значения вариант умножаются на относительные частоты этих вариант. В то же время следует отметить, что при определенных условиях, при неограниченном увеличении числа n средняя выборочная сходится по вероятности к математическому ожиданию (теорему Чебышева).


1.3 Вычисление доверительного интервала для оценки математического ожидания при неизвестном среднем квадратическом отклонении.
Пусть произведена выборка из генеральной совокупности, подчиненной закону нормального распределения XN(m;). Это основное предположение математической статистики основано на центральной предельной теореме. Пусть известно генеральное среднее квадратическое отклонение ,но неизвестно математическое ожидание теоретического распределения m (среднее значение).

В таком случае среднее выборочное 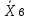 , полученное в ходе эксперимента также будет являться случайной величиной 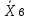m; ). Тогда «нормализованное» отклонение

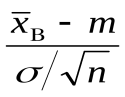(1.10)

– является стандартной нормальной случайной величиной.

Задача состоит в поиске интервальной оценки для m. Построим двусторонний доверительный интервал для m так, чтобы истинное математическое ожидание принадлежало ему с заданной вероятностью (надежностью) .

Установить такой интервал для величины (3.1)– это значит найти максимальное значение этой величины и минимальное , которые являются границам критической области:

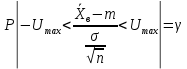(1.11)

Т.к. такая вероятность равна  , то корень этого уравнения можно найти с помощью таблиц функции Лапласа (приложение 1).

Тогда с вероятностью  можно утверждать, что случайная величина 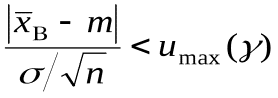 естьточностьоценки, то есть искомое генеральное среднее принадлежит интервалу

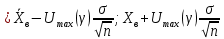(1.12)

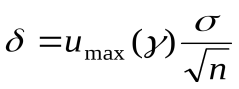(1.13)

1.4 Формулирование нулевой гипотезы о величине генеральной средней (при неизвестной дисперсии) и проверка трёх альтернативных гипотез для уровня значимости 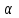= 0,05.
Правило 1: Для того чтобы при заданном уровне значимости α проверить нулевую гипотезу H₀: Ϭ²=Ϭ₀² о равенстве неизвестной генеральной дисперсии Ϭ² гипотетическому значению Ϭ₀² при конкурирующей гипотезе H₁: Ϭ²>Ϭ₀²- наблюдаемое значение критерия :
²_набл=(n-1)s²/ Ϭ₀² (1.14.)
И по таблице критических точек распределения ² , по заданному уровню значимости α и числу степеней свободы k=n-1 найти критическую точку ²_кр(α; k). Если ²_набл< ²_кр – нет оснований отвергать нулевую гипотезу. Если ²_набл> ²_кр-нулевую гипотезу отвергают.
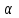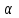Правило 2: При конкурирующей гипотизе H₁: Ϭ²≠Ϭ₀² находят левую ²_{лев. кр.}(1- _{/2; k) и правую} ²_{прав. кр.}( <sub>/2; k) критические точки.

Если</sub> ²_{лев. кр}< ²_набл< ²_{прав. кр} – нет оснований отвергать гипотезу.

Если ²_набл> ²_{прав. кр} или ²_{лев. кр}> ²_набл – нулевую гипотезу отвергают.
Правило 3: При конкурирующей гипотизе H₁: Ϭ²<Ϭ₀² находят критическую точку ²_кр(1-_{α; k). Если} ²_набл> ² _кр.(1-_{α; k)}- нет оснований отвергать нулевую гипотезу. Если ²_набл< ² _кр.(1-_{α; k)}-нулевую гипотезу отвергают.
Практическая часть.