Лекция Законы распределения случайных величин. Лекция Законы распределения. Лекция4. Законы распределения случайных величин. Вопросы Равномерное распределения св

• Название: Лекция4. Законы распределения случайных величин. Вопросы Равномерное распределения св
• Анкор: Лекция Законы распределения случайных величин
• Дата: 08.02.2022
• Размер: 212.5 Kb.
• Имя файла: Лекция Законы распределения.doc
• Тип: Лекция; #354654

Лекция№4. Законы распределения случайных величин.

Вопросы:

1. 
   Равномерное распределения СВ.
   

2. Биноминальный закон распределения.

3. Распределение Пуассона

4. Показательное распределение.

5. Нормальное распределение (распределение Гаусса).

Существует несколько основных типов распределения СВ, которые часто используются на практике. Рассмотрим их.

1. Равномерное распределения СВ.

Определение1. Равномерным называется распределение СВ , значения которых лежат на некотором отрезке [a,b] и имеют постоянную плотность вероятности h .

И 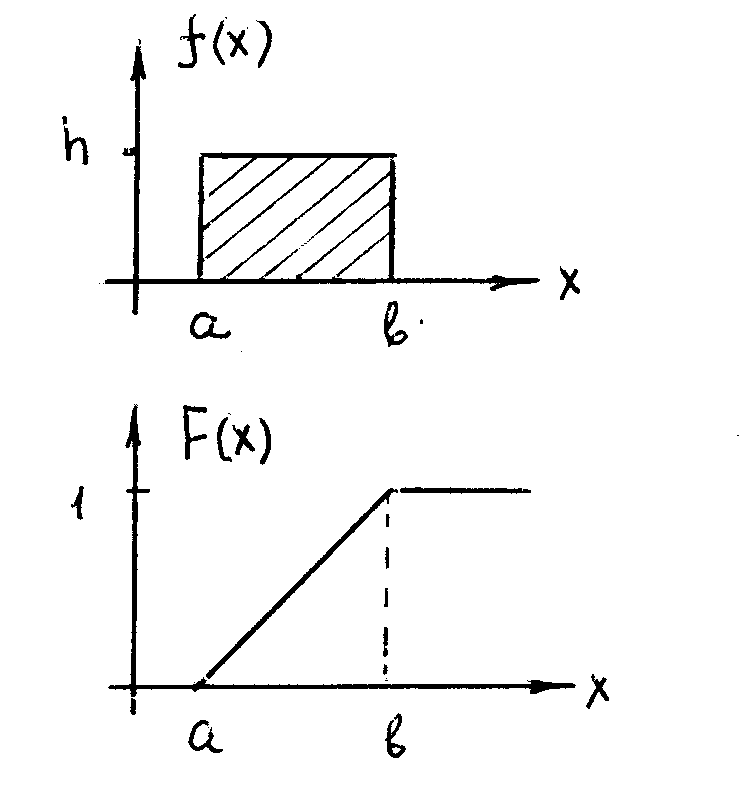з условия нормировки: h(b – a) = 1 h = 1/ (b – a),

f(x) = ;

F(x) = (1)

МО M(Х) = x f(x) dx = = ,

т.е. в центре распределения.

Дисперсия : D(X) = = - =

Среднее квадратичное отклонение = (b – a) / 2

В случае дискретных СВ Х = (х₁, х₂, . . . , х_n) вероятности p_i = 1/n

M(X) = , D(X) = - ( )²
Пример 1. Все показания прибора между двумя соседними целочисленными значениями равновероятны. Они образуют непрерывные СВ на промежутке (0, 1). Найти характеристики такого распределения.

Решение. Имеем равномерное распределение.

f(x) = ;

F(x) =

M(X) =

D(X) = ;

=

2. Биноминальный закон распределения.

Пусть вероятность события А равна p и (1-p)  q. При n повторных испытаниях А может произойти 0, 1, 2, . . . , n раз. Это случайные величины. Вероятность их появления определяет формула Бернулли

P_n(m) = C_n^m p^m q^{n – m} ( 2 )

Определение 2. Сочетание целочисленных СВ и вероятностей ( 2 ) наз. биноминальным законом распределения.

Вычислим M(X). Пусть X_i – число появлений события А при i – ом испытании. Это СВ со следующим распределением

Xi	0	1
pi	q	p

M(X_i) = 0 ^. q + 1 ^. p = p, но X = X₁ + . . .+ X_n и

M(X) = = np.

Найдем D(X) и .

Распределения и математические ожидания для X²i и X_i совпадают.

M(X²_i) = 0²q + 1²p = p. Поэтому D(X_i ) = M(X²_i) - M²(X_i ) = p – p² = p(1 – p) = pq и D(X) = = n p q.

Отсюда = .

3. Распределение Пуассона

Имеем серию n независимых испытаний ( n = 1, 2, 3, . . . ). Считаем, что вероятность появления события А зависит от номера серии P(A) = p_n > 0 и убывает с ростом n так, что для каждой серии среднее число появления события А постоянно, т.е. np_n = ., или p_n = /n . Такая ситуация часто бывает на практике, когда рост n означает увеличение интервала (1, n), а вероятность p_n , по условию задачи, обратно пропорциональна его величине.
Если n достаточно велико, то получаем приближенную формулу Пуассона

P_n(m) = e^{- } , где np_n = . ( 3 )

Определение 3. СВ Х распределена по закону Пуассона , если ее задает таблица

X	0	1	2	3	. . .
P	e- 	e- 	e- 	e- 	. . .

Проверим нормировку P и найдем математическое ожидание

= = = = 1

M(X) = = e^{- } = e^{- } e^ = 

Аналогично получаем M(X²) = ² +  и D(X) = M(X²) - M²(X) = 

=

4. Показательное распределение.

Пусть изменение плотности вероятности f(x) в окрестности точки х пропорционально значению f(x) в этой точке и величине изменения х: f(x) =- f(x)x или d f(x) = -  f(x) dx. Решение этого диф. уравнения df(x) / f(x) = - dx имеет вид ln f(x) = -  x + C или f(x) = C . Проведем нормировку функции при условии x  0 : f(x) dx = C = C/ = 1  C = 

В результате получаем показательное распределение

f(x) = , F(x) =

M(X) = 1/ , D(X) = 1/² , = 1/ ( 4)
Если эксперимент дает M(X) = ,то можно считать, что распределение показательное.

Если при показательном распределении неизвестно , то его определяют по математическому ожиданию:  = 1/M(X) .
Показательный закон надежности. Пусть Т – время безотказной работы какого-либо устройства. Значения переменной величины 0 < T < t задают непрерывное множество СВ, которые определяют факт отключения устройства в момент времени Т. Тогда, функция распределения вероятностей этих СВ F(t) = P(T < t) определяет вероятность отключения устройства к моменту времени t . Вероятность противоположного события, т.е. безотказной работы за время t, равна R(t) = 1 – F(t) и наз. функцией надежности.

В случае показательного распределения F(t) = 1 – e^-t получаем показательный закон надежности R(t) = e^-t , где  наз. интенсивность отказа. Это случай, когда безотказная работа устройства зависит только от величины временного интервала и количества устройств, действующих к моменту времени t .




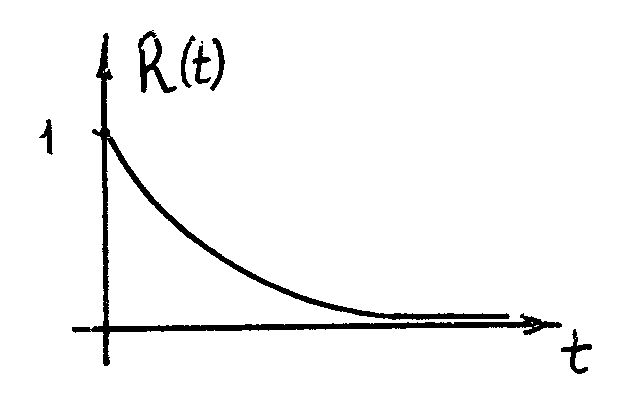
Пример 2. Время безотказной работы радиолампы определяется функцией надежности R(t) = (1/300) e^-t/300 . Найти а) среднее значение времени работы; б) вероятность отказа за промежуток от 150 до 450 часов; в) вероятность работы не менее 600 часов. Решение.

а) Среднее время работы равно математическому ожиданию M(t) = 1/ = 300 часов;

б) P(150 < t < 450) = F(450) – F(150) = e^-150/300 - e^-450/300 = = 0.38;

в) Это значение функции надежности R(600) = e^-600/300 = 1/e² = 0.1352 .
5. Нормальное распределение (распределение Гаусса).

В правую часть диф. уравнения для показательного распределения введем дополнительный множитель (х – m) : df(x) / f(x) = -(x – m) dx . Это означает, что величина изменения плотности вероятности в окрестности точки х будет линейно зависеть и от смещения этой точки относительно некоторой точки m. Решение дифференциального. уравнения – f(x) = C наз. кривой Гаусса.

Это симметричная, быстро затухающая функция. Имеет куполообразную форму с вершиной при x = m и приводит к нормальному закону распределению СВ




( ( 5 )

где а– определяет точку максимума и ось симметрии,

 - расстояние от этой оси до точки перегиба или M(X) = а, D(X) = .

Особенности нормального распределения

а) Наиболее вероятны значения x, близкие к ожидаемому среднему значению а.

б) Отклонения от среднего значения а в обе стороны равновероятны.

в) Большие отклонения x от среднего значения а маловероятны.

Площадь под кривой Гаусса всегда равна единице, что соответствует полной вероятности. Поэтому при уменьшении  увеличивается вероятность значений, близких к а, рассеяние уменьшается, кривая Гаусса сжимается. При увеличении  график кривой Гаусса становится более расплывчатым, что говорит об увеличении рассеяния.
Это распределение играет фундаментальную роль в теории ошибок измерений. Согласно центральной предельной теореме закон распределения суммы большого числа независимых СВ, влияние каждого из которых на всю сумму ничтожно мало, близок к нормальному. Доказана А.М.Ляпуновым (1857 – 1918) .

Вероятности нормального распределения N(x; m,  ) :

P(a< X < b) = F(b) - F(a) = f(x)dx = dx ( 6 )

В случае m = 0,  = 1 функция ( 6 ) наз. плотностью нормированного и центрированного распределения (локальная функция Лапласа) ( 7 )

а соответствующая функция распределения (х) = ( 8)
наз. функцией Лапласа или интегралом вероятностей.

(x) - нечетная функция и вычисляется с помощью таблиц. После простой замены переменных в ( 6 ) имеем

P(a<X<b) = [ -  ] ( 9 )

Вероятность отклонения Х от m на величину меньшую  по симметричному участку относительно m равна

P(|X – m| < ) = P(m -  < X < m + ) =  -  = 2 ( 10 )
Пример 3. Определить среднее квадратичное отклонение  случайных ошибок прибора, если они подчиняются нормальному закону. Систематических ошибок прибор не имеет (m = 0), а случайные с вероятностью 0,8 не выходят за пределы 20 (м).
Решение. По условию задачи Р( |x| 20 ) = 0,8 или по формуле ( 10)

 -  = 2 = 0,8. По таблице находим 20/ = 1,29 или  = 15,5 (м)
Пример 4. СВ Х распределена по нормальному закону с математиче6ским ожиданием m = 40 и дисперсией D = 160. Вычислить вероятность попадания СВ в интервал (30, 80)
Решение. В формуле ( 9 ) a = 30, b = 80, m = 40,  =
P(30 -  = (1) + (0,25) = 0,34 + 0,1 = 0,35

Пример 5. Правило «трех сигм».

Вероятность того, что абсолютная величина отклонения «X–а» меньше , составляет (10):



В частности, если =3, получим:



Этот результат называют правилом «трех сигм»: почти достоверно (на 99,7%), что значения нормально распределенной случайной величины отличаются от своего среднего значения а менее, чем на 3, то есть практически все значения нормально распределенной случайной величины Х попадают в интервал: (а - 3; а+3), см. рис. 1.



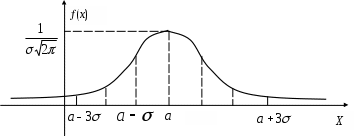
Рис.1