Курс_лекций_информатика_10-11. Курс лекций Инф 1 курс. Пояснительная записка Курс лекций учебной дисциплины Информатика
 Скачать 3.88 Mb. Скачать 3.88 Mb.
|
|
Тема 2.2. Подходы к понятию информации и измерению информации. Информационные объекты различных видов ПЛАН Форматы представления чисел в компьютере Представление целого положительного числа в компьютере Представление целого отрицательного числа в компьютере Представление вещественного (действительного) числа в компьютере Форматы представления чисел в компьютере Для хранения чисел в памяти компьютера используется два формата: целочисленный (естественная форма) и с плавающей точкой (нормализованная форма) (точка — разделительный знак для целой и дробной части числа). Целочисленный формат (формат с фиксированной точкой) используется для представления в компьютере целых (англ. integer) положительных и отрицательных чисел. Для этого, как правило, используются форматы, кратные байту: 1, 2, 4 байта. В форме с фиксированной запятой числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой (или точки), отделяющей целую часть от дробной. Эта форма проста и привычна для большинства пользователей, но имеет небольшой диапазон представления чисел и поэтому не всегда пригодна при вычислениях. Если же в результате какой-либо арифметической операции получается число, выходящее за допустимый диапазон, то происходит переполнение разрядной сетки, и все дальнейшие вычисления теряют смысл. Однобайтовое представление применяется только для положительных целых чисел. В этом формате отсутствует знаковый разряд. Наибольшее двоичное число, которое может быть записано при помощи 1 байта, равно 11111111, что в десятичной системе счисления соответствует числу 25510. Для положительных и отрицательных целых чисел обычно используется 2 и 4 байта, при этом старший бит выделяется под знак числа: 0 - плюс, 1 - минус. Самое большое (по модулю) целое число со знаком, которое может поместиться в 2-байтовом формате, это число 0111111111111111, то есть при помощи подобного кодирования можно представить числа от −32 76810 до 32 76710. Если число вышло за указанные границы, произойдет переполнение! Поэтому при работе с большими целыми числами под них выделяется больше места, например 4 байта. Формат с плавающей точкой (нормализованная форма) используется для представления в компьютере действительных чисел (англ. real). Числа с плавающей точкой размещаются, как правило, в 4 или 8 байтах. Нормализованная форма представления чисел обеспечивает огромный диапазон их записи и является основной в современных ЭВМ. Представление целого положительного числа в компьютере Для представления целого положительного числа в компьютере используется следующее правило: число переводится в двоичную систему; результат дополняется нулями слева в пределах выбранного формата; последний разряд слева является знаковым, в положительном числе он равен 0. Например, положительное число +13510 в зависимости от формата представления в компьютере будет иметь следующий вид: - для формата в виде 1 байта - 10000111 (отсутствует знаковый разряд); - для формата в виде 2 байтов - 0000000010000111; - для формата в виде 4 байтов - 00000000000000000000000010000111. 3.Представление целого отрицательного числа в компьютере Для представления целого отрицательного числа в компьютере используется дополнительный код. Такое представление позволяет заменить операцию вычитания числа операцией сложения с дополнительным кодом этого числа. Знаковый разряд целых отрицательных чисел всегда равен 1. Для представления целого отрицательного числа в компьютере используется следующее правило: - число без знака переводится в двоичную систему; - результат дополняется нулями слева в пределах выбранного формата; - полученное число переводится в обратный код (нули заменяются единицами, а единицы - нулями); - к полученному коду прибавляется 1. Обратный код для положительного двоичного числа совпадает с его прямым кодом, а для отрицательного числа нужно во всех разрядах, кроме знакового, нули заменить единицами и наоборот. Дополнительный код для положительного числа совпадает с его прямым кодом, а для отрицательного числа образуется путем прибавления 1 к обратному коду. Отрицательное число может быть представлено в виде 2 или 4 байт. Например, представим число −13510 в 2-байтовом формате: - 13510→ 10000111 (перевод десятичного числа без знака в двоичный код); - 0000000010000111(дополнение двоичного числа нулями слева в пределах формата); - 0000000010000111→ 1111111101111000(перевод в обратный код - инвертирование); - 1111111101111000→ 1111111101111001 (перевод в дополнительный код (+1)).     4. Особенности целочисленной машинной арифметики Числовые расчеты могут производиться на множестве целых чисел или на множестве вещественных чисел. С математической точки зрения целые числа являются подмножеством множества вещественных чисел. Поэтому, казалось бы, можно было бы и не разделять числа на целые и вещественные и иметь дело только с вещественным числовым типом данных. Однако целочисленная арифметика на ЭВМ имеет три очень существенных преимущества по сравнению с вещественной арифметикой: • целые числа всегда представимы своими точными значениями; • операции целочисленной арифметики дают точные результаты; • операции целочисленной арифметики выполняются быстрее, чем операции вещественной («плавающей») арифметики. Недостатком целого типа данных является сравнительно узкий диапазон допустимых значений (для типа Integer — от -32768 до 32767). При исполнении программы автоматически не контролируется выход значения целой величины за эти границы. В этом случае получается ошибочный результат. Если такая опасность существует, то программист должен сам предусматривать в своей программе предупреждение целочисленного переполнения. Чаще всего целый тип используется для представления счетчиков, номеров, индексов и других целочисленных величин. 5.Представление вещественного (действительного) числа в компьютере Вещественное число может быть представлено в экспоненциальном виде, например: 1600000010=0,16⋅108 −0,000015610=−0,156⋅10−4 В этом формате вещественное число (R) представляется в виде произведения мантиссы (m) и основания системы счисления (P) в целой степени (n), называемой порядком. Представим это в общем виде, как: R=m⋅Pn. Порядок n указывает, на какое количество позиций и в каком направлении должна сместиться в мантиссе точка (запятая), отделяющая дробную часть от целой. Мантисса, как правило, нормализуется, то есть представляется в виде правильной дроби 0 < m < 1. Мантисса должна быть правильной дробью, у которой первая цифра после точки (запятой в обычной записи) отлична от нуля. Если это требование выполнено, то число называется нормализованным. При представлении в компьютере действительного числа с плавающей точкой тоже используется нормализованная мантисса и целый порядок. И мантисса и порядок представляются в двоичном виде, как это было описано выше. Для размещения вещественного числа обычно используется 2 или 4 байта. В 2-байтовом формате представления вещественного числа первый байт и три разряда второго байта выделяются для размещения мантиссы, в остальных разрядах второго байта размещаются порядок числа, знаки числа и порядка.  В 4-байтовом формате представления вещественного числа первые три байта выделяются для размещения мантиссы, в четвертом байте размещаются порядок числа, знаки числа и порядка. 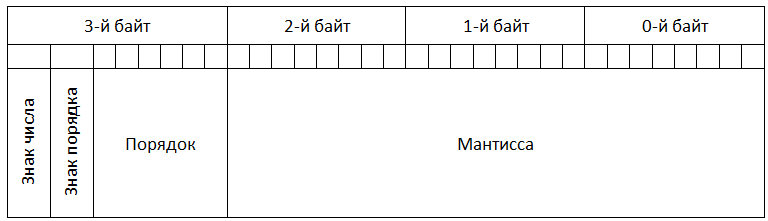 Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Пример записи числа 6,2510=110,012=0,11001⋅211, представленного в нормализованном виде, в четырёхбайтовом формате с семью разрядами для записи порядка. 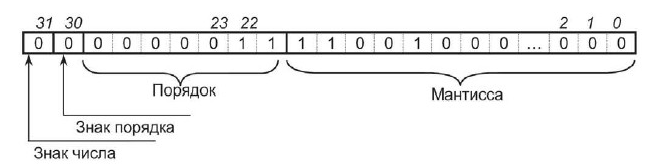 Тема 2.3. Принципы обработки информации компьютером ПЛАН: 1. Принципы обработки информации компьютером 2. Арифметические и логические основы работы компьютера 3. Вопросы самоконтроля 1. Принципы обработки информации компьютером Компьютер или ЭВМ (электронно-вычислительная машина) – это универсальное техническое средство для автоматической обработки информации. Аппаратное обеспечение (Hardwear) компьютера – это все устройства, входящие в его состав и обеспечивающие его исправную работу. Несмотря на разнообразие компьютеров в современном мире, все они строятся по единой принципиальной схеме, основанной на фундаменте идеи программного управления Чарльза Бэббиджа (середина XIX в). Эта идея была реализована при создании первой ЭВМ ENIAC в 1946 году коллективом учёных и инженеров под руководством известного американского математика Джона фон Неймана, сформулировавшего концепцию ЭВМ с вводимыми в память программами и числами -программный принцип. Главные элементы концепции: двоичное кодирование информации; программное управление; принцип хранимой программы; принцип параллельной организации вычислений, согласно которому операции над числом проводятся по всем его разрядам одновременно. С тех пор структуру (архитектуру) современных компьютеров часто называют неймановской. ОБЩАЯ СХЕМА КОМПЬЮТЕРА Персональный компьютер (ПК) в своём минимально необходимом составе согласно этой схеме включает: основные устройства ввода: клавиатуру и манипулятор «мышь»; основное устройство вывода: монитор; центральная часть располагается в системном блоке; внешняя память располагается на носителях – дисках и приводится в действие специальными приводами – дисководами; в единую конфигурацию все части ПК соединены с помощью устройств сопряжения. В основе строения ПК лежат два важных принципа: магистрально-модульный принцип и принцип открытой архитектуры. Согласно первому все части и устройства изготавливаются в виде отдельных блоков, информация между которыми передаётся по комплекту соединений, объединённых в магистраль. При этом общую схему ПК можно представить в следующем виде: 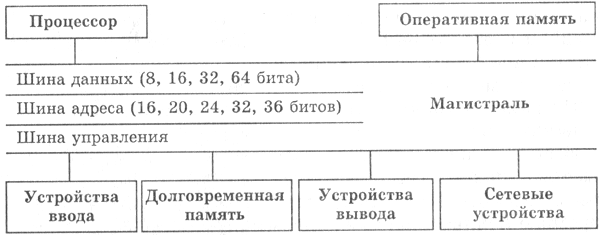 Второй принцип построения ПК – открытая архитектура – предполагает возможность сборки компьютера из независимо изготовленных частей, доступную всем желающим (подобно детскому конструктору). 2. Арифметические и логические основы работы компьютера Логика, как наука развивается с IV в. до н. э. начиная с трудов Аристотеля. Именно он подверг анализу человеческое мышление, такие его формы, как понятие, суждение, умозаключение. Логика – (от греч. “логос”, означающего “слово” и “смысл”) – наука о законах, формах и операциях правильного мышления. Ее основная задача заключается в нахождении и систематизации правильных способов рассуждения. 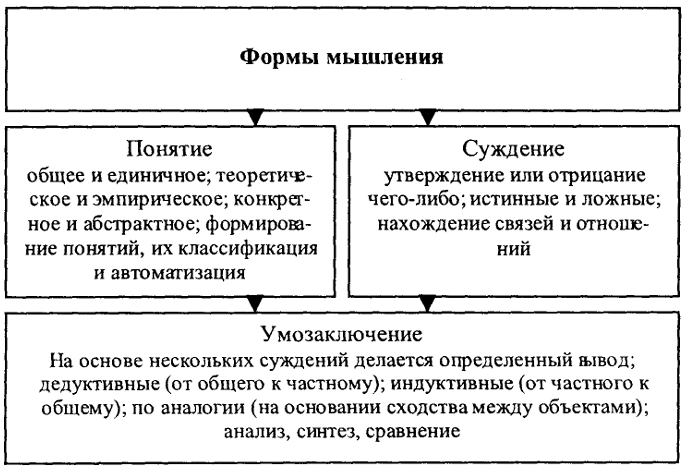 Рис. 1. Основные формы абстрактного мышления Понятие – это форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов. Всякое понятие имеет содержание и объем. Например, понятие “Черное море” – отражает единичный предмет, “Сиамская кошка” – отражает класс сиамских кошек. Высказывание (суждение) – некоторое предложение, которое может быть истинно (верно) или ложно. Например, Абакан – столица Хакасии. Утверждение – суждение, которое требуется доказать или опровергнуть. Рассуждение – цепочка высказываний или утверждений, определенным образом связанных друг с другом. Умозаключение – логическая операция, в результате которой из одного или нескольких данных суждений получается (выводится) новое суждение. Умозаключения бывают: Дедуктивные (от общего к частному) – Все ученики ходят в школу. Вася – ученик. Вася ходит в школу. Индуктивные (от частного к общему) – Банан и персик – сладкие. Значит, все фрукты сладкие на вкус. Аналогия – Наши коровы едят траву и дают молоко. В Австралии есть поля, коровы едят эту траву. Следовательно, австралийские коровы тоже дают молоко. В алгебре логики высказывания обозначаются именами логических переменных (А, В, С). Истина, ложь – логические константы. Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных логическое выражение может принимать одно из двух возможных значений: ИСТИНА (логическая 1) или ЛОЖЬ (логический 0). Сложное логическое выражение – логическое выражение, составленное из одного или нескольких простых (или сложных) логических выражений, связанных с помощью логических операций. Логические операции и таблицы истинности 1) Логическое умножение или конъюнкция: Конъюнкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно. Обозначение: F = A & B. Таблица истинности для конъюнкции
2) Логическое сложение или дизъюнкция: Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны. Обозначение: F = A + B. Таблица истинности для дизъюнкции
3) Логическое отрицание или инверсия: Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО. Таблица истинности для инверсии
4) Логическое следование или импликация: Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием. Таблица истинности для импликации
5) Логическая равнозначность или эквивалентность: Эквивалентность - это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность. Таблица истинности для эквивалентности
Порядок выполнения логических операций в сложном логическом выражении 1. Инверсия; 2. Конъюнкция; 3. Дизъюнкция; 4. Импликация; 5. Эквивалентность. Для изменения указанного порядка выполнения логических операций используются скобки. Вопросы самоконтроля 1. Объясните состав ПК? 2. Что такое Инверсия? 3. Что такое Что такое Импликация? 4. Что такое Дизъюнкция? 5. Опишите основные формы мышления |
