2. Информационные объекты различных видов.
Информация - это ключевое понятие современной науки, которое стоит в одном ряду с такими как "вещество" и "энергия". Существует три основные интерпретации понятия "информация".
Научная интерпретация. Информация - исходная общенаучная категория, отражающая структуру материи и способы ее познания, несводимая к другим, более простым понятиям.
Абстрактная интерпретация. Информация - некоторая последовательность символов, которые несут как вместе, так в отдельности некоторую смысловую нагрузку для исполнителя.
Конкретная интерпретация. В данной плоскости рассматриваются конкретные исполнители с учетом специфики их систем команд и семантики языка. Так, например, для машины информация - нули и единицы; для человека - звуки, образы, и т.п.
Существуют несколько концепций (теорий) информации.
Первая концепция (концепция К. Шеннона), отражая количественно-информационный подход, определяет информацию как меру неопределенности (энтропию) события. Количество информации в том или ином случае зависит от вероятности его получения: чем более вероятным является сообщение, тем меньше информации содержится в нем.
Вторая концепция рассматривает информацию как свойство (атрибут) материи. Ее появление связано с развитием кибернетики и основано на утверждении, что информацию содержат любые сообщения, воспринимаемые человеком или приборами. Наиболее ярко и образно эта концепция информации выражена академиком В.М. Глушковым.
Третья концепция основана на логико-семантическом (семантика - изучение текста с точки зрения смысла) подходе, при котором информация трактуется как знание, причем не любое знание, а та его часть, которая используется для ориентировки, для активного действия, для управления и самоуправления. Иными словами, информация - это действующая, полезная, "работающая" часть знаний. Представитель этой концепции В.Г. Афанасьев.
В настоящее время термин информация имеет глубокий и многогранный смысл. Во многом, оставаясь интуитивным, он получает разные смысловые наполнения в разных отраслях человеческой деятельности:
в житейском аспекте под информацией понимают сведения об окружающем мире и протекающих в нем процессах, воспринимаемые человеком или специальными устройствами;
в технике под информацией понимают сообщения, передаваемые в форме знаков или сигналов;
в теории информации (по К.Шеннону) важны не любые сведения, а лишь те, которые снимают полностью или уменьшают существующую неопределенность;
в кибернетике, по определению Н. Винера, информация - эта та часть знаний, которая используется для ориентирования, активного действия, управления, т.е. в целях сохранения, совершенствования, развития системы;
в семантической теории (смысл сообщения) - это сведения, обладающие новизной, и так далее...
Такое разнообразие подходов не случайность, а следствие того, что выявилась необходимость осознанной организации процессов движения и обработки того, что имеет общее название - информация.
По способу восприятия информацию разделяют на следующие виды: визуальная, аудиальная, вкусовая, обонятельная и тактильная.
Человек создает приборы, позволяющие получать информацию, которая недоступна ему в непосредственных ощущениях. Микроскопы, телескопы, термометры, спидометры - перечень, который можно продолжать и продолжать. Аналогам органов чувств человека в технических приборах соответствуют различные датчики. Получение информации называется вводом. В персональном компьютере за ввод информации отвечают специальные устройства ввода: клавиатура, сканер, дигитайзер, микрофон, мышь и многое другое.
Человек воспринимает информацию с помощью органов чувств. Воспринимаемая информация поступает в виде энергетических сигналов (свет, звук, тепло) и излучений (вкус и запах), причем процесс поступления этих сигналов происходит непрерывно.
Информация необходима человеку не вообще, а конкретно в нужное время для ориентирования в окружающем мире и принятия решений о дальнейших действиях. При качественной оценке получаемой информации говорят о следующих ее свойствах:
Свойства информации:
Информация достоверна, если она отражает истинное положение дел. Недостоверная информация может привести к неправильному пониманию или принятию неправильных решений. Достоверная информация со временем может стать недостоверной, так как она обладает свойством устаревать, то есть перестаёт отражать истинное положение дел.
Информация полна, если её достаточно для понимания и принятия решений. Как неполная, так и избыточная информация сдерживает принятие решений или может повлечь ошибки.
Точность информации определяется степенью ее близости к реальному состоянию объекта, процесса, явления и т.п.
Ценность информации зависит от того, насколько она важна для решения задачи, а также от того, насколько в дальнейшем она найдёт применение в каких-либо видах деятельности человека.
Только своевременно полученная информация может принести ожидаемую пользу. Одинаково нежелательны как преждевременная подача информации (когда она ещё не может быть усвоена), так и её задержка. Если ценная и своевременная информация выражена непонятным образом, она может стать бесполезной.
Информация становится понятной, если она выражена языком, на котором говорят те, кому предназначена эта информация.
Информация должна преподноситься в доступной (по уровню восприятия) форме. Поэтому одни и те же вопросы по-разному излагаются в школьных учебниках и научных изданиях.
3. Универсальность дискретного (цифрового) представления информации
Давайте подумаем об информации как о сигнале. Мы знаем, что сигнал рассматривается с позиции носителя информации по техническим средствам передачи.
Для передачи информации, или, правильнее сказать, данных, используется физический процесс, который может быть описан математической формулой и называется сигналом. Именно сигналы различают по способу их представления как аналоговые и дискретные (см. рис. 1 и 2).
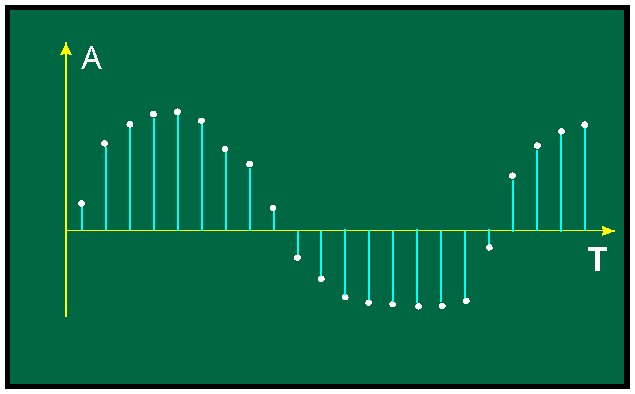 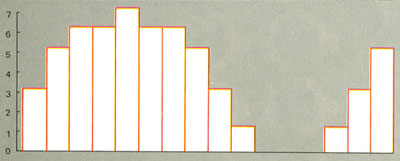
Рис. 1. Аналоговый сигнал Рис. 2. Дискретный сигнал
Аналоговая информация характеризуется плавным изменением ее параметров. Основные параметры наиболее простых синусоидальных аналоговых сигналов могут непрерывно и плавно меняться.
Дискретная информация базируется на ряде фиксированных уровней представления заданных параметров, взятых в определенные промежутки времени. Если этих уровней много, можно говорить о цифровом представлении информации, то есть когда в определенные дискретные моменты они принимают конкретные дискретные значения. К счастью, аналоговую информацию легко преобразовать в цифровую. Это делают так называемые аналогоцифровые преобразователи (АЦП). Обратное преобразование обеспечивают цифроаналоговые преобразователи (ЦАП).
В качестве носителей аналоговой информации могут использоваться различные физические величины, принимающие различные значения на некотором интервале, например, электрический ток, радиоволна и т.д. При дискретизации, то есть при преобразовании непрерывных изображений и звука в набор дискретных значений в форме кодов, за основу берется какое-либо конкретное значение, а любые другие, отличающиеся от нормы, просто игнорируются.
Аналоговыми устройствами являются:
телевизор - луч кинескопа непрерывно перемещается по экрану, чем сильнее луч, тем ярче светится точка, в которую он попадает; изменение свечения точек происходит плавно и непрерывно;
проигрыватель грампластинок – чем больше высота неровностей на звуковой дорожке, тем громче звучит звук;
телефон – чем громче мы говорим в трубку, тем выше сила тока, проходящего по проводам, тем громче звук, который слышит собеседник.
К дискретным устройствам относятся:
монитор – яркость луча изменяется не плавно, а скачкообразно (дискретно). Луч либо есть, либо его нет. Если луч есть, то мы видим яркую точку (белую или цветную). Если луча нет, мы видим черную точку. Поэтому изображение на экране монитора получается более четким, чем на экране телевизора;
проигрыватель аудиокомпакт-дисков – звуковая дорожка представлена участками с разной отражающей способностью;
струйный принтер – изображение состоит из отдельных точек разного цвета.
Человек благодаря своим органам чувств привык иметь дело с аналоговой информацией, а в компьютере информация представлена в цифровом виде. Преобразование графической и звуковой информации из аналоговой формы в дискретную производится путем дискретизации, то есть разбиения непрерывного графического изображения или звукового сигнала на отдельные элементы.
Чувствительные органы живого организма в основном по своей природе дискретны. Зрительные образы воспринимают клетки сетчатки глаза, тактильные ощущения возникают в чувствительных нейронах, запахи воспринимаются рецепторами обоняния, каждый из которых в любой момент времени находится либо в возбужденном, либо невозбужденном состоянии. Все чувственные восприятия преобразуются в организме из дискретной формы в непрерывную, причем информация хранится не в отдельных нейронах головного мозга, а распределена по нему целиком. Непрерывность представления, например, зрительной информации позволяет человеку уверенно воспринимать динамику окружающего мира. Дискретные величины принимают не все возможные, а только определенные значения, и их можно пересчитать.
В технике непрерывная информация называется аналоговой. Многие устройства, созданные человеком, работают с аналоговой информацией. Луч кинескопа телевизора перемещается по экрану, вызывая свечение точек. Чем сильнее луч, тем ярче свечение. Изменение свечения происходит плавно и непрерывно. Проигрыватель грампластинок, ртутный термометр, манометр - примеры аналоговых устройств. Некоторые бытовые приборы могут иметь как аналоговую, так и цифровую конструкцию. К примеру, тонометр - прибор для измерения кровяного давления. Существенным отличием является то, что аналоговый прибор может выдать абсолютно произвольную величину показаний (чуть больше или меньше деления), а набор показаний у цифрового прибора ограничен количеством цифр на индикаторе. Компьютер работает исключительно с дискретной (цифровой) информацией. Память компьютера состоит из отдельных битов, а значит, дискретна. Датчики, посредством которых воспринимается информация, измеряют в основном непрерывные характеристики - температуру, нагрузку, напряжение и т.д. Встает проблема преобразования аналоговой информации в дискретную форму.
Идея дискретизации непрерывного сигнала заключается в следующем. Пусть имеется некоторый непрерывный сигнал. Можно допустить, что на маленьких промежутках времени значение характеристик этого сигнала постоянно и меняется мгновенно в конце каждого промежутка. "Нарезав" весь временной интервал на эти маленькие кусочки и взяв на каждом из них значение характеристик, получим сигнал с конечным числом значений. Таким образом, он станет дискретным. Непрерывная величина часто ассоциируется с графиком функции, а дискретная - с таблицей ее значений.
Такой процесс называется оцифровкой аналогового сигнала, а преобразование информации - аналого-цифровым преобразованием. Точность преобразования зависит от величины дискретности - частоты дискретизации: чем выше частота дискретизации, тем ближе цифровая информация к качеству аналоговой. Но и тем больше вычислений приходится делать компьютеру и тем больше информации хранить и обрабатывать.
Дискретизация – это преобразование непрерывных изображений и звука в набор дискретных значений в форме кодов.
При передаче дискретных данных по каналам связи применяются два основных типа физического кодирования – на основе синусоидального несущего сигнала и на основе последовательности прямоугольных импульсов. Первый способ часто называется также модуляцией или аналоговой модуляцией, подчеркивая тот факт, что кодирование осуществляется за счет изменения параметров аналогового сигнала. Второй способ обычно называют цифровым кодированием. Эти способы отличаются шириной спектра результатирующего сигнала и сложностью аппаратуры, необходимой для их реализации.
В настоящее время все чаще данные, изначально имеющие аналоговую форму (речь, телевизионное изображение), передаются по каналам связи в дискретном виде, то есть в виде последовательности единиц и нулей. Процесс представления аналоговой информации в дискретной форме называется дискретной модуляцией. Аналоговая модуляция применяется для передачи дискретных данных по каналам с узкой полосой частот, типичным представителем которых является канал тональной частоты (телефонная сеть).
В простых вычислительных машинах, в таких, как цифровые электромеханические или аналоговые, перенастройка на различные задачи осуществлялась с помощью изменения системы связей между элементами на специальной коммутационной панели. В современных универсальных компьютерах такие изменения производятся с помощью запоминания в специальном устройстве, накапливающем информацию, той или иной программы ее работы.
В отличие от аналоговых машин, оперирующих непрерывной информацией, современные компьютеры имеют дело с дискретной информацией, на входе и выходе которых в качестве такой информации могут выступать любые последовательности десятичных цифр, букв, знаков препинания и других символов. Внутри системы эта информация кодируется в виде последовательности сигналов, принимающих лишь два различных значения.
В то время как возможности аналоговых машин ограничены преобразованиями строго ограниченных типов сигналов, современные компьютеры обладают свойством универсальности, иными словами, компьютер может производить преобразования любых буквенно-цифровых данных благодаря программе, составленной для выполнения той или иной задачи. Эта способность компьютера достигается за счет универсальности его системы команд, то есть элементарных преобразований информации.
Свойство универсальности компьютера не ограничивается возможностью оперирования одной лишь буквенно-цифровой информацией. В данном виде может быть представлена (закодирована) любая дискретная информация, а также – с любой заданной степенью точности – произвольная непрерывная информация. Таким образом, компьютеры могут рассматриваться как универсальные преобразователи информации. Свойство универсальности современных компьютеров открывает возможность моделирования с их помощью любых других преобразователей информации, в том числе любых мыслительных процессов.
Технологии цифровой обработки акустических сигналов и изображений находят все более широкое применение в различных областях, в частности при идентификации пользователей или для построения многоуровневых систем защиты. Вместе с тем в перечне основных предъявляемым к соответствующим системам требований на первом месте стоит универсальность, быстрота и эффективность выполнения различных процедур обработки на основе использования стандартных недорогих технических средств, входящих в комплект традиционной офисной техники и компьютерной телефонии: ПК, сканера, принтера, звуковой платы, модема. Для реализации таких систем нужны подходы, позволяющие обрабатывать акустический сигнал и речь.
Практически 80% информации человек получает через зрение, что означает доминирование зрительных рецепторов в жизнедеятельности человека. Вся информация в аппарате мышления человека сохраняется в виде образов, причем в этом образе сконцентрирована информация, полученная всеми рецепторами человека. Можно сделать вывод, что информация в памяти человека хранится в виде графических объектов. Развивая гипотезу о том, что любая информация, получаемая человеком извне, проходит стадию преобразования в изображения с последующей их целенаправленной обработкой, можно вывести последовательность процедур, пригодную для реализации в автоматизированных системах обработки данных различного рода, в том числе и в речи:
предобработка, когда независимо от вида полученной информации осуществляется ее преобразование к общему виду первичных описаний в виде двухмерных матриц данных, имеющих неотрицательные значения, которые можно рассматривать как изображения, образы;
обработка предполагает, что на основе каких-либо общих принципов, методов и алгоритмов осуществляются преобразования полученных первичных данных для достижения поставленных целей (сжатие, «шумоочистка», сравнение, распознавание и др.);
получение новых знаний и принятие решений основываются на заключении из характера и вида полученной из внешнего мира информации, а также результатов ее обработки для выполнения конкретных действий в соответствии с общей стратегией поведения человека.
Практическая значимость этой гипотезы состоит в том, что интеллектуальные возможности человека по анализу и обработке визуальной информации, а также наработанный научный потенциал в области восстановления, распознавания и обработки изображений можно распространить сегодня на существующие технологии обработки информации иного рода, в том числе на акустические сигналы и речь.
Люди воспринимают пространство как «глубину», и изображения, формируемые мысленным взором, представляются им трехмерными. Однако в точных дисциплинах редко применяется обработка трехмерных изображений, что объясняется очевидными техническими трудностями работы с ними, а также недостаточным пониманием природы процесса восприятия изображений. В большинстве практических приложений исследователи имеют дело с квазитрехмерными изображениями, когда по двум известным параметрам, например, частоте и времени, строится некая двухмерная матрица, значения которой определяются значениями третьего известного параметра, например, мощностью и амплитудой рассчитанного мгновенного спектра.
4. Представление информации в различных системах счисления
Позиционные и непозиционные системы счисления.
Понятие числа является фундаментальным как для математики, так и для информатики. С числами связано еще одно важное понятие — система счисления.
Система счисления — это способ изображения чисел и соответствующие ему правила действий над числами.
Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить нанепозиционные и позиционные.
В древние времена, когда люди начали считать, появилась потребность в записи чисел. Первоначально количество предметов отображали равным количеством каких-нибудь значков: насечек, черточек, точек.
Изучение археологами «записок» времен палеолита на кости, камне, дереве показало, что люди стремились группировать отметки по 3, 5, 7, 10 штук. Такая группировка облегчала счет. Люди учились считать не только единицами, но и тройками, пятерками и пр. Поскольку первым вычислительным инструментом учеловека были пальцы, поэтому и счет чаще всего вели группами по 5 или по 10 предметов.
В дальнейшем свое название получили десяток десятков (сотня), десяток сотен (тысяча) и так далее. Такие узловые числа для удобства записи стали обозначать особыми значками — цифрами. Если при подсчете предметов их оказывалось 2 сотни, 5 десятков и еще 4 предмета, то при записи этой величины дважды повторяли знак сотни, пять раз — знак десятков и четыре раза знак единицы.
В таких системах счисления от положения знака в записи числа не зависит величина, которую он обозначает; поэтому они называются непозиционными системами счисления.
Непозиционными системами пользовались древние египтяне, греки, римляне и некоторые другие народы древности.
На Руси вплоть до XVIII века, использовалась непозиционная система славянских цифр. Буквы кириллицы (славянского алфавита) имели цифровое значение, если над ними ставился специальный знак
титло. Например Ã — 1, 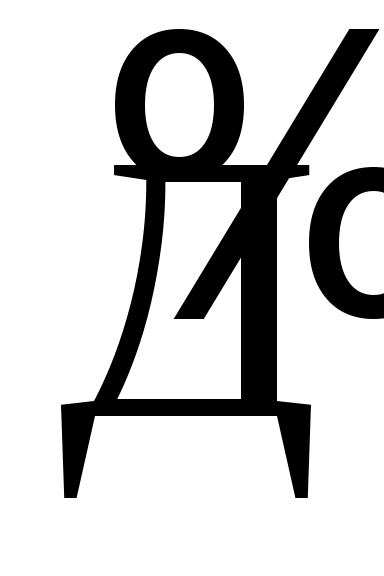 — 4, — 4, 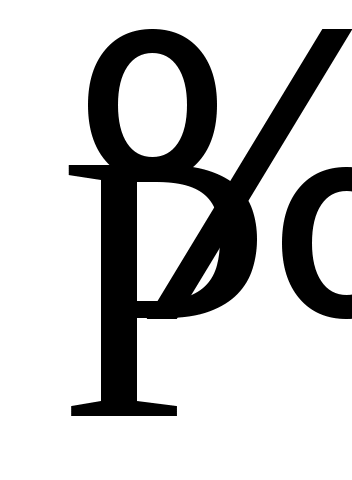 — 100. — 100.
Непозиционные системы счисления были более или менее пригодны для выполнения сложения и вычитания, но совсем не удобны при умножении и делении.
Идея позиционной системы счисления впервые возникла в древнем Вавилоне.
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции.
Количество используемых цифр называется основанием позиционной системы счисления.
Система счисления, применяемая в современной математике, является позиционной десятичной системой. Ее основание равно десяти, так как запись любых чисел производится с помощью десяти цифр:
0,1, 2, 3, 4, 5, 6, 7, 8, 9.
Хотя десятичную систему принято называть арабской, но зародилась она в Индии, в V веке. В Европе об этой системе узнали в XII веке из арабских научных трактатов, которые были переведены на латынь. Этим и объясняется название «арабские цифры». Однако широкое распространение в науке и в обиходе десятичная позиционная система получила только в XVIвеке. Эта система позволяет легко выполнять любые арифметические вычисления, записывать числа любой величины. Распространение арабской системы дало мощный толчок развитию математики.
С позиционной десятичной системой счисления вы знакомы с раннего детства, только, возможно, не знали, что она так называется.
Позиционный тип этой системы легко понять на примере любого многозначного числа. Например, в числе 333 первая тройка означает три сотни, вторая — три десятка, третья — три единицы. Одна и та же цифра в зависимости от позиции в записи числа обозначает разные величины.
333 = 3x100 + 3x10 + 3.
Еще пример:
32478 = 3 х 10000 + 2 х 1000 + 4 х 100 + 7 х 10 + 8 =
= 3 х 104 + 2 х 103 + 4 х 102 + 7 х 101 + 8 х 100.
Отсюда видно, что всякое десятичное число можно представить как сумму произведений составляющих его цифр на соответствующие степени десятки. То же самое относится и к десятичным дробям.
26,387 = 2 х 101 + 6 х 100+ 3 х 10-1 + 8 х 10-2 + 7 х 10-3
Системы счисления, используемые в ЭВМ
Очевидно, число «десять» — не единственно возможное основание позиционной системы. Известный русский математик Н.Н.Лузин так выразился по этому поводу: «Преимущества десятичной системы не математические, а зоологические. Если бы у нас на руках было не десять пальцев, а восемь, то человечество пользовалось бы восьмеричной системой».
За основание позиционной системы счисления можно принять любое натуральное число большее 1. Упомянутая выше вавилонская система имела основание 60. Следы этой системы сохранились до наших дней в порядке счета единиц времени (1 час = 60 мин, 1 мин = 60 с).
Для записи чисел в позиционной системе с основанием n нужно иметь алфавитиз n цифр. Обычно для этого при n<10 используют n первых арабских цифр, а при n>10 к десяти арабским цифрам добавляют буквы.
Вот примеры алфавитов нескольких систем:
-
Основание
|
Система
|
Алфавит
|
n=2
|
двоичная
|
01
|
n=3
|
троичная
|
01 2
|
n=8
|
восьмеричная
|
01234567
|
n=16
|
шестнадцатеричная
|
0123456789ABCDEF
|
Основание системы, к которой относится число, обозначается подстрочным индексом к этому числу.
1011012, 36718, 3B8F16.
.
Принципы архитектуры ЭВМ были сформулированы Джоном фон Нейманом в 1946 году. Им долгие годы следовали конструкторы ЭВМ. Многие из этих принципов сохранились и в архитектуре современных компьютеров.
Один из этих принципов Неймана:
ЭВМ выполняет арифметические расчеты в двоичной системе счисления.
Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
представление информации посредством только двух состояний надежно и помехоустойчиво;
возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
двоичная арифметика намного проще десятичной.
Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.
Гораздо проще сконструировать процессор, который работает в двоичной системе счисления, чем работающий в десятичной. Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2).
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).
Например:

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.
Например,
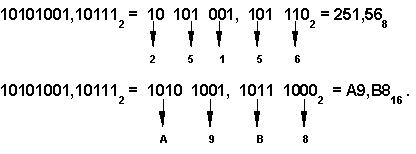
Шестнадцатеричная система счисления используется для компактного представления (на бумаге или на экране) двоичной информации, хранимой в памяти ЭВМ.
Алгоритмы перевода чисел из одной системы счисления в другую.
Мы настолько привыкли к десятичному счету, что число в любой другой системе мало что нам говорит о соответствующем ему количестве. Например, что за величина 1123? Чтобы понять «много это или мало», нужно перевести его в десятичную систему. Сделать это довольно просто.
Число 1123 содержит в себе 2 единицы, 1 тройку и 1 девятку. Как и в десятичной системе, число можно представить в виде суммы произведений составляющих его цифр на соответствующие степени основания системы (в нашем примере — тройки).
1123 =1х32 + 1х31 + 2х3°= 9 + 3 + 2 = 1410
Следовательно, 1123 = 1410
Переведем двоичное число 1011012 в десятичную систему счисления. Принцип тот же. Теперь в сумму надо подставлять степени двойки:
1011012= 1 х 25 + 0 х 24+ 1 х 23 + 1 х 22 + 0 х 21 + 1x2°= 32+ 8 + 4 + 1 = 4510.
И еще один пример — с шестнадцатеричным числом:
15FC16 = 1 х 163 + 5 х 162+ 15 х 161 + 12 = 4096 + 1280 + 240 + 12 = 5628
Аналогично переводятся дробные числа.
101,112 = 1 х 22 + 0 х 21 + 1 х 2° + 1 х 2-1 + 1 х 2-2 =
= 4 + 1 + 1/2 + 1/4 = 5 + 0,5 + 0,25 = 5,7510.
А как произвести обратный перевод из десятичной системы в недесятичную (n≠10)? Для этого нужно суметь разложить десятичное число на слагаемые, содержащие степени n. Например, при n = 2 (двоичная система):
1510 = 8 + 4 + 2 + 1 = 1х23 + 1х22+ 1x21 + 1 = 11112
Эта задача уже посложнее, чем перевод в десятичную систему. Попробуйте, например, таким образом перевести в двоичную систему число 157. Конечно можно, но трудно!
Однако существует процедура, позволяющая легко выполнить такой перевод. Она состоит в том, что данное десятичное число делится с остатком на основание системы. Полученный остаток — это младший разряд искомого числа, а полученное частное снова делится с остатком, который равен второй справа цифре и т.д. Так продолжается до тех пор, пока частное не станет меньше делителя (основания системы). Это частное — старшая цифра искомого числа.
Продемонстрируем этот метод на примере перевода числа 3710 в двоичную систему. Здесь для обозначения цифр в записи числа используется символика: а5а4а3а2а1а0.
Отсюда: 3710 - 1001012
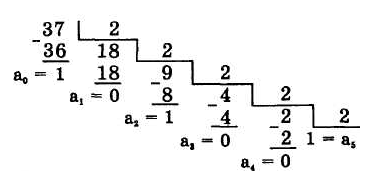
Перевод правильной десятичной дроби в другую систему счисления производится путем последовательных умножений на основание системы с выделением целой части произведений. Однако мы остановимся лишь на целых числах.
Двоичная арифметика.
Вам хорошо знакомы правила выполнения арифметических операций с многозначными десятичными числами. В младших классах школы вы учились складывать, вычитать, умножать «столбиком» и делить «уголком». В конечном счете для выполнения вычислений нужно уметь складывать и умножать однозначные числа. Таблицу умножения десятичных чисел многие первоклассники заучивают долго и с большим трудом. Но вот если бы в школе изучали не десятичную, а двоичную арифметику, проблем бы не было ни у кого и все ученики были бы отличниками! Сейчас вы убедитесь в том, что двоичная арифметика, действительно, очень проста.
С двоичной системой счисления вы уже знакомы. В ней всего две цифры: 0 и 1. Вот все варианты их сложения:
0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 10.
Вам уже должно быть понятно, что 102 = 210 (напомним, что нижний индекс обозначает основание системы счисления и всегда записывается в десятичной системе). Ряд двоичных натуральных чисел легко записать, получая каждое следующее число путем прибавления единицы к предыдущему.
Таблица 1. Десятичные числа от 1 до 16 и равные им двоичные числа
«10»
|
«2»
|
«10»
|
«2»
|
«10»
|
«2»
|
«10»
|
«2»
|
1
|
1
|
5
|
101
|
9
|
1001
|
13
|
1101
|
2
|
10
|
6
|
110
|
10
|
1010
|
14
|
1110
|
3
|
11
|
7
|
111
|
11
|
1011
|
15
|
1111
|
4
|
100
|
8
|
1000
|
12
|
1100
|
16
|
10000
|
Из таблицы 1 видно, как быстро нарастает количество цифр в двоичных числах. Но этот недостаток двоичной системы компенсируется простотой арифметики. Вот пример сложения столбиком двух многозначных двоичных чисел:
1 0 1 1 0 1 1 1 0 1
+1 1 1 0 1 0 1 1 0
1 0 0 1 0 1 1 0 0 1 1
Двоичная таблица умножения:
0 x 0 = 0, 1 x 0 = 0, 1 x 1 = 1.
Пример:
111
х11
 111 111
+ 111
1 0101 0101
5. Вопросы самоконтроля
Чем отличается непрерывный сигнал от дискретного?
Что такое частота дискретизации и на что она влияет?
Объясните понятие информации
Перечислите основные формы представления информации
В чем отличие позиционной и непозиционной систем счисления?
Что такое система счисления?
Что такое основание системы счисления?
Что такое непозиционная система счисления?
Что такое позиционная система счисления?
Из каких знаков состоит алфавит десятичной и двоичной систем?
Почему в вычислительной технике взята за основу двоичная система счисления?
|
 Скачать 3.88 Mb.
Скачать 3.88 Mb.
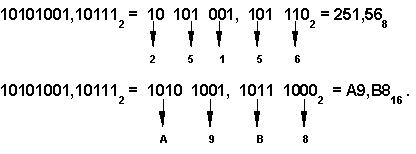

 111
111 0101
0101


