курсач. курсач шамиль. Пояснительная записка проекта включает Литературный обзор
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
2 Расчетная часть 2.1 Технологический расчет Основой технологического расчёта тарельчатых колонн является термодинамический расчёт процессов разделения, который выполняется на базе понятия о теоретической тарелке. Истинное распределение концентраций и потоков по высоте аппарата, оптимальное место ввода питания, количество реальных тарелок и другие показатели, характеризующие работу аппарата, могут быть найдены только при помощи кинетического расчёта, то есть с учётом реально протекающего процесса массопередачи между газом и жидкостью[3]. 2.1.1 Материальный баланс колонны Из уравнений материального баланса колонны по потокам и низкокипящему компоненту (НКК) определяются массовые расходы получаемых дистиллята D и кубового остатка W. 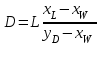 (2.1) (2.1)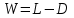 (2.2) (2.2)где L= 22550 кг/час (6,26 кг/с) – массовый расход сырья (т.к в одном часе 3600 с.); yD = 0,97; xW = 0,05; хL = 0,43 – массовые доли НКК соответственно в дистилляте, остатке и сырье. 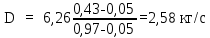 W = 6,26 – 2,58 = 3,68 кг/с 2.1.2 Определение давления и температуры в колонне Давление и температура являются основными параметрами технологического режима в ректификационной колонне. Чем выше принимаемое давление, тем больше должна быть и температура в колонне, так как с повышением давления увеличиваются температуры кипения и конденсации разделяемых смесей. В ректификационных колоннах определяющим параметром является температура, а определяемым – давление. Обычно давление в колонне принимается таким, чтобы пары дистиллята при этом давлении могли быть сконденсированы при помощи наиболее доступных хладагентов, например, воды или воздуха. В первом приближении при выборе давления температуру конденсации паров дистиллята можно принимать не менее чем на 15 – 20о С выше температуры охлаждающего агента на выходе из конденсатора. Температура кипения (конденсации) хлороформа 61,2оС, бензола 80,1оС при атмосферном давлении. Следовательно, процесс ректификации в рассматриваемом случае можно проводить при атмосферном давлении. Согласно заданию курсового проекта, принимаем давление: 1160 мм. рт. ст. 2.1.3 Построение диаграмм фазового равновесия и кривых изобар В случае ректификации бинарных смесей для расчёта числа теоретических тарелок широко используется графический метод, известный в литературе как метод Мак – Кеба и Тиле (диаграмма y – x). Диаграмма кривых изобар позволяет легко определить температуры внешних потоков ректификационной колонны. Кривые равновесия и изобары строятся в пределах температур кипения низкокипящего и высококипящего компонентов при принятом давлении в колонне. В этом интервале температур принимается ряд значений температуры, для каждой температуры определяется по опытным (справочным) данным или рассчитываются (например, по уравнению Антуана) давления насыщенных паров компонентов (или константы фазового равновесия компонентов) [3,6,7]. Далее с использованием законов Рауля и Дальтона рассчитываются концентрации низкокипящего компонента в равновесных жидкой и паровой фазах. Результаты расчёта представляются в виде таблицы. Таблица 2.1 - Координаты кривых равновесия и изобар
В качестве примера приведём расчёты при 77оС. 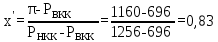 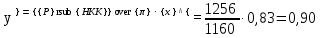 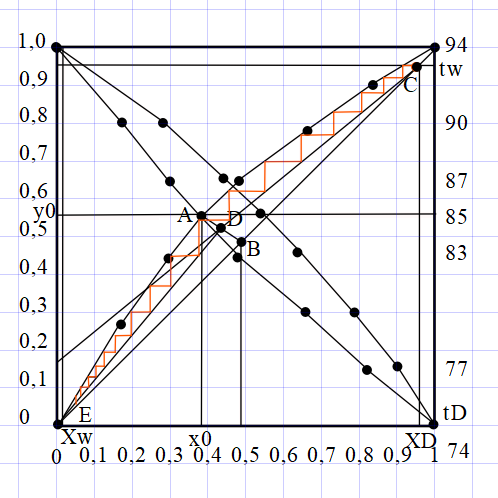 Рисунок 2.1 - Кривые равновесия и изобар. Графическое определение температур внешних потоков и числа теоретических тарелок в колонне. 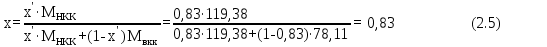 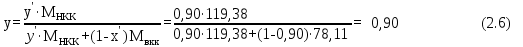 , где Мнкк =119,38; Мвкк = 78,11 – мольные массы хлороформа и бензола При построении кривых равновесия и изобар использованы массовые концентрации (рисунок 2.1). Температура паров дистиллята с верхней тарелки tD=75oC определена из диаграммы t – x,y по верхней кривой (изобара пара), а температура жидкого остатка tW=93oC – по нижней кривой (изобара жидкости). Температура ввода сырья в колонну (tL) при известной доле отгона (е) можно определить при помощи графиков y – x и t – x,y. Для этого из точки В на диагонали диаграммы, абсцисса которой равна составу исходного сырья хL, проводим линию АВ, тангенс угла наклона которой равен 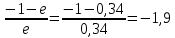 (2.7) (2.7)Эта линия точек пересечения рабочих линий верхней и нижней частей ректификационной колонны. Часто эту линию называют линией питания. Точка пересечения этой линии с кривой равновесия фаз (т. А) определяет составы образовавшихся паровой и жидкой фаз в питательной секции колонны. Откладываем эти значения на графике изобар и определяем температуру ввода сырья tL= 85oC. Примем для расчёта технологическую схему ректификации с острым орошением. Орошение будем подавать в колонну в переохлажденном состоянии. Хладагент - вода, максимальная температура которой 20оС. При разнице температур воды и продукта на холодном конце конденсатора – холодильника, составляющей 15оС, температура в ёмкости орошения, температура холодного орошения будет равна 35оС. 2.1.4 Определение флегмового числа и числа теоретических тарелок Флегмовое число или отношение количества горячего орошения к количеству дистиллята, вместе с числом тарелок является основным параметром, определяющим заданное разделение в процессе ректификации. При увеличении флегмового числа необходимое число тарелок уменьшается, и наоборот. Предельные значения флегмового числа (R=Rmin и R=∞) определяют характерные условия разделения. Минимальное флегмовое число соответствует положению, при котором в каком – либо сечении колонны движущая сила процесса разделения равна нулю. Часто таким сечением является питательная секция колонны. При минимальном флегмовом числе количество тарелок, потребное для разделения, будет равно бесконечности. При бесконечном флегмовом числе, то есть когда нет отбора дистиллята, потребное количество тарелок становится минимальным. Таким образом, предельными условиями работы колонны являются с одной стороны, минимальное флегмовое число при бесконечном количестве тарелок и, с другой стороны, минимальное количество тарелок при бесконечном флегмовом числе. Реальные условия работы колонны соответствуют оптимальному флегмовому числу и оптимальному количеству тарелок. Минимальное флегмовое число при разделении бинарных смесей определяется по уравнению: 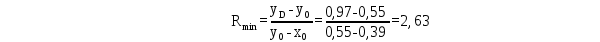 (2.7) (2.7)где уD – содержание НКК в дистилляте; уо и хо – координаты точки пересечения линии питания с кривой равновесия фаз. Оптимальное флегмовое число определяется техноэкономическим расчётом. Для приблизительной его оценки можно воспользоваться рекомендациями Джиллиленда 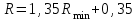 (2.8) (2.8)R = 1,35∙2.63+0,35 = 3.90 Число теоретических тарелок находим графическим путём (смотреть рисунок 2.1). Построение проводим следующим образом. Через точку С, лежащую на диагонали диаграммы у – х проводим рабочую линию верхней части колонны с тангенсом угла наклона 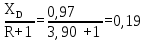 до пересечения с линией питания (точка D). Абсцисса точки С – xD соответствует составу дистиллята yD. Точку D соединяем с точкой Е, лежащей также на диагонали диаграммы и характеризующей состав остатка хw. DE – рабочая линия нижней части колонны. Далее, между равновесной кривой и ломаной линией СDE строим ступенчатую линию. Число теоретических тарелок будет равно числу ступеней изменения концентраций, вписанных между кривой равновесия и ломаной линией. В результате построения получено: вверху колонна имеет 7, а внизу 10 теоретических тарелок. 2.1.5 Тепловой баланс колонны Тепловой баланс колонны составляется с целью определения необходимых затрат тепла и холода. При остром испаряющемся орошении уходящий с верха колонны дистиллят отводится из системы в жидком состоянии. Уравнение теплового баланса для этого случая имеет следующий вид: 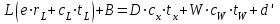 , (2.10) , (2.10)где L,D,W – массовые расходы сырья, дистиллята и остатка, кг/с; rL – теплота испарения сырья, кДж/кг; В – тепло кипятильника, кВт; d’ – тепло отводимое в конденсаторе – холодильнике, кВт. В случае холодного острого орошения, тепло, отводимое в конденсаторе – холодильнике определяется из уравнения теплового баланса верхней части колонны, включающей конденсатор – холодильник и верхнюю тарелку колонны, по уравнению: 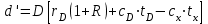 (2.11) (2.11)где rD – теплота испарения (конденсации) паров верха колонны, кДж/кг; сD – удельная теплоёмкость дистиллята при температуре конденсации tD, кДж/кг∙град. Необходимые для расчёта теплофизические свойства индивидуальных компонентов определяются по справочной литературе [3,4,6]. В любом сечении колонны мы имеем смесь компонентов, теплофизические свойства которой зависят от состава смеси и её температуры и определяются по правилу аддитивности. 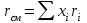 , , 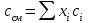 где xi, ri, ci – массовая доля, теплота испарения, удельная теплоёмкость i-того компонента в рассматриваемом сечении при соответствующей температуре. Теплофизические свойства хлороформа и бензола и их смесей, необходимые для расчёта теплового баланса колонны, представлены в таблице 2.2 Таблица 2.2 - Теплофизические свойства хлороформа и бензола
В качестве примера приведём расчёт теплофизических свойств смеси в верхнем сечении колонны при температуре 35 оС. rD = 0,97∙229,52 + 0,03∙487 = 237 кДж/кг (2.12) сD = 0,97∙0,97 + 0,03∙1,76 = 0,99 кДж/кг∙град (2.13) Определим приход и расход тепла с материальными потоками. L∙(e∙rL + cL∙tL) = 6,26∙(0,34∙240 + 1,06∙85) = 1075 кВт (2.14) D∙cx∙tx = 2,58∙0,99∙35 = 90 кВт (2.15) W∙cw∙tw = 3,68∙1,07∙93 = 365 кВт (2.16) Тепло, отводимое в конденсаторе – холодильнике d’=2,58[237∙(1+3,90) + 1,02∙75 – 0,99∙35] = 2830 кВт Количество тепла В, которое необходимо подвести в нижнюю часть колонны через кипятильник, определяется из уравнения общего теплового баланса процесса. B = 90 + 365 + 2830 – 1075 = 2210 кВт (2.17) С учётом тепловых потерь в окружающую среду количество тепла, подводимого в нижнюю часть колонны, увеличим на 10%/ 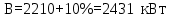 то есть примем В = 2431 кВт. Результаты расчёта теплового баланса сведены в таблицу 2.3. Таблица 2.3 - Тепловой баланс колонны
Количество холодного орошения (Ох) определяется по уравнению: 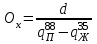 , (2.17) , (2.17)где 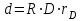 - тепло орошения, кВт; - тепло орошения, кВт;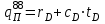 - энтальпия пара, уходящего с верха колонны, кДж/кг; - энтальпия пара, уходящего с верха колонны, кДж/кг;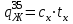 - энтальпия холодного орошения, подаваемого на верхнюю тарелку, кДж/кг. - энтальпия холодного орошения, подаваемого на верхнюю тарелку, кДж/кг.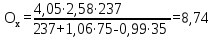 В качестве теплоносителя в кипятильнике колонны принимаем насыщенный водяной пар с абсолютным давлением 3 атм. При этом давлении будет достаточный температурный напор (не менее 15-20 оС). Такой пар имеет температуру 126 оС и теплоту конденсации 2191 кДж/кг. [4, стр.549] Расход водяного пара на подогрев низа колонны определяется по уравнению: 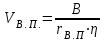 ; (2.18) ; (2.18)где rВ.П – теплота конденсации водяного пара, кДж/кг; η – коэффициент удержания тепла. С учётом коэффициента удержания тепла (в среднем для теплообменников η= 0,95) получим: 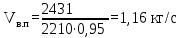 Расход воды в конденсаторе – холодильнике при разности температур охлаждающей воды на входе и выходе из конденсатора – холодильника ∆t =20 оС определим из уравнения: 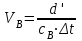 , (2.19) , (2.19)где сВ = 4,19 кДж/кг∙град – удельная теплоёмкость воды. 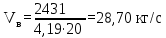 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
