решение задач. Позиционные задачи

• Название: Позиционные задачи
• Анкор: решение задач
• Дата: 26.04.2021
• Размер: 399.36 Kb.
• Имя файла: 438420.docx
• Тип: Глава; #198989

ГЛАВА 1

ПОЗИЦИОННЫЕ ЗАДАЧИ

Позиционными называют задачи, связанные с определением взаимного расположения геометрических фигур. Обычно в этих задачах определяется взаимная принадлежность фигур или строится линия (точки) взаимного пересечения.

Задачи на взаимную принадлежность решаются на основании таких свойств проецирования как: точка принадлежит плоскости, если она принадлежит линии плоскости; прямая линия принадлежит плоскости, если две ее точки принадлежат плоскости, и т.д.

Задачи на взаимное пересечение связаны с построением точек, принадлежащих одновременно двум рассматриваемым геометрическим образам (прямой и плоскости, двум плоскостям, плоскости и поверхности и т.д.).
1.1. Пересечение прямой с плоскостью
Для определения точки пересечения прямой m с плоскостью α (A, B, C) выполняют следующие операции.

Через прямую m проводят проецирующую плоскость β (рис. 1.1). В данном примере проводят горизонтально проецирующую плоскость β′.

Определяют линию n пересечения плоскости β с плоскостью α(ABC). На рис. 1.1 горизонтальная проекция этой линии n′ совпадает с m′ по построению, а фронтальная n′′ − определяется проецированием точек 1′ и 2′ на фронтальные проекции A′′B′′ и B′′C′′ сторон треугольника ABC.



Условие задачи Решение Рис. 3.1

1. 
   Находят точку K пересечения прямой m с плоскостью α. Фронтальная проекция n′′ линии пересечения n пересекает m′′ в точке K′′. Поскольку n лежит в плоскости α, то K принадлежит как плоскости α, так и прямой m, т.е. является точкой их пересечения. Ее горизонтальная проекция K′ определяется проецированием K′′ на m′.
   

Видимость прямой и плоскости относительно горизонтальной плоскости проекций определяется с помощью горизонтально конкурирующих точек 2 и 3. Точка 2 лежит на AC, а 3

− на m. Их фронтальные проекции 2′′ и 3′′ показывают, что точка 2 находится ниже точки 3 и поэтому на горизонтальной плоскости проекций горизонтальная проекция 2′ точки 2 будет закрыта проекцией 3′ точки 3. Отсюда следует, что проекция A′C′ стороны AC расположена ниже проекции m′ и участок этой прямой с левой стороны до K′ будет видимым.

Относительную видимость на фронтальной плоскости проекций можно определить с помощью фронтально конкурирующих точек 4 и 5. Как показывают горизонтальные проекции этих точек 4′ и 5′, точка 4 лежит ближе к наблюдателю, чем точка 5, но поскольку последняя принадлежит прямой m, то участок ее фронтальной проекции 5′′K′′ невидим.

На рис. 3.1.1 дан пример построения точки пересечения прямой AB с плоскостью общего положения α, заданной следами.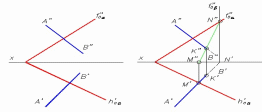



Условие задачи Решение Рис. 3.1.1

В данном случае через прямую AB проведена горизонтально-проецирующая плоскость β. На горизонтальной плоскости проекций линия пересечения плоскостей MN совпадает с горизонтальным следом этой плоскости. Построив фронтальную проекцию прямой M”N” находим фронтальную проекцию точки пересечения ее с прямой AB − K”, после чего по линии связи находим горизонтальную проекцию точки K’. В завершении определяем видимость примой AB относительно точки пересечения.
1.2.Перпендикулярность прямой и плоскости

Прямая перпендикулярна плоскости, если она перпендикулярна двум прямым этой плоскости, например, ее горизонтали и фронтали. Построение перпендикуляра начинают с построения горизонтали и фронтали плоскости (см. рис. 2.18). Затем к этим прямым проводят перпендикуляр так, как это сделано на рис. 2.13.

Прямая n (рис. 3.2) перпендикулярна плоскости α(ABC), так как n ⊥ h и n ⊥ f (на основании свойства 8 ортогонального проецирования − см. раздел 1.2.).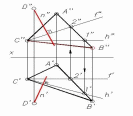



Рис. 3.2

При построении на комплексном чертеже перпендикуляра к плоскости нужно иметь в виду следующее: если n ⊥ α(h ∩ f), то фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали, а его горизонтальная проекция − горизонтальной проекции горизонтали (n’ ⊥ h’; n” ⊥ f”). Действительно и обратное утверждение.

Следует отметить, что полученная таким образом точка пересечения перпендикуляра с фронталью и горизонталью не является точкой пересечения перпендикуляра с плоскостью. Эта точка находится с помощью дополнительных построений (секущих плоскостей), подобно тому, как это было рассмотрено в предыдущем подразделе.

Приведенное решение используется при определении расстояния от точки до плоскости и до других более сложных поверхностей.

Пример: Определить расстояние от точки С до прямой AB (рис. П3.1).

Решение: Расстояние от точки до прямой измеряется натуральной величиной отрезка перпендикуляра, опущенного на нее из этой точки. Поскольку данная прямая − горизонталь, то в соответствии со свойством 8 проецирования прямого угла горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали.

Проводим перпендикуляр из C’ к A’B’, затем строим на его горизонтальной проекции вспомогательный прямоугольный треугольник для определения натуральной величины отрезка перпендикуляра CK.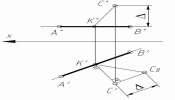

Рис. П3.1

1.3. Перпендикулярность двух плоскостей

Две плоскости взаимно перпендикулярны, если одна из них содержит прямую, перпендикулярную к другой плоскости. Поэтому построение перпендикулярных плоскостей сводится к построению взаимно перпендикулярных прямой и плоскости.

Пример 1: Провести через прямую плоскость, перпендикулярную другой плоскости.

Решение:

На рис. 3.3 рассмотрена задача по проведению через прямую a плоскости γ(a ∩ n), перпендикулярной плоскости α(ABC). Задача сводится к предыдущей, если на прямой a задать точку D и провести через нее перпендикуляр n к плоскости α. Поскольку плоскость γ образована двумя пересекающимися прямыми, одна из которых перпендикулярна α, то, как известно, плоскость, содержащая перпендикуляр к другой плоскости, сама перпендикулярна этой плоскости.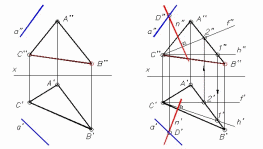


Условие задачи Решение Рис. 3.3

Пример 2: Плоскость α задана следами f ’’₀α и h’α0. Построить плоскость β, перпендикулярную заданной. Плоскость β задать пересекающимися прямыми (рис. 3.4).



Рис. 3.4

Решение:

Проводим прямую l, перпендикулярную плоскости α (l’ ⊥ h’α0 и l” ⊥ f ’’₀α). Затем заключаем эту прямую в какую-либо плоскость. Последняя будет искомой. В данном случае плоскость β задана двумя пересекающимися прямыми, m и l. m − произвольная прямая.

Прямая линия, получаемая при пересечении двух плоскостей, определяется двумя точками, которые принадлежат обеим плоскостям. Из рисунка 3.9 видно, что прямая



Рис. 3.9

MN, по которой пересекаются между собой две плоскости, проходит через точки M и N; но в этих точках прямые AB и AC плоскости треугольника пересекают вторую плоскость, т. е. точки M и N принадлежат обеим плоскостям.

Для нахождения точек пересечения обычно приходится выполнять специальные построения. Но если хотя бы одна из пересекающихся плоскостей перпендикулярна к плоскости проекций, то построение проекций линии пересечения упрощается

Пример:

Дано: Плоскость общего положения α (∆ ABC) и горизонтально-проецирующая плоскость β ⊥

П₁.

Построить линию пересечения этих плоскостей.

Рис. 3.10

Решение

Горизонтально-проецирующая плоскость β проецируется на горизонтальную плоскость проекций в виде прямой линии. На этой же линии находится горизонтальная проекция M’N’ отрезка прямой, по которому пересекаются обе плоскости. С помощью линий связи находим фронтальные проекции точек M” и N”. В завершении определяется видимость сторон треугольника.

Пример:

Дано: Плоскость общего положения (∆ ABC) и следы горизонтально-проецирующей плоскости α (рис. 3.11).

Построить линию пересечения этих плоскостей.

Решение:

Горизонтально-проецирующая плоскость α пересекает плоскость треугольника ABC. Горизонтальная проекция линии пересечения этих плоскостей − отрезок M’N’ определяется на следе α’. Фронтальная проекция линии пересечения строится по линиям связи.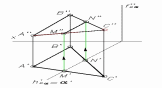


Рис. 3.11

Теперь рассмотрим общий случай построения линии пересечения двух плоскостей. Эта задача решается с использованием вспомогательных секущих плоскостей-посредников, т.е. дополнительно проводят еще две плоскости частного положения, находят линии пересечения этих плоскостей с заданными, а затем строят искомую линию.

Пример: Построить линию пересечения двух плоскостей: плоскость α задана следами, плоскость β задана проекциями треугольника ABC (рис. 3.12).


Рис.3.12 а

Решение:

Линию пересечения можно построить, если найдем две точки K1 и K2, лежащие на ней. Для нахождения точки K1 проведем вспомогательную плоскость γ1  П1. Эта плоскость пересечет плоскость α по горизонтали h₁ (h’₁, h”₁), а плоскость β по горизонтали 1 −2 (1’-2’, 1”2”). Построение проекций видно из чертежа (рис. 3.12, б).


Рис. 3.12, б (решение)

Пересечение горизонталей h и 1−2 даст точку K₁ (K’₁, K”₁), которая принадлежит одновременно трем плоскостям α, β, γ1 и, следовательно, находится на линии пересечения плоскостей α и β.

Для того, чтобы определить K₂, проведем вторую вспомогательную плоскость γ2 и те же построения. Точки K₁ и K₂ определят искомую прямую.

Если плоскости заданы их следами на плоскостях проекций, то естественно искать точки, определяющие прямую пересечения плоскостей, в точках пересечения одноименных следов плоскостей (рис. 3.13): прямая, проходящая через эти точки, является общей для обеих плоскостей, т.е. их линией пересечения.

Точки пересечения одноименных следов плоскостей являются следами линии пересечения этих плоскостей. Поэтому для построения проекций линии пересечения плоскостей α и β надо: 1) найти точку M’ пересечения следов h’₀α и h’₀β и точку N” в пересечении f”₀α и f”₀β, а по ним − проекции M” и N’;

2) провести прямые линии M” N” и M’N’.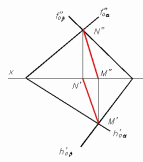



Рис. 3.13

Как отмечено выше, для построения линии пересечения двух плоскостей общего положения используют вспомогательные секущие плоскости. Если плоскости представлены в виде многоугольников, то в этом случае находят точки пересечения прямых, принадлежащих одной плоскости, с другой плоскостью. Таким образом, если плоскости заданы треугольниками, нужно найти точку пересечения одной стороны треугольника с плоскостью общего положения, которой является второй треугольник, затем найти точку пересечения второй стороны треугольника с той же плоскостью общего положения. Соединив эти точки прямой линией, получим прямую, по которой пересекаются треугольники (рис. 3.7).

Как правило, в качестве секущих плоскостей используют плоскости частного положения

− фронтально-проецирующие, либо горизонтально-проецирующие.



Рис. 3.7

Определение: Прямая параллельна плоскости, если в плоскости можно провести прямую, ей параллельную.

Пример: Через точку D провести прямую, параллельную плоскости треугольника ABC. Решение: Построение следует начинать с проведения в плоскости треугольника ABC произвольной прямой (например, горизонтали h, рис 3.5), затем через точку D проводят прямую l, параллельную h.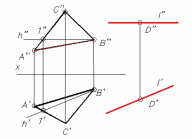

Рис. 3.5

Иногда бывает необходимо проверить параллельность прямой m заданной плоскости. Для этого в какой-либо проекции плоскости проводят прямую, параллельную соответствующей проекции прямой m, а затем проверяют параллельность других проекций.