Практическая работа Построение статических и динамических моделей. Построение эмпирических моделей. Линейный регрессионный анализ для построения эмпирических моделей
 Скачать 0.78 Mb.
|
Метод наименьших квадратов (МНК).Пример. Экспериментальные данные о значениях переменных х и у приведены в таблице. 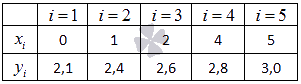 В результате их выравнивания получена функция  Используя метод наименьших квадратов , аппроксимировать эти данные линейной зависимостью y=ax+b (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж. Суть метода наименьших квадратов (МНК).Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b  принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов. Таким образом, решение примера сводится к нахождению экстремума функции двух переменных. Вывод формул для нахождения коэффициентов.Составляется и решается система из двух уравнений с двумя неизвестными. Находим частные производные функции 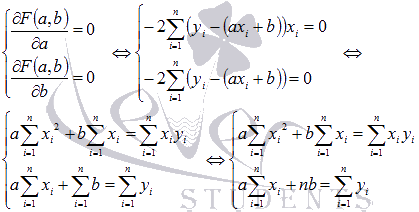по переменным а и b, приравниваем эти производные к нулю. Решаем полученную систему уравнений любым методом (например методом подстановки или методом Крамера) и получаем формулы для нахождения коэффициентов по методу наименьших квадратов (МНК). 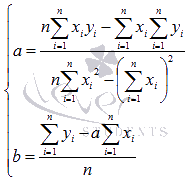 При данных а и b функция принимает наименьшее значение. Доказательство этого факта приведено ниже по тексту в конце страницы . Вот и весь метод наименьших квадратов. Формула для нахождения параметра a содержит суммы  ,  ,  ,  и параметр n - количество экспериментальных данных. Значения этих сумм рекомендуем вычислять отдельно. Коэффициент b находится после вычисления a. Пришло время вспомнить про исходый пример. Решение. В нашем примере n=5 . Заполняем таблицу для удобства вычисления сумм, которые входят в формулы искомых коэффициентов. 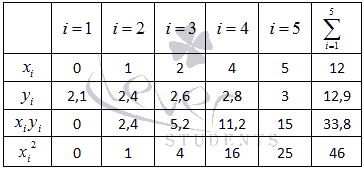 Значения в четвертой строке таблицы получены умножением значений 2-ой строки на значения 3-ей строки для каждого номера i . Значения в пятой строке таблицы получены возведением в квадрат значений 2-ой строки для каждого номера i . Значения последнего столбца таблицы – это суммы значений по строкам. Используем формулы метода наименьших квадратов для нахождения коэффициентов а и b. Подставляем в них соответствующие значения из последнего столбца таблицы: 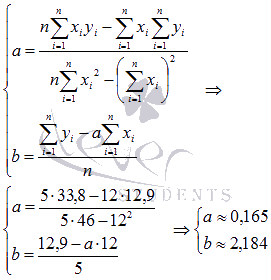 Следовательно, y = 0.165x+2.184 - искомая аппроксимирующая прямая. Осталось выяснить какая из линий y = 0.165x+2.184 или лучше аппроксимирует исходные данные, то есть произвести оценку методом наименьших квадратов. Оценка погрешности метода наименьших квадратов.Для этого требуется вычислить суммы квадратов отклонений исходных данных от этих линий 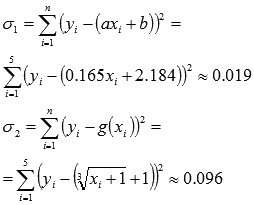 и  , меньшее значение соответствует линии, которая лучше в смысле метода наименьших квадратов аппроксимирует исходные данные. Так как  , то прямая y = 0.165x+2.184 лучше приближает исходные данные. |