Практическая работа Построение статических и динамических моделей. Построение эмпирических моделей. Линейный регрессионный анализ для построения эмпирических моделей
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
|
Практическая работа № 1. Построение статических и динамических моделей. Построение эмпирических моделей. Линейный регрессионный анализ для построения эмпирических моделей. Данная практическая работа выполняется методом творческих заданий. На примере, разбираемом на практическом занятии, студенты учатся анализировать экспериментальные данные, находить математические зависимости. В качестве творческих заданий предлагаются таблицы экспериментальных данных, полученных студентами заранее во время занятий научной работой. При решении творческих заданий, студенты могут выполнять роль экспертов, помогая другим студентам в группе найти правильное решение. Экспертами выбираются студенты, быстро построившие модель процесса. Регрессионный анализ позволяет оценить степень связи между переменными, предлагая механизм вычисления предполагаемого значения переменной из нескольких уже известных значений. Используя регрессионный анализ, можно продлить линию тренда в диаграмме за пределы реальных данных для предсказания будущих значений. Описание последовательности действий при моделировании: Полученные в результате эксперимента данные зависимости между величинами х и у можно представить в виде таблицы 1: Таблица 1-Экспериментальные данные
Необходимо найти эмпирическую формулу y = f(x), связывающую между собой соответствующие значения переменных так, чтобы значения этой функции при x = xi возможно мало отличались бы от yi, полученных из опыта. Цели работы: 1) построить математическую модель в виде эмпирической формулы; 2) сделать оценку параметров модели; 3) проверить модель на адекватность. Выбор общего вида эмпирической формулы может быть произведен на основе теоретических представлений о характере изучаемой зависимости. В других случаях приходится подбирать формулу, сравнивая кривую, построенную по данным наблюдений с типичными графиками формул. Такими графиками могут служить линии тренда, которые можно добавить на диаграмму Microsoft Excel. Линия тренда – это графическое представление направления изменения ряда данных. Линии тренда используются для анализа ошибок предсказания. Точность аппроксимации. Линия тренда в наибольшей степени приближается к представленной на диаграмме зависимости, если значение R-квадрат равно или близко к 1. При аппроксимации данных с помощью линии тренда значение R-квадрат рассчитывается автоматически. Полученный результат можно вывести на диаграмме. При этом можно использовать следующие функциональные зависимости: Линейная: Y = a + bx, где a –координата пересечения оси абсцисс и b –угол наклона константы; Логарифмическая: Y = clnx + b, где c и b – константы, ln – функция натурального логарифма. Экспоненциальная: Y = cеbx, где c и b – константы, e – основание натурального логарифма. Степенная: Y = cxb, где c и b – константы; Полиномиальная: Y = b + c1x +c2x2 + c3x3+ … + c6x6,где b и c1 … c6 – константы. Величина достоверности аппроксимации – R. Число от 0 до 1, которое отражает близость значений линии тренда к фактическим данным. Линия тренда наиболее соответствует действительности, когда значение R в квадрате близко к 1. Оно также называется квадратом смешанной корреляции. Классический подход к оцениванию параметров линейной регрессии Y =a + bx основан на методе наименьших квадратов, который позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений Y результативного признака от расчетных (теоретических) f(х) будет минимальна: ОШ= f(х)-Ymin, ОШлин = (fлин (xi)-yi)2; ОШэксп= (fэксп (xi) -yi)2; ОШлог= (fлог (xi)-yi)2. т.е. из всего множества линий регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной. Средняя квадратическая ошибка вычисляется по формуле: Методика выполнения работы 1. Оформить исходные данные в виде сводной таблицы Microsoft Excel. 2. С помощью Мастера диаграмм M. Excel построить график зависимости всего диапазона данных сводной таблицы. 3. Построить линию тренда. 4. Для полученных математических моделей сделать оценку параметров: а) провести вычисление средней квадратичной ошибки δ; б) сравнить δ с величиной достоверности аппроксимации – R. 5. Проверить модель на адекватность. Функция, которой соответствует минимальное значение δ и максимальное значение R, является математической моделью, наиболее близко описывающей исходные данные. Пример 1: Проведено исследование зависимости функционально-технологических свойств (показателя активной кислотности рН и щелочности) водно-спиртовых смесей от вариации объемных долей спирта V1 и воды V2 (V1+ V2 = 100 мл). В результате эксперимента были получены следующие зависимости (таблица 2). Таблица 2 - Зависимость щелочности и показателя активной кислотности рН от объемной доли спирта
Необходимо построить различные виды зависимостей рН и щелочности спирта от объемной доли спирта в водно-спиртовой смеси и выбрать уравнение линии тренда наиболее соответствующее действительности для предсказания будущих значений. Решение задачи Осуществим выбор прогнозной модели, позволяющей наиболее точно указать зависимость уровня рН водно-спиртовой смеси от объемной доли спирта. Для этого построим зависимость величины Y1отV1(рис.1). 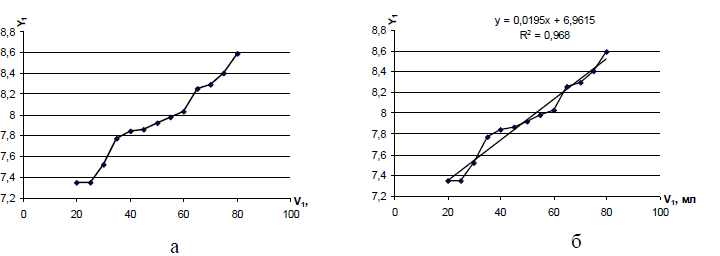 Рисунок 1 – График зависимости рН от объемной доли спирта (Х – объемная доля спирта, Y – уровень рН): а – без линии тренда, б – с линией линейного тренда Добавим к построенному графику линию тренда, которая позволяет однозначно определить характер наблюдаемой динамики (рис. 2, 3). 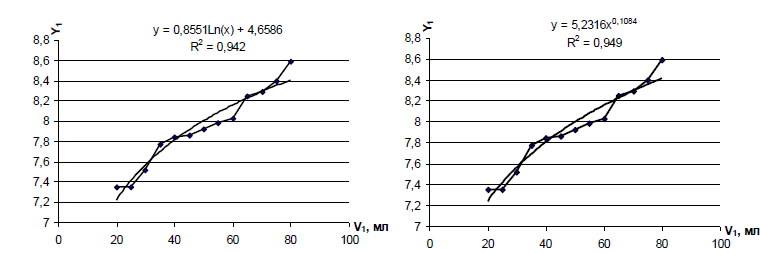 Рисунок 2 – Логарифмический тренд Рисунок 3 – Степенной тренд Итак, по значению коэффициента детерминации R2 (квадрата корреляции) наиболее значимой оказывается линейная линия тренда (для данной модели R2 принимает наибольшее значение). Получаем математические модели: fлин(x) = 0,0195x +6,9615; fэксп(xi) =5,2316x0,1084; fлог(xi) = 0,8551Ln(x)+4,6586. 2. Для полученных моделей оценим параметры: а) проведем вычисление средней квадратичной ошибки δ; ОШлин = (fлин (xi)-yi)2; ОШэксп= (fэксп (xi) -yi)2; ОШлог= (fлог (xi)-yi)2. 3. Сравним значения δ полученных формул и величины достоверности аппроксимации – R. Приходим к выводу, что наилучшим образом исходные данные описывает линейная регрессионная модель. Для того чтобы «улучшить» построенную эмпирическую зависимость построим полиноминальную зависимость 6-й степени. Зависимость y = 2E-09x6 - 7E-07x5 + 8E-05x4 - 0,0053x3 + 0,1844x2 - 3,1966x + 28,928 имеет большой коэффициент детерминации R2= 0,9958 (т.е. доля вариации величины рН уже на 99,58% будет объясняться вариацией объемной долей спирта в водно-спиртовой смеси). Регрессионно-факторный анализ технологических моделей. Данная практическая работа выполняется методом творческих заданий. Предлагается использовать таблицы экспериментальных данных, полученных студентами заранее во время занятий научной работой. При решении творческих заданий, студенты могут выполнять роль экспертов, помогая другим студентам в группе найти правильное решение. Экспертами выбираются студенты, быстро построившие модель процесса. Регрессионный анализ позволяет оценить степень связи между переменными, предлагая механизм вычисления предполагаемого значения y = 0,8551Ln(x) + 4,6586 переменной из нескольких уже известных значений. В состав M. Excel входит набор средств анализа данных (пакет анализа), предназначенный для решения сложных статистических и инженерных задач. Для анализа данных следует указать входные данные и выбрать параметры; анализ будет выполнен с помощью подходящей статистической или инженерной макрофункции, а результат будет помещен в выходной диапазон. Другие средства позволяют представить результаты анализа в графическом виде. Средства, включенные в пакет анализа данных, доступны через команду Анализ данных меню Сервис. Если этой команды нет в меню, необходимо загрузить надстройку Пакет анализа. Цель работы: проанализировать влияние функционально-технологических свойств рецептурных смесей на основе регрессионно-факторного анализа. Пример: В лабораторных условиях было исследовано влияние ферментного препарата глюкозооксидазы (х2) в сочетании с аскорбиновой кислотой (х1) на качество хлеба (табл.). Необходимо с помощью ЭВМ расчитать, какой фактор (х1 илих2) оказывает большее влияние на пористость хлеба; построить эмпирическую линейную модель зависимости пористости хлеба y от фактора х1 или х2, оказывающего на него большее влияние; выявить, как изменится пористость хлеба, если величину глюкозооксидазы увеличить на 30% от среднего значения выборки. Таблица 3- Влияние ферментного препарата глюкозооксидазы в сочетании с аскорбиновой кислотой на качество хлеба
1. Создадим шаблон-таблицу в M. Excel. 2. Определим, какой фактор (количество аскорбиновой кислоты х1 или количество глюкозооксидазы х2) оказывает большее влияние на пористость хлеба с помощью коэффициента регрессии. Для этого построим матрицу коэффициентов корреляции: Сервис → Анализ данных → Корреляция (рис. 4). 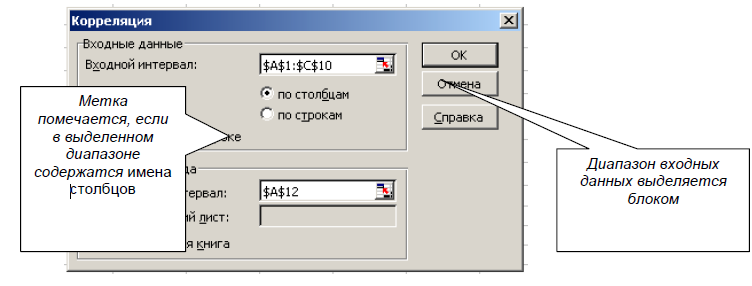 Рисунок 4 – Определение матрицы коэффициентов корреляции Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть, большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция), или, наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (нулевая корреляция). Коэффициент корреляции, как ковариационный анализ, характеризует область, в которой два измерения изменяются вместе. Коэффициент масштабируется таким образом, что его значение не зависит от единиц, в которых выражены переменные двух измерений. Таблица 4- Матрица коэффициентов корреляции
Любое значение коэффициента корреляции должно находится в диапазоне от –1 до +1 включительно. Чем ближе по модулю коэффициент корреляции rхук 1, тем теснее связь между х и у. Если │rх1у│>│rх2у│, то фактор х1 оказывает большее влияние на у, чем х2. В результате имеем: rх1у = 0,304572452 – связь (между х1 и у) слабая; rх2у = -0,88317– связь (между х2 и у) умеренная обратная (т.е. с увеличением количества глюкооксидазы, пористость хлеба уменьшается). Значит │rх1у│<│rх2у│, поэтому фактор х1 оказывает меньшее влияние на у, чем х2. Следовательно, будем строить эмпирическую зависимость Метка помечается, если в выделенном диапазоне содержатся имена столбцов Диапазон входных данных выделяется блоком пористости хлеба у от количества глюкооксидазы х2. Построим эмпирическую модель зависимости пористости хлеба у от количества глюкооксидазы х2. Для этого используем встроенный пакет регрессионного анализа: Сервис → Анализ данных → Регрессия (рис. 5). 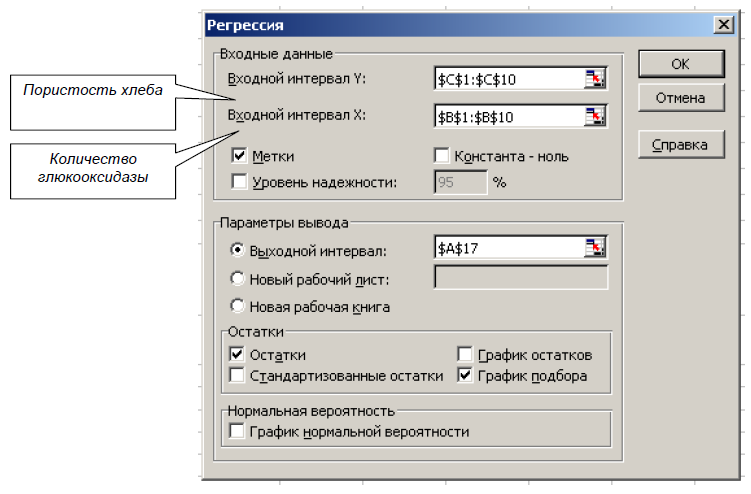 Рисунок 5 – Вид окна пакета «Регрессия» Линейный регрессионный анализ заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Получили зависимость: y=87,3– 29,1х2. Коэффициент детерминации R2=0,78, т.е. доля вариации у объясняется лишь на 78% вариацией (есть смысл «улучшить» модель для вычисления значения). |
