Практическая работа Построение статических и динамических моделей. Построение эмпирических моделей. Линейный регрессионный анализ для построения эмпирических моделей

• Название: Практическая работа Построение статических и динамических моделей. Построение эмпирических моделей. Линейный регрессионный анализ для построения эмпирических моделей
• Анкор: PR_1.doc
• Дата: 06.05.2018
• Размер: 0.78 Mb.
• Имя файла: PR_1.doc
• Тип: Практическая работа; #18956
• страница: 3 из 3

Графическая иллюстрация метода наименьших квадратов (мнк).

На графиках все прекрасно видно. Красная линия – это найденная прямая y = 0.165x+2.184, синяя линия – это 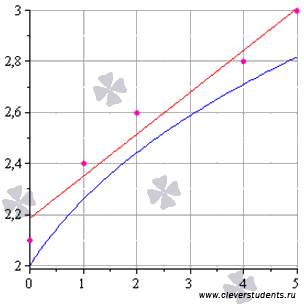, розовые точки – это исходные данные.


На практике при моделировании различных процессов - в частности, экономических, физических, технических, социальных - широко используются те или иные способы вычисления приближенных значений функций по известным их значениям в некоторых фиксированных точках.

 

Такого рода задачи приближения функций часто возникают:

• 
  при построении приближенных формул для вычисления значений характерных величин исследуемого процесса по табличным данным, полученным в результате эксперимента;
  
• 
  при численном интегрировании, дифференцировании, решении дифференциальных уравнений и т. д.;
  
• 
  при необходимости вычисления значений функций в промежуточных точках рассматриваемого интервала;
  
• 
  при определении значений характерных величин процесса за пределами рассматриваемого интервала, в частности при прогнозировании.
  

Если для моделирования некоторого процесса, заданного таблицей, построить функцию, приближенно описывающую данный процесс на основе метода наименьших квадратов, она будет называться аппроксимирующей функцией (регрессией), а сама задача построения аппроксимирующих функций - задачей аппроксимации.

 

В данной статье рассмотрены возможности пакета MS Excel для решения такого рода задач, кроме того, приведены методы и приемы построения (создания) регрессий для таблично заданных функций (что является основой регрессионного анализа).

 

В Excel для построения регрессий имеются две возможности.

1. 
   Добавление выбранных регрессий (линий тренда - trendlines) в диаграмму, построенную на основе таблицы данных для исследуемой характеристики процесса (доступно лишь при наличии построенной диаграммы);
   
2. 
   Использование встроенных статистических функций рабочего листа Excel, позволяющих получать регрессии (линии тренда) непосредственно на основе таблицы исходных данных.
   

Добавление линий тренда в диаграмму

 

Для таблицы данных, описывающих некоторый процесс и представленных диаграммой, в Excel имеется эффективный инструмент регрессионного анализа, позволяющий:

• 
  строить на основе метода наименьших квадратов и добавлять в диаграмму пять типов регрессий, которые с той или иной степенью точности моделируют исследуемый процесс;
  
• 
  добавлять к диаграмме уравнение построенной регрессии;
  
• 
  определять степень соответствия выбранной регрессии отображаемым на диаграмме данным.
  

На основе данных диаграммы Excel позволяет получать линейный, полиномиальный, логарифмический, степенной, экспоненциальный типы регрессий, которые задаются уравнением:


y = y(x)

 

где x - независимая переменная, которая часто принимает значения последовательности натурального ряда чисел (1; 2; 3; …) и производит, например, отсчет времени протекания исследуемого процесса (характеристики).

 

1. Линейная регрессия хороша при моделировании характеристик, значения которых увеличиваются или убывают с постоянной скоростью. Это наиболее простая в построении модель исследуемого процесса. Она строится в соответствии с уравнением:


y = mx + b

 

где m - тангенс угла наклона линейной регрессии к оси абсцисс; b - координата точки пересечения линейной регрессии с осью ординат.

 

2. Полиномиальная линия тренда полезна для описания характеристик, имеющих несколько ярко выраженных экстремумов (максимумов и минимумов). Выбор степени полинома определяется количеством экстремумов исследуемой характеристики. Так, полином второй степени может хорошо описать процесс, имеющий только один максимум или минимум; полином третьей степени - не более двух экстремумов; полином четвертой степени - не более трех экстремумов и т. д.

 

В этом случае линия тренда строится в соответствии с уравнением:


y = c0 + c1x + c2x2 + c3x3 + c4x4 + c5x5 + c6x6

 

где коэффициенты c0, c1, c2,... c6 - константы, значения которых определяются в ходе построения.

 

3. Логарифмическая линия тренда с успехом применяется при моделировании характеристик, значения которых вначале быстро меняются, а затем постепенно стабилизируются.

 

Строится в соответствии с уравнением:


y = c ln(x) + b

 

где коэффициенты b, с - константы.

 

4. Степенная линия тренда дает хорошие результаты, если значения исследуемой зависимости характеризуются постоянным изменением скорости роста. Примером такой зависимости может служить график равноускоренного движения автомобиля. Если среди данных встречаются нулевые или отрицательные значения, использовать степенную линию тренда нельзя.

 

Строится в соответствии с уравнением:


y = c xb

 

где коэффициенты b, с - константы.

 

5. Экспоненциальную линию тренда следует использовать в том случае, если скорость изменения данных непрерывно возрастает. Для данных, содержащих нулевые или отрицательные значения, этот вид приближения также неприменим.

 

Строится в соответствии с уравнением:


y = c ebx

 

где коэффициенты b, с - константы.

 

При подборе линии тренда Excel автоматически рассчитывает значение величины R2, которая характеризует достоверность аппроксимации: чем ближе значение R2 к единице, тем надежнее линия тренда аппроксимирует исследуемый процесс. При необходимости значение R2 всегда можно отобразить на диаграмме.

 

Определяется по формуле: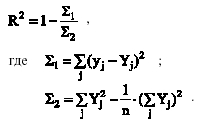

 



 Для добавления линии тренда к ряду данных следует:

• 
  активизировать построенную на основе ряда данных диаграмму, т. е. щелкнуть в пределах области диаграммы. В главном меню появится пункт Диаграмма;
  
• 
  после щелчка на этом пункте на экране появится меню, в котором следует выбрать команду Добавить линию тренда.
  

Эти же действия легко реализуются, если навести указатель мыши на график, соответствующий одному из рядов данных, и щелкнуть правой кнопкой мыши; в появившемся контекстном меню выбрать команду Добавить линию тренда. На экране появится диалоговое окно Линия тренда с раскрытой вкладкой Тип (рис. 1).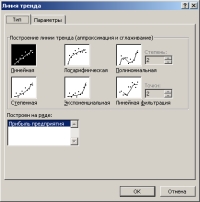

 



 

После этого необходимо:

 

Выбрать на вкладке Тип необходимый тип линии тренда (по умолчанию выбирается тип Линейный). Для типа Полиномиальная в поле Степень следует задать степень выбранного полинома.


1. В поле Построен на ряде перечислены все ряды данных рассматриваемой диаграммы. Для добавления линии тренда к конкретному ряду данных следует в поле Построен на ряде выбрать его имя.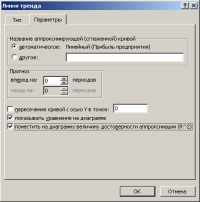

 



 

При необходимости, перейдя на вкладку Параметры (рис. 2), можно для линии тренда задать следующие параметры:

• 
  изменить название линии тренда в поле Название аппроксимирующей (сглаженной) кривой.
  
• 
  задать количество периодов (вперед или назад) для прогноза в поле Прогноз;
  
• 
  вывести в область диаграммы уравнение линии тренда, для чего следует включить флажок показать уравнение на диаграмме;
  
• 
  вывести в область диаграммы значение достоверности аппроксимации R2, для чего следует включить флажок поместить на диаграмму величину достоверности аппроксимации (R^2);
  
• 
  задать точку пересечения линии тренда с осью Y, для чего следует включить флажок пересечение кривой с осью Y в точке;
  
• 
  щелкнуть на кнопке OK, чтобы закрыть диалоговое окно.
  

Для того, чтобы начать редактирование уже построенной линии тренда, существует три способа:

1. 
   воспользоваться командой Выделенная линия тренда из меню Формат, предварительно выбрав линию тренда;
   
2. 
   выбрать команду Формат линии тренда из контекстного меню, которое вызывается щелчком правой кнопки мыши по линии тренда;
   
3. 
    двойным щелчком по линии тренда.
   

На экране появится диалоговое окно Формат линии тренда (рис. 3), содержащее три вкладки: Вид, Тип, Параметры, причем содержимое последних двух полностью совпадает с аналогичными вкладками диалогового окна Линия тренда (рис.1-2). На вкладке Вид, можно задать тип линии, ее цвет и толщину.

 



 

Для удаления уже построенной линии тренда следует выбрать удаляемую линию тренда и нажать клавишу Delete.

 

Достоинствами рассмотренного инструмента регрессионного анализа являются:

• 
  относительная легкость построения на диаграммах линии тренда без создания для нее таблицы данных;
  
• 
  достаточно широкий перечень типов предложенных линий трендов, причем в этот перечень входят наиболее часто используемые типы регрессии;
  
• 
  возможность прогнозирования поведения исследуемого процесса на произвольное (в пределах здравого смысла) количество шагов вперед, а также назад;
  
• 
  возможность получения уравнения линии тренда в аналитическом виде;
  
• 
  возможность, при необходимости, получения оценки достоверности проведенной аппроксимации.
  

К недостаткам можно отнести следующие моменты:

• 
  построение линии тренда осуществляется лишь при наличии диаграммы, построенной на ряде данных;
  
• 
  процесс формирования рядов данных для исследуемой характеристики на основе полученных для нее уравнений линий тренда несколько загроможден: искомые уравнения регрессий обновляются при каждом изменении значений исходного ряда данных, но только в пределах области диаграммы, в то время как ряд данных, сформированный на основе старого уравнения линии тренда, остается без изменения;
  
• 
  в отчетах сводных диаграмм при изменении представления диаграммы или связанного отчета сводной таблицы имеющиеся линии тренда не сохраняются, то есть до проведения линий тренда или другого форматирования отчета сводных диаграмм следует убедиться, что макет отчета удовлетворяет необходимым требованиям.
  

Линиями тренда можно дополнить ряды данных, представленные на диаграммах типа график, гистограмма, плоские ненормированные диаграммы с областями, линейчатые, точечные, пузырьковые и биржевые.

 

Нельзя дополнить линиями тренда ряды данных на объемных, нормированных, лепестковых, круговых и кольцевых диаграммах.

 

Использование встроенных функций Excel

 

В Excel имеется также инструмент регрессионного анализа для построения линий тренда вне области диаграммы. Для этой цели можно использовать ряд статистических функций рабочего листа, однако все они позволяют строить лишь линейные или экспоненциальные регрессии.

 

В Excel имеется несколько функций для построения линейной регрессии, в частности:

• 
  ТЕНДЕНЦИЯ;
  
• 
  ЛИНЕЙН;
  
• 
  НАКЛОН и ОТРЕЗОК.
  

А также несколько функций для построения экспоненциальной линии тренда, в частности:

• 
  РОСТ;
  
• 
  ЛГРФПРИБЛ.
  

Следует отметить, что приемы построения регрессий с помощью функций ТЕНДЕНЦИЯ и РОСТ практически совпадают. То же самое можно сказать и о паре функций ЛИНЕЙН и ЛГРФПРИБЛ. Для четырех этих функций при создании таблицы значений используются такие возможности Excel, как формулы массивов, что несколько загромождает процесс построения регрессий. Заметим также, что построение линейной регрессии, на наш взгляд, легче всего осуществить с помощью функций НАКЛОН и ОТРЕЗОК, где первая из них определяет угловой коэффициент линейной регрессии, а вторая - отрезок, отсекаемый регрессией на оси ординат.

 

Достоинствами инструмента встроенных функций для регрессионного анализа являются:

• 
  достаточно простой однотипный процесс формирования рядов данных исследуемой характеристики для всех встроенных статистических функций, задающих линии тренда;
  
• 
  стандартная методика построения линий тренда на основе сформированных рядов данных;
  
• 
  возможность прогнозирования поведения исследуемого процесса на необходимое количество шагов вперед или назад.
  

А к недостаткам относится то, что в Excel нет встроенных функций для создания других (кроме линейного и экспоненциального) типов линий тренда. Это обстоятельство часто не позволяет подобрать достаточно точную модель исследуемого процесса, а также получить близкие к реальности прогнозы. Кроме того, при использовании функций ТЕНДЕНЦИЯ и РОСТ не известны уравнения линий тренда.

 

Следует отметить, что авторы не ставили целью статьи изложение курса регрессионного анализа с той или иной степенью полноты. Основная ее задача - на конкретных примерах показать возможности пакета Excel при решении задач аппроксимации; продемонстрировать, какими эффективными инструментами для построения регрессий и прогнозирования обладает Excel; проиллюстрировать, как относительно легко такие задачи могут быть решены даже пользователем, не владеющим глубокими знаниями регрессионного анализа.

 

Примеры решения конкретных задач

 

Рассмотрим решение конкретных задач с помощью перечисленных инструментов пакета Excel.

 

Задача 1

 

С таблицей данных о прибыли автотранспортного предприятия за 1995-2002 гг. необходимо выполнить следующие действия.

1. 
   Построить диаграмму.
   
2. 
   В диаграмму добавить линейную и полиномиальную (квадратичную и кубическую) линии тренда.
   
3. 
   Вывести уравнения полученных линий тренда, а также величины достоверности аппроксимации R2 для каждой из них.
   
4. 
   Используя уравнения линий тренда, получить табличные данные по прибыли предприятия для каждой линии тренда за 1995-2004 г.г.
   
5. 
   Составить прогноз по прибыли предприятия на 2003 и 2004 гг.
   

Решение задачи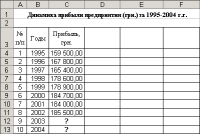

 

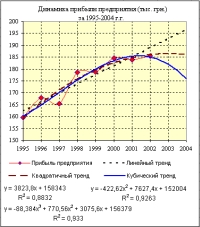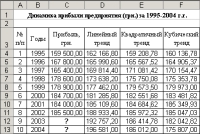1. 
   В диапазон ячеек A4:C11 рабочего листа Excel вводим рабочую таблицу, представленную на рис. 4.
   
2. 
   Выделив диапазон ячеек В4:С11, строим диаграмму.
   
3. 
   Активизируем построенную диаграмму и по описанной выше методике после выбора типа линии тренда в диалоговом окне Линия тренда (см. рис. 1) поочередно добавляем в диаграмму линейную, квадратичную и кубическую линии тренда. В этом же диалоговом окне открываем вкладку Параметры (см. рис. 2), в поле Название аппроксимирующей (сглаженной) кривой вводим наименование добавляемого тренда, а в поле Прогноз вперед на: периодов задаем значение 2, так как планируется сделать прогноз по прибыли на два года вперед. Для вывода в области диаграммы уравнения регрессии и значения достоверности аппроксимации R2 включаем флажки показывать уравнение на экране и поместить на диаграмму величину достоверности аппроксимации (R^2). Для лучшего визуального восприятия изменяем тип, цвет и толщину построенных линий тренда, для чего воспользуемся вкладкой Вид диалогового окна Формат линии тренда (см. рис. 3). Полученная диаграмма с добавленными линиями тренда представлена на рис. 5.
   
4. 
   Для получения табличных данных по прибыли предприятия для каждой линии тренда за 1995-2004 гг. воспользуемся уравнениями линий тренда, представленными на рис. 5. Для этого в ячейки диапазона D3:F3 вводим текстовую информацию о типе выбранной линии тренда: Линейный тренд, Квадратичный тренд, Кубический тренд. Далее вводим в ячейку D4 формулу линейной регрессии и, используя маркер заполнения, копируем эту формулу c относительными ссылками в диапазон ячеек D5:D13. Следует отметить, что каждой ячейке с формулой линейной регрессии из диапазона ячеек D4:D13 в качестве аргумента стоит соответствующая ячейка из диапазона A4:A13. Аналогично для квадратичной регрессии заполняется диапазон ячеек E4:E13, а для кубической регрессии - диапазон ячеек F4:F13. Таким образом, составлен прогноз по прибыли предприятия на 2003 и 2004 гг. с помощью трех трендов. Полученная таблица значений представлена на рис. 6.
   

     

 

Задача 2

 

С таблицей данных о прибыли автотранспортного предприятия за 1995-2002 гг., приведенной в задаче 1, необходимо выполнить следующие действия.

1. 
   Построить диаграмму.
   
2. 
   В диаграмму добавить логарифмическую, степенную и экспоненциальную линии тренда.
   
3. 
   Вывести уравнения полученных линий тренда, а также величины достоверности аппроксимации R2 для каждой из них.
   
4. 
   Используя уравнения линий тренда, получить табличные данные о прибыли предприятия для каждой линии тренда за 1995-2002 гг.
   
5. 
   Составить прогноз о прибыли предприятия на 2003 и 2004 гг., используя эти линии тренда.
   

Решение задачи

 

Следуя методике, приведенной при решении задачи 1, получаем диаграмму с добавленными в нее логарифмической, степенной и экспоненциальной линиями тренда (рис. 7). Далее, используя полученные уравнения линий тренда, заполняем таблицу значений по прибыли предприятия, включая прогнозируемые значения на 2003 и 2004 гг. (рис. 8).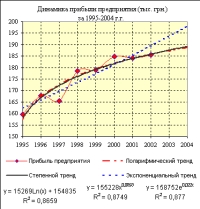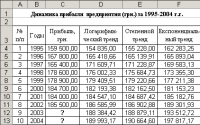

 

    

 

На рис. 5 и рис. видно, что модели с логарифмическим трендом, соответствует наименьшее значение достоверности аппроксимации

 

R2 = 0,8659

 

Наибольшие же значения R2 соответствуют моделям с полиномиальным трендом: квадратичным (R2 = 0,9263) и кубическим (R2 = 0,933).

 

Задача 3

 

С таблицей данных о прибыли автотранспортного предприятия за 1995-2002 гг., приведенной в задаче 1, необходимо выполнить следующие действия.

1. 
   Получить ряды данных для линейной и экспоненциальной линии тренда с использованием функций ТЕНДЕНЦИЯ и РОСТ.
   
2. 
   Используя функции ТЕНДЕНЦИЯ и РОСТ, составить прогноз о прибыли предприятия на 2003 и 2004 гг.
   
3. 
   Для исходных данных и полученных рядов данных построить диаграмму.
   

Решение задачи

 

Воспользуемся рабочей таблицей задачи 1 (см. рис. 4). Начнем с функции ТЕНДЕНЦИЯ:

1. 
   выделяем диапазон ячеек D4:D11, который следует заполнить значениями функции ТЕНДЕНЦИЯ, соответствующими известным данным о прибыли предприятия;
   
2. 
   вызываем команду Функция из меню Вставка. В появившемся диалоговом окне Мастер функций выделяем функцию ТЕНДЕНЦИЯ из категории Статистические, после чего щелкаем по кнопке ОК. Эту же операцию можно осуществить нажатием кнопки (Вставка функции) стандартной панели инструментов.
   
3. 
   В появившемся диалоговом окне Аргументы функции вводим в поле Известные_значения_y диапазон ячеек C4:C11; в поле Известные_значения_х - диапазон ячеек B4:B11;
   
4. 
   чтобы вводимая формула стала формулой массива, используем комбинацию клавиш + + .
   

Введенная нами формула в строке формул будет иметь вид: ={ТЕНДЕНЦИЯ(C4:C11;B4:B11)}.

 

В результате диапазон ячеек D4:D11 заполняется соответствующими значениями функции ТЕНДЕНЦИЯ (рис. 9).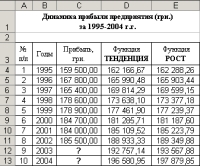

 




Для составления прогноза о прибыли предприятия на 2003 и 2004 гг. необходимо:

1. 
   выделить диапазон ячеек D12:D13, куда будут заноситься значения, прогнозируемые функцией ТЕНДЕНЦИЯ.
   
2. 
   вызвать функцию ТЕНДЕНЦИЯ и в появившемся диалоговом окне Аргументы функции ввести в поле Известные_значения_y - диапазон ячеек C4:C11; в поле Известные_значения_х - диапазон ячеек B4:B11; а в поле Новые_значения_х - диапазон ячеек B12:B13.
   
3. 
   превратить эту формулу в формулу массива, используя комбинацию клавиш Ctrl + Shift + Enter.
   
4. 
   Введенная формула будет иметь вид: ={ТЕНДЕНЦИЯ(C4:C11;B4:B11;B12:B13 )}, а диапазон ячеек D12:D13 заполнится прогнозируемыми значениями функции ТЕНДЕНЦИЯ (см. рис. 9).
   

Аналогично заполняется ряд данных с помощью функции РОСТ, которая используется при анализе нелинейных зависимостей и работает точно так же, как ее линейный аналог ТЕНДЕНЦИЯ.

 

На рис.10 представлена таблица в режиме показа формул.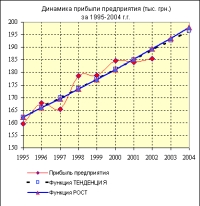

 

    

 

Для исходных данных и полученных рядов данных построена диаграмма, изображенная на рис. 11.

 

Задача 4

 

С таблицей данных о поступлении в диспетчерскую службу автотранспортного предприятия заявок на услуги за период с 1 по 11 число текущего месяца необходимо выполнить следующие действия.

1. 
   Получить ряды данных для линейной регрессии: используя функции НАКЛОН и ОТРЕЗОК; используя функцию ЛИНЕЙН.
   
2. 
   Получить ряд данных для экспоненциальной регрессии с использованием функции ЛГРФПРИБЛ.
   
3. 
   Используя вышеназванные функции, составить прогноз о поступлении заявок в диспетчерскую службу на период с 12 по 14 число текущего месяца.
   
4. 
   Для исходных и полученных рядов данных построить диаграмму.
   

Решение задачи

 

Отметим, что, в отличие от функций ТЕНДЕНЦИЯ и РОСТ, ни одна из перечисленных выше функций (НАКЛОН, ОТРЕЗОК, ЛИНЕЙН, ЛГРФПРИБ) не является регрессией. Эти функции играют лишь вспомогательную роль, определяя необходимые параметры регрессии.

 

Для линейной и экспоненциальной регрессий, построенных с помощью функций НАКЛОН, ОТРЕЗОК, ЛИНЕЙН, ЛГРФПРИБ, внешний вид их уравнений всегда известен, в отличие от линейной и экспоненциальной регрессий, соответствующих функциям ТЕНДЕНЦИЯ и РОСТ.

 

1. Построим линейную регрессию, имеющую уравнение:

 

y = mx+b


с помощью функций НАКЛОН и ОТРЕЗОК, причем угловой коэффициент регрессии m определяется функцией НАКЛОН, а свободный член b - функцией ОТРЕЗОК.

 

Для этого осуществляем следующие действия:

1. 
   заносим исходную таблицу в диапазон ячеек A4:B14;
   
2. 
   значение параметра m будет определяться в ячейке С19. Выбираем из категории Статистические функцию Наклон; заносим диапазон ячеек B4:B14 в поле известные_значения_y и диапазон ячеек А4:А14 в поле известные_значения_х. В ячейку С19 будет введена формула: =НАКЛОН(B4:B14;A4:A14);
   
3. 
   по аналогичной методике определяется значение параметра b в ячейке D19. И ее содержимое будет иметь вид: =ОТРЕЗОК(B4:B14;A4:A14). Таким образом, необходимые для построения линейной регрессии значения параметров m и b будут сохраняться соответственно в ячейках C19, D19;
   
4. 
   далее заносим в ячейку С4 формулу линейной регрессии в виде: =$C*A4+$D. В этой формуле ячейки С19 и D19 записаны с абсолютными ссылками (адрес ячейки не должен меняться при возможном копировании). Знак абсолютной ссылки $ можно набить либо с клавиатуры, либо с помощью клавиши F4, предварительно установив курсор на адресе ячейки. Воспользовавшись маркером заполнения, копируем эту формулу в диапазон ячеек С4:С17. Получаем искомый ряд данных (рис. 12). В связи с тем, что количество заявок - целое число, следует установить на вкладке Число окна Формат ячеек числовой формат с числом десятичных знаков 0.
   

2. Теперь построим линейную регрессию, заданную уравнением:

 

y = mx+b


с помощью функции ЛИНЕЙН.

 

Для этого:

1. 
   вводим в диапазон ячеек C20:D20 функцию ЛИНЕЙН как формулу массива: ={ЛИНЕЙН(B4:B14;A4:A14)}. В результате получаем в ячейке C20 значение параметра m, а в ячейке D20 - значение параметра b;
   
2. 
   вводим в ячейку D4 формулу: =$C*A4+$D;
   
3. 
   копируем эту формулу с помощью маркера заполнения в диапазон ячеек D4:D17 и получаем искомый ряд данных.
   

3. Строим экспоненциальную регрессию, имеющую уравнение:

 

y = bmx


с помощью функции ЛГРФПРИБЛ оно выполняется аналогично:

1. 
   в диапазон ячеек C21:D21 вводим функцию ЛГРФПРИБЛ как формулу массива: ={ ЛГРФПРИБЛ (B4:B14;A4:A14)}. При этом в ячейке C21 будет определено значение параметра m, а в ячейке D21 - значение параметра b;
   
2. 
   в ячейку E4 вводится формула: =$D*$C^A4;
   
3. 
   с помощью маркера заполнения эта формула копируется в диапазон ячеек E4:E17, где и расположится ряд данных для экспоненциальной регрессии (см. рис. 12).
   

 

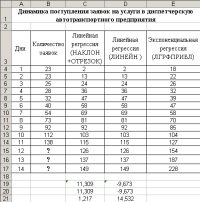На рис. 13 приведена таблица, где видны используемые нами функции с необходимыми диапазонами ячеек, а также формулы.

 

Величина R² называется коэффициентом детерминации.

Задачей построения регрессионной зависимости является нахождение вектора коэффициентов m модели (1) при котором коэффициент R принимает максимальное значение.

Для оценки значимости R применяется F-критерий Фишера, вычисляемый по формуле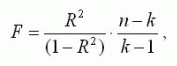



где n - размер выборки (количество экспериментов);

k - число коэффициентов модели.

 

Если F превышает некоторое критическое значение для данных n и k и принятой доверительной вероятности, то величина R считается существенной. Таблицы критических значений F приводятся в справочниках по математической статистике.

Таким образом, значимость R определяется не только его величиной, но и соотношением между количеством экспериментов и количеством коэффициентов (параметров) модели. Действительно, корреляционное отношение для n=2 для простой линейной модели равно 1 (через 2 точки на плоскости можно всегда провести единственную прямую). Однако если экспериментальные данные являются случайными величинами, доверять такому значению R следует с большой осторожностью. Обычно для получения значимого R и достоверной регрессии стремятся к тому, чтобы количество экспериментов существенно превышало количество коэффициентов модели (n>k).

Для построения линейной регрессионной модели необходимо:

1) подготовить список из n строк и m столбцов, содержащий экспериментальные данные (столбец, содержащий выходную величину Y должен быть либо первым, либо последним в списке); для примера возьмем данные предыдущего задания, добавив столбец с названием "№ периода", пронумеруем номера периодов от 1 до 12. (это будут значения Х)

 

2) обратиться к меню Данные/Анализ данных/Регрессия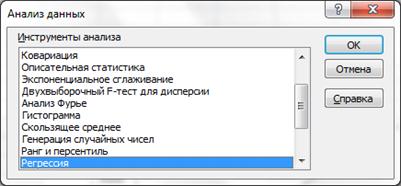



 

Если пункт "Анализ данных" в меню "Сервис" отсутствует, то следует обратиться к пункту "Надстройки" того же меню и установить флажок "Пакет анализа".

 

3) в диалоговом окне "Регрессия" задать:

·                     входной интервал Y;

·                     входной интервал X;

·                     выходной интервал - верхняя левая ячейка интервала, в который будут помещаться результаты вычислений (рекомендуется разместить на новом рабочем листе);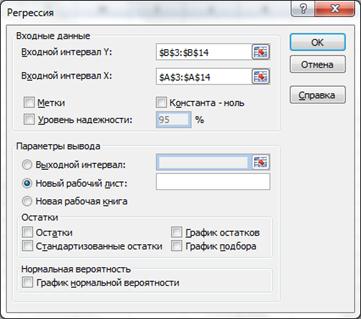

 



4) нажать "Ok" и проанализировать результаты.

 

Пример использования множественной линейной регрессии

 Предположим, что застройщик оценивает стоимость группы небольших офисных зданий в традиционном деловом районе.

Застройщик может использовать множественный регрессионный анализ для оценки цены офисного здания в заданном районе на основе следующих переменных.

y - оценочная цена здания под офис;

x₁ - общая площадь в квадратных метрах;

x₂ - количество офисов;

x₃ - количество входов (0,5 входа означает вход только для доставки корреспонденции);

x₄ - время эксплуатации здания в годах.

 

В этом примере предполагается, что существует линейная зависимость между каждой независимой переменной (x₁, x₂, x₃ и x₄) и зависимой переменной (y), то есть ценой здания под офис в данном районе. Исходные данные показаны на рисунке.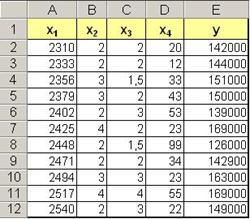

 



 

Настройки для решения поставленной задачи показаны на рисунке окна "Регрессия". Результаты расчетов размещены на отдельном листе в трех таблицах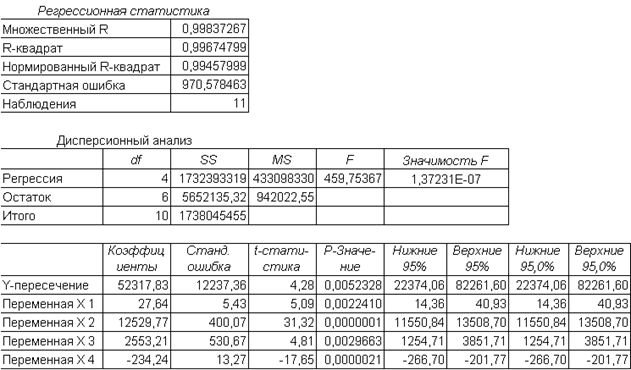

 



 

В итоге мы получили следующую математическую модель:

y = 52318 + 27,64*x₁ + 12530*x₂ + 2553*x₃ - 234,24*x₄.

Теперь застройщик может определить оценочную стоимость здания под офис в том же районе. Если это здание имеет площадь 2500 квадратных метров, три офиса, два входа и время эксплуатации - 25 лет, можно оценить его стоимость, используя следующую формулу:

y = 27,64*2500 + 12530*3 + 2553*2 - 234,24*25 + 52318 = 158 261 у.е.