Главная страница
Навигация по странице:

  • Решение 1.

  • Задача 4 Решение

    		•

    задачи предпринимательство. Задача 1 Имеются данные об урожайности зерновых в хозяйствах в области


    Скачать 270.77 Kb.
    НазваниеЗадача 1 Имеются данные об урожайности зерновых в хозяйствах в области
    Анкорзадачи предпринимательство
    Дата14.11.2022
    Размер270.77 Kb.
    Формат файлаdocx
    Имя файла1.docx
    ТипЗадача
    #788574
    страница1 из 3
      1   2   3

    Задача 1

    Имеются данные об урожайности зерновых в хозяйствах в области

    Год
    Урожайность ц/га

    1
    10,2

    2
    10,7

    3
    11,7

    4
    13,1

    5
    14,9

    6
    17,2

    7
    20,0

    8
    23,2


    Задание:

    1. Обоснуйте выбор типа уравнения тренда.

    2. Рассчитайте параметры уравнения тренда.

    3. Дайте прогноз урожайности зерновых на следующий год.
    Решение:




    Изучив график, становится ясно, что наилучшим образом аппроксимирует имеющиеся данные прямая линия. Именно поэтому тип уравнения тренда – линейная функция.

    3. Параметры трендов определяются МНК, в качестве независимой переменной выступает время t=1,2,…,8, а в качестве зависимой переменной – фактические уровни временного ряда yt. Расчет параметров a и b уравнения регрессии производится по формулам: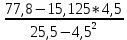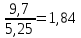

    =

    15,125-1,84*4,5= 6,84


     
    X
    Y
    Y*X
    X^2

     
    1
    10,2
    10,2
    1

     
    2
    10,7
    21,4
    4

     
    3
    11,7
    35,1
    9

     
    4
    13,1
    52,4
    16

     
    5
    14,9
    74,5
    25

     
    6
    17,2
    103,2
    36

     
    7
    20
    140
    49

     
    8
    23,2
    185,6
    64

    сумма
    36
    121
    622,4
    204

    среднее значение
    4,5
    15,125
    77,8
    25,5

    Таким образом, уравнение линейной регрессии имеет вид: y = 6,84+1,84х .

    4.Исходя из значения параметра b=1,84, можно предположить, что урожайность культур на следующий год увеличится на 1,8%.
    Задача 2

    По данным за 30 месяцев некоторого временного ряда х1 были получены значения коэффициентов автокорреляции уровней:

    r1 = 0,63;

    r2 = 0,38;

    r3 = 0,72;

    r4 = 0,97;

    r5 = 0,55;

    r6 = 0,40;

    r7 = 0,65

    rt - коэффициенты автокорреляции i-го порядка.

    Требуется:

    1.Охарактеризовать структуруэтого ряда, используя графическое изображение.

    2.Для прогнозирования значений xt в будущие периоды предполагается построить уравнение авторегрессии. Выбрать наилучшее уравнение, обосновать выбор. Указать общий вид этого уравнения.
    Решение

    1. Так как значения всех коэффициентов автокорреляции достаточно высокие, ряд содержит тенденцию. Поскольку наибольшее абсолютное значение имеет коэффициент автокорреляции 4-го порядка r 4, ряд содержит периодические колебания, цикл этих колебаний равен 4.

    График этого ряда можно представить на рис. 1.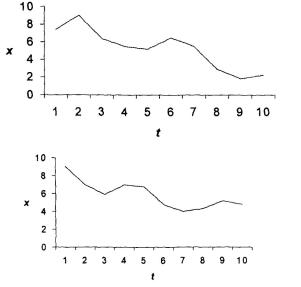



    Рис. 1. Графики, характеризующие убывающую тенденцию при разных возможных периодических колебаниях

    2. Наиболее целесообразно построение уравнения авторегрессии:

    уt = а + b ∙ уt-4 + иt ,

    так как значение r 4 = 0,97 свидетельствует о наличии очень тесной связи между уровнями ряда с лагом в 4 месяца.

    Кроме того, возможно построение и множественного уравнения авторегрессии уt от уt-3 и уt-4 так как r4 = 0,72:

    уt, = а + b1 ∙ уt-3 +b2 ∙ уt-4 + иt,

    Сравнить полученные уравнения и выбрать наилучшее решение можно с помощью скорректированного коэффициента детерминации.
    Задача 3

    Пусть имеется следующий временной ряд:

    T
    1
    2
    3
    4
    5
    6
    7
    8

    Xt
    20
    …
    …
    …
    …
    …
    …
    10

    Известно также, что  ,  ,  .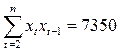

    Задание:

    1. Определите коэффициент автокорреляции уровней этого ряда первого порядка.

    2. Установите, включает ли исследуемый временной ряд тенденцию.

    Решение

    Значение коэффициента определим по формуле: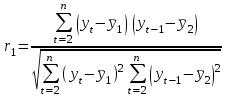



    Распишем все компоненты этой формулы. Числитель преобразуем следующим путем: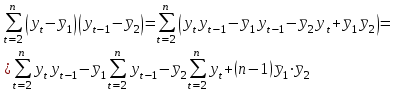



    Здесь n=8 значения средних вычисляем по соответствующим формулам; при этом значения сумм рассчитываются с учетом крайних значений временного ряда: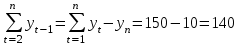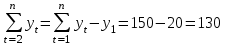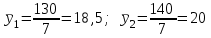







    Отсюда: +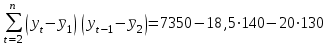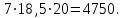

    Аналогично рассчитываем каждый член в знаменателе: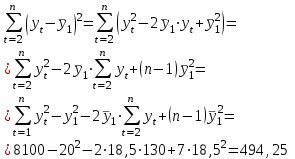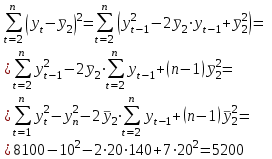





    Результат определим по исходной расчетной формуле: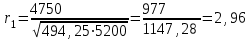


    Задача 4
    Решение:


    1. Сведем промежуточные расчеты в таблицу 1.

    Таблица 1 Расчет коэффициента автокорреляции первого порядка для временного ряда уровня безработицы

    t
    x
    y
    x2
    y2
    x•y

    2
    8,8
    8,6
    77,44
    73,96
    75,68

    3
    8,6
    8,4
    73,96
    70,56
    72,24

    4
    8,4
    8,1
    70,56
    65,61
    68,04

    5
    8,1
    7,9
    65,61
    62,41
    63,99

    6
    7,9
    7,6
    62,41
    57,76
    60,04

    7
    7,6
    7,4
    57,76
    54,76
    56,24

    8
    7,4
    7,9
    54,76
    62,41
    58,46

    Итого
    56,8
    55,9
    462,5
    447,47
    454,69

    Рассчитаем выборочные средние:







    Выборочные дисперсии составят:





    Среднеквадратические отклонения равны:





    Линейный коэффициент автокорреляции rt,t-1 рассчитывается по формуле:



    Таким образом, рассчитанный коэффициент автокорреляции показывает, что связь между уровнями безработицы текущего и непосредственно предыдущего месяцев весьма высокая и прямая (0,9 < rt,t-1 < 1), т.е. во временном ряде уровня безработицы имеется тенденция.

    Рассчитаем коэффициента автокорреляции 2-го порядка (таблица 2).

    Таблица 2 Расчет коэффициента автокорреляции второго порядка для временного ряда уровня безработицы

    t
    x
    y
    x2
    y2
    x•y

    3
    8,8
    8,4
    77,44
    70,56
    73,92

    4
    8,6
    8,1
    73,96
    65,61
    69,66

    5
    8,4
    7,9
    70,56
    62,41
    66,36

    6
    8,1
    7,6
    65,61
    57,76
    61,56

    7
    7,9
    7,4
    62,41
    54,76
    58,46

    8
    7,6
    7,9
    57,76
    62,41
    60,04

    Итого
    49,4
    47,3
    407,74
    373,51
    390

    Вычислим выборочные средние:







    Определим выборочные дисперсии:





    Среднеквадратические отклонения составят:





    Линейный коэффициент автокорреляции rt,t-1 рассчитывается по формуле:



    Таким образом, рассчитанный коэффициент автокорреляции показывает, что связь между уровнями безработицы текущего и непосредственно предыдущего месяцев заметная и прямая (0,7 < rt,t-1 < 1), т.е. во временном ряде уровня безработицы имеется тенденция.

    Т.е. проведенные расчеты показывают, что ряд содержит тенденцию.
      1   2   3

    написать администратору сайта