задачи предпринимательство. Задача 1 Имеются данные об урожайности зерновых в хозяйствах в области

• Название: Задача 1 Имеются данные об урожайности зерновых в хозяйствах в области
• Анкор: задачи предпринимательство
• Дата: 14.11.2022
• Размер: 270.77 Kb.
• Имя файла: 1.docx
• Тип: Задача; #788574
• страница: 2 из 3

Задача 5

 Годовое потребление некоторого товара и доходы населения (тыс. руб.) за 1989-1997 гг. приведены в таблице:

Годы	1	2	3	4	5	6	7	8	9
Потребление	46	50	54	59	62	67	75	86	100
Доходы	53	57	64	70	73	82	95	110	127

Задание: Построить уравнение регрессии, включив в него фактор времени, если известно, что  599, 731, 52179, 64361, 42367.
Решение:
Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор s получается из выражения: s = (X^TX)^-1X^TY
К матрице с переменными X_j добавляем единичный столбец:


Матрица X^T

1	1	1	1	1	1	1	1	1
46	50	54	59	62	67	75	86	100
53	57	64	70	73	82	95	110	127

Умножаем матрицы, (X^TX)

XT X =

9 599 731 599 42367 52179 731 52179 64361

В матрице, (X^TX) число 9, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X^T и 1-го столбца матрицы X
Умножаем матрицы, (X^TY)

XT Y =

45 3369 4184

Находим обратную матрицу (X^TX)^-1

(XT X) -1 =

14,794 -1,4649 1,0196 -1,4649 0,1606 -0,1136 1,0196 -0,1136 0,08052

Вектор оценок коэффициентов регрессии равен

Y(X) =

14,794 -1,4649 1,0196 -1,4649 0,1606 -0,1136 1,0196 -0,1136 0,08052

*

45 3369 4184

=

-3,5036 -0,01219 0,1147

Уравнение регрессии (оценка уравнения регрессии)
Y = -3.5036-0.01219X₁ + 0.1147X₂
Интерпретация коэффициентов регрессии. Константа оценивает агрегированное влияние прочих (кроме учтенных в модели х_i) факторов на результат Y и означает, что Y при отсутствии x_i составила бы -3.5036. Коэффициент b₁ указывает, что с увеличением x₁ на 1, Y снижается на 0.01219. Коэффициент b₂ указывает, что с увеличением x₂ на 1, Y увеличивается на 0.1147.
2. Матрица парных коэффициентов корреляции R.
Число наблюдений n = 9. Число независимых переменных в модели равно 2, а число регрессоров с учетом единичного вектора равно числу неизвестных коэффициентов. С учетом признака Y, размерность матрицы становится равным 4. Матрица, независимых переменных Х имеет размерность (9 х 4).
Матрица A, составленная из Y и X

1	1	46	53
1	2	50	57
1	3	54	64
1	4	59	70
1	5	62	73
1	6	67	82
1	7	75	95
1	8	86	110
1	9	100	127

Транспонированная матрица.

1	1	1	1	1	1	1	1	1
1	2	3	4	5	6	7	8	9
46	50	54	59	62	67	75	86	100
53	57	64	70	73	82	95	110	127

Матрица X^TX.

9	45	599	731
45	285	3369	4184
599	3369	42367	52179
731	4184	52179	64361

Полученная матрица имеет следующее соответствие:

∑n	∑y	∑x1	∑x2
∑y	∑y2	∑x1 y	∑x2 y
∑x1	∑yx1	∑x1 2	∑x2 x1
∑x2	∑yx2	∑x1 x2	∑x2 2

Найдем парные коэффициенты корреляции.


Значения парного коэффициента корреляции свидетельствует о весьма сильной линейной связи между x₁ и y.

Значения парного коэффициента корреляции свидетельствует о весьма сильной линейной связи между x₂ и y.

Значения парного коэффициента корреляции свидетельствует о весьма сильной линейной связи между x₂ и x₁.

Признаки x и y	∑xi		∑yi		∑xi*yi
Для y и x1	599	66.556	45	5	3369	374.333
Для y и x2	731	81.222	45	5	4184	464.889
Для x1 и x2	731	81.222	599	66.556	52179	5797.667

Дисперсии и среднеквадратические отклонения.

Признаки x и y
Для y и x1	277.802	6.667	16.667	2.582
Для y и x2	554.173	6.667	23.541	2.582
Для x1 и x2	554.173	277.802	23.541	16.667

Матрица парных коэффициентов корреляции R:

-	y	x1	x2
y	1	0.9656	0.967
x1	0.9656	1	0.9988
x2	0.967	0.9988	1

Рассчитаем наблюдаемые значения t-статистики для r_yx1 по формуле:

где m = 1 - количество факторов в уравнении регрессии.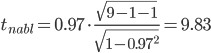

По таблице Стьюдента находим Tтабл
t_крит(n-m-1;α/2) = (7;0.025) = 2.841
Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим
Рассчитаем наблюдаемые значения t-статистики для r_yx2 по формуле:

Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим