Практическая работа 1 По дисциплине Статистические методы интеллектуального анализа данных
 Скачать 148.84 Kb. Скачать 148.84 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Пермский национальный исследовательский политехнический университет» Кафедра микропроцессорных средств автоматизации ПРАКТИЧЕСКАЯ РАБОТА №1 По дисциплине: «Статистические методы интеллектуального анализа данных» Выполнил: студент гр. ИСУП-20-1м Гоголевский И.В. Проверил: доцент Мыльников Л.А. Пермь 2021 Задание: Выбрать данные из источников, предложенных на лекции; Обработать данные с помощью R-studio; Рассчитать коэффициенты аппроксимирующего полинома методом наименьших квадратов на первых 2/3 заданного диапазона; Произвести экстраполяцию, используя полученные коэффициенты, на оставшуюся 1/3 диапазона; Произвести оценку адекватности модели используя один из критериев; Произвести сравнение исходного графика функции и аппроксимированного. Ход работы: Выберем данные для выполнения работы с портала https://github.com 1.1 Для выполнения работы выберем набор данных из раздела Энергетика: «Данные о почасовом потреблении энергии и температуре наружного воздуха для 11 коммерческих зданий (офисы / магазины)» Сохраним данные в формате .csv. Данные сортированы по следующим столбцам: - Дата и время мониторинга - Температура наружного воздуха в F - Мощность потребляемая зданием в кВт Для проведения работы выберем столбец Power..kW. Запустим R-studio и считаем данные из файла. Зададимся первыми 2/3диапазона. 2.1 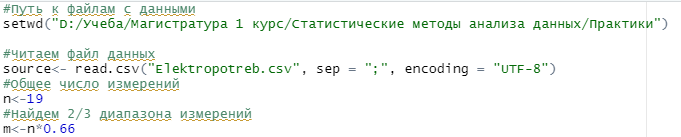 Выведем на график значения x1 (первые 2/3 диапазона) Выделяем набор данных, для которого будем строить регрессионную модель, получаем коэффициенты, строим функцию от x1, выводим на график. 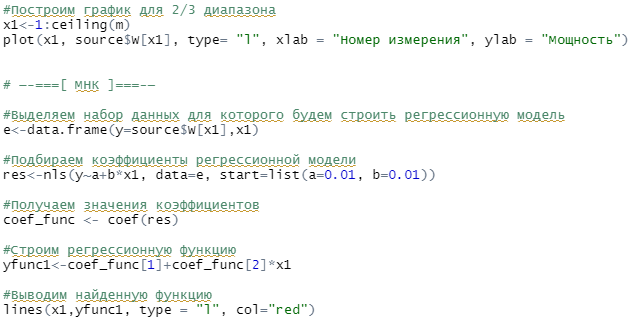 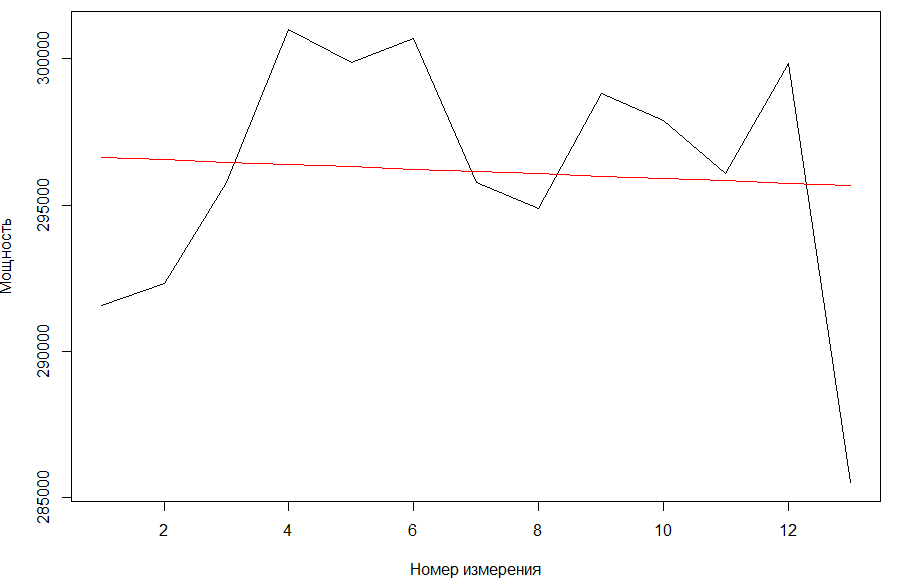 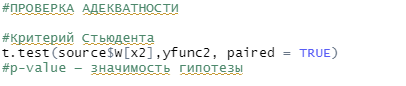 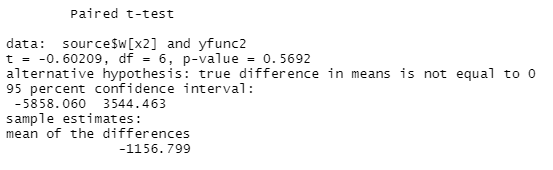 Т.к. p-value=0,5692, то гипотеза значима. Найдем третью часть диапазона значений, обозначим ее как x2. Используя полученные коэффициенты, экстраполируем функцию. Выведем все получившиеся функции на график.  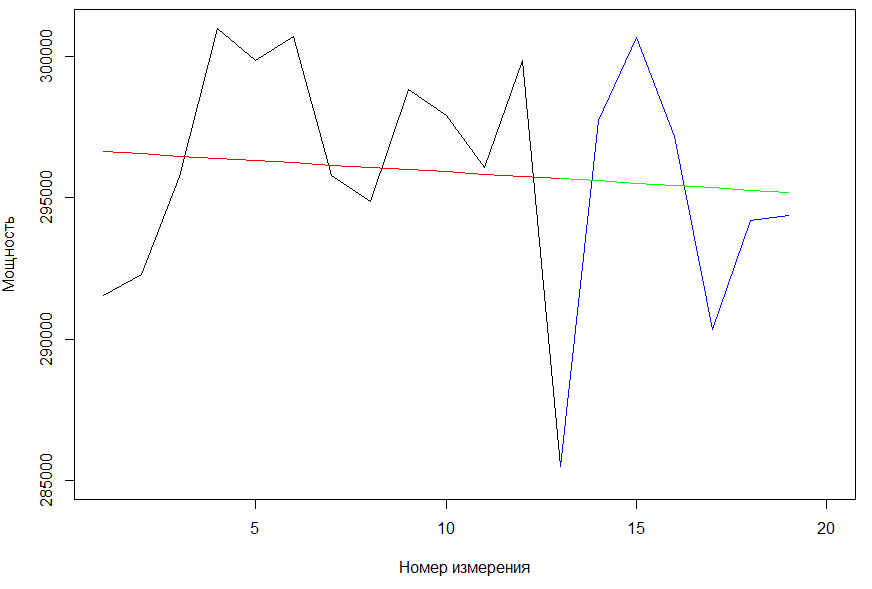 Выводы При экстраполировании исходного графика функции методом наименьших квадратов удалось добиться наилучшей аппроксимации (аппроксимирующая функция лежит максимально близко к исходным узлам). В качестве аппроксимирующей была выбрана линейная функция вида: y=a0+b*x. Также можно сделать вывод, что метод наименьших квадратов плохо подходит для экстраполирования функций, скачкообразно изменяющихся в экстраполируемой области. |
